Подібность при вивченні теми «Геометричні перетворення».
ВІННИЦЬКИЙ ДЕРЖАВНИЙ ПЕДАГОГІЧНИЙ УНІВЕРСИТЕТ
ІМЕНІ МИХАЙЛА КОЦЮБИНСЬКОГО
Інститут математики, фізики та технологічної освіти
Кафедра математики і методики навчання математики
Вивчення подібності в основній школі

Вінниця 2012
Упорядник:
Назаренко А.Л . – студентка напряму підготовки Математика освітньо-кваліфікаційного рівня «Бакалавр» Вінницького державного педагогічного університету імені Михайла Коцюбинського
Рецензенти:
Матяш О.І. – кандидат педагогічних наук, доцент кафедри
математики і методики навчання математики Вінницького державного педагогічного університету імені Михайла Коцюбинського
Коношевський О.Л. – кандидат педагогічних наук, доцент кафедри математики і методики навчання математики Вінницького державного педагогічного університету імені Михайла Коцюбинського
Посібник підготовлений на допомогу вчителям математики та студентам математичних спеціальностей педагогічних університетів. Мета посібника: допомогти вчителю, особливо молодому, якомога ефективніше організовувати, здійснювати і контролювати навчальні процеси при вивченні подібності в основній школі.
Затверджено на засіданні кафедри математики і
методики навчання математики
(протокол №3 від 25.04.12)
ЗМІСТ
1. Введення поняття подібності трикутників в шкільному курсі планіметрії
2. Доведення класичних теорем планіметрії за допомогою перетворень подібності
3. Властивості трапеції, які доводяться за допомогою подібності трикутників
4. Задачі прикладного змісту при вивченні подібності трикутників в основній школі
5. Методика розв’язування задач на побудову методом подібності в шкільному курсі математики
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
ПЕРЕДМОВА
Перетворення подібності – один із провідних методів сучасної математики, який широко застосовується в шкільному курсі планіметрії для доведення різноманітних теорем, розв’язування задач.
Вивчення перетворення подібності сприяє всебічному розвитку школярів, зокрема, розвитку логічного мислення, просторової уяви, математичної ініціативи. Подібність використовується при визначенні відстаней до недоступних предметів, при визначенні глибини ставка або колодязя, в пристроях різних вимірювальних інструментів та приладів, тощо.
Подібність розглядається у шкільному курсі геометрії двічі – у 8 класі при вивченні теми «Подібність трикутників» та у 9 при вивченні теми «Геометричні перетворення». Ця тема для учнів є дещо важчою у порівнянні із попередніми темами шкільної планіметрії, то у даному посібнику ми детально зупинилися на: введенні поняття подібних трикутників в курсі планіметрії основної школи, задачах прикладного змісту при вивченні подібності трикутників та методиці розв’язування задач на побудову методом подібності.
1. Введення поняття подібності трикутників в шкільному курсі планіметрії
У методиці навчання математики важливе значення приділяють введенню математичних понять. Багато вчителів вважають, що процес формування поняття під час уроку має бути спрямований на розуміння інформації шляхом сприймання і осмислення поняття у всіх його проявах і взаємозв’язках. Така системність знань вже на етапі первісного опрацювання виявляється у здатності учня розрізняти суттєві і несуттєві ознаки поняття, бачити можливості для узагальнення й обмеження, виявляти його місце у системі математичних понять.[7]
Також вчителі вважають, що введення математичного поняття повинно сприяти набуттю учнями практичних навичок, тому варто не стільки мотивувати власне поняття чи необхідність його вивчення, скільки забезпечити умови для творчої навчально-пізнавальної праці учнів, стимулювати їх особисту зацікавленість у засвоєнні знань, створювати робочий настрій.
У методичній літературі питанню введення математичних понять приділяли увагу Бевз Г. П., Гришина Т.А., Слєпкань З.І., Тализіна Н. Ф., Фрідман Л.М. та інші.
Зокрема З.І. Слєпкань чітко виділила основні етапи введення математичних понять конкретно-індуктивним та абстрактно-дедуктивним методами. Введення поняття конкретно-індуктивним методом передбачає: аналіз конкретних прикладів, дібраних вчителем, серед яких повинні бути як об’єкти, що належать даному поняттю, так і ті що не належать йому; вводення терміну; виявлення суттєвих властивостей поняття; з’ясування несуттєвих властивостей поняття, що формулюються; формулювання означення поняття; розгляд вправ на підведення під поняття. Введення поняття абстрактно-дедуктивним методом завбачує: формулювання означення поняття; розгляд прикладів об’єктів, що належать даному поняттю; аналіз означення, виявлення суттєвих і несуттєвих властивостей поняття; розгляд вправ на підведення під поняття та виведення наслідків.[10]
Г.П. Бевз зазначає для того, щоб означення були правильними вони повинні задовольняти такі правила: 1) означення повинно бути відповідним означуваному поняттю; 2) означення не повинно містити ще не означених понять; 3) означення не повинні суперечити одне одному; 4) означення по можливості не повинно містити нічого зайвого.[3]
Т. А. Гришина пропонує своє бачення введення геометричних понять, зокрема, нею було виділено 4 кроки введення поняття: 1) номінація поняття – його назва, найменування, зображення на площині, введення нової термінології та символіки; 2) інтерпретація поняття – роз’яснення його змісту: виділення суттєвих ознак, установлення родо-видових зв’язків; 3) екстраполяція поняття – поширення висновків, одержаних на попередньому етапі, на всю сукупність споріднених понять, розкриття цього обсягу; 4) ідентифікація поняття – уподібнення поняття, узагальнення критеріїв його розпізнавання для підведення об’єкта під поняття.[7]
Зрозуміло, що у щоденній підготовці до уроків, не завжди можна виділити всі перераховані етапи. Вважаємо для коректного введення математичного поняття слід виділяти три основні етапи:
формулювання означення поняття;
розгляд прикладів об’єктів, що належать даному поняттю;
виявлення суттєвих та з’ясування несуттєвих властивостей поняття.
У залежності від підготовки учнів, від матеріалу, що вивчається, послідовність цих етапів може змінюватись.
Відповідно до діючих програм з геометрії поняття подібних трикутників вводиться у 8 класі. Учні повинні засвоїти означення подібних трикутників та їх ознаки, навчитися застосовувати вивчені знання на практиці. Отже, в межах теми «Подібність трикутників» розглядаються такі нові поняття: подібні фігури та подібні трикутники.
Зокрема, у підручнику авторського колективу Мерзляк А.Г. та інші «Геометрія 8» [9] поняття подібних трикутників вводиться таким чином: два трикутники називаються подібними, якщо у них рівні кути і відповідні сторони пропорційні.
У підручниках з геометрії для 8 класу авторів Бевз Г.П. та інші [2], Єршов С.В.[8] підхід до введення цих понять практично такий самий: спочатку описується поняття подібних фігур, потім означається поняття подібних трикутників.
У підручнику «Геометрія 8» авторського колективу Бурда М.І., Тарасенкова Н.А. [5] на конкретних прикладах двох подібних трикутників означається поняття подібність трикутників. Поняття подібні фігури тут не розглядається.
У підручнику з геометрії для 8 класу Апостолової Г.В.[1] параграф «Подібність трикутників» починається із означення, яке формулюється таким чином: два трикутники називаються подібними, якщо в них рівні кути, а проти рівних кутів лежать пропорційні сторони. Хоча означення із підручника [1] є тотожно сформульованим у попередніх авторів, однак доступнішим і кращим для сприйняття учнями вважаємо означення, яке сформульовано у підручниках [2], [5], [8], [9].
При введенні поняття подібних трикутників в курсі планіметрії основної школи спочатку потрібно сформувати в учнів поняття подібних фігур, розібравшись з подібністю у реальному і в повсякденному житті. Наочність полегшує сприйняття математичних понять, сприяє утворенню ясних і точних образів. На рисунках 1 - 4 наведено приклади подібних трикутників, які зустрічаються у нашому житті.


Кафедральний Собор в Сієні Сіднейський оперний театр
Рис.1. Рис.2.


Англійська архітектура Зуби акули
Рис.3. Рис.4.
Далі використаємо малюнок двох подібних трикутників з позначенням рівності кутів (рис.5) і запропонуємо інший запис з використанням буквеної символіки. Таким чином, подібність трикутників означається через рівність кутів та пропорційності відповідних сторін. Нехай ![]() ~
~![]() тоді
тоді ![]() і
і 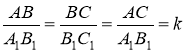 . З останньої рівності випливає поняття коефіцієнта подібності.
. З останньої рівності випливає поняття коефіцієнта подібності.
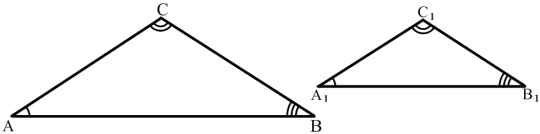
Рис.5.
Потім доцільно сформулювати означення: два трикутники називаються подібними, якщо у них рівні кути і відповідні сторони пропорційні.
На уроці, працюючи з учнями, при введенні нового поняття, перш за все потрібно з’ясувати структурні зв’язки означуваного поняття з раніше вивченими. При вивченні подібних трикутників ми знаємо, що у попередніх класах вивчались рівні трикутники і учні добре засвоїли цю тему, їм відомо, що рівними трикутниками називають трикутники, якщо їх відповідні елементи рівні. А при введенні терміну подібних трикутників потрібно наголосити на властивостях, які притаманні лише цьому терміну. У нашому випадку увага звертається на те, що кути у трикутників рівні і відповідні сторони пропорційні, а те що трикутники матимуть різні розміри – це лише урізноманітнює загальний вигляд фігури.
Після введення поняття подібності трикутників доцільно навести найпростіші приклади на застосування цього поняття. Закріпити дане означення за допомогою специфічних вправ, використовуючи наочність. Для прикладу можна запропонувати такі завдання:
1) а) Виріжте з паперу чотири рівні трикутники.
б) Один з них залиште без змін, а від інших відріжте частини, що відтинаються середніми лініями, паралельними кожній із сторін (рис.6).
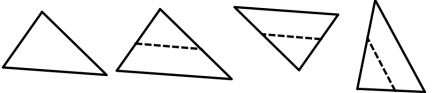
Рис.6.
в) Порівняйте кути трьох отриманих трикутників із кутами першого трикутника. Зробіть висновок.
г) Виміряйте довжини сторін двох утворених трикутників. Порівняйте відношення довжин їх відповідних сторін. Зробіть висновок.
Зрозуміло, що якщо учні виконають це завдання то вони усвідомлять саме означення подібних трикутників. Адже це все вже було перевірено ними на практиці, і дане поняття залишиться в їхній пам’яті на довгий строк.
2) З нижче наведених трикутників виберіть зайвий:
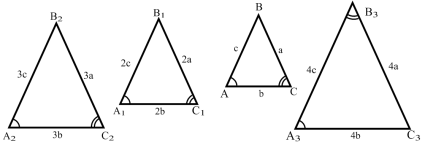
Рис. 7.
3) З наведених нижче трикутників виберіть пари подібних трикутників:
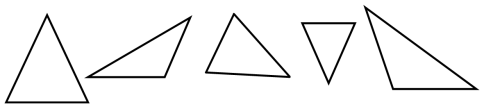
Рис.8.
4) Чи подібні трикутники зображені на рисунку 9? Якщо так, то назвіть їх відповідні кути і відповідні сторони.
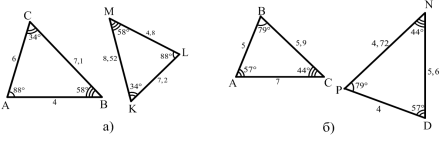
Рис.9.
5) На рисунку 10 зображено подібні трикутники ![]() і
і![]() , рівні кути яких позначено однаковою кількістю дуг. Запишіть пропорційні сторони цих трикутників.
, рівні кути яких позначено однаковою кількістю дуг. Запишіть пропорційні сторони цих трикутників.
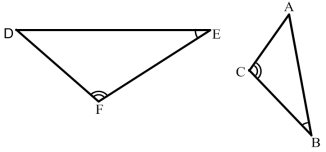
Рис.10.
Правильно виконуючи усні вправи закріплюється вивчений матеріал і виробляються навички розв’язування вправ.
Отже, ми продемонстрували процес формування поняття подібні трикутники в курсі геометрії 8 класу. Слід відмітити, що перш ніж розпочати введення цього поняття, потрібно розглянути поняття подібних фігур. А при поясненні матеріалу, що стосується даної теми доречно звернути увагу на суттєві та несуттєві властивості поняття. Після цього закріпити вивчений матеріал на практиці.
2. Доведення класичних теорем планіметрії за допомогою перетворень подібності
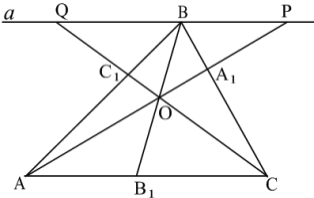
Теорема 1. (Теорема Чеви). На сторонах ![]() ,
, ![]() і
і ![]() трикутника
трикутника ![]() взято відповідні точки
взято відповідні точки ![]() ,
, ![]() і
і ![]() . Для того щоб відрізки
. Для того щоб відрізки ![]() перетиналися в одній точці (рис. 11), необхідно й достатньо, щоб виконувалась рівність Рис. 11
перетиналися в одній точці (рис. 11), необхідно й достатньо, щоб виконувалась рівність Рис. 11
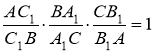 . (1)
. (1)
Доведення. Необхідність. Доведемо, що три відрізка ![]() ,
, ![]() і
і ![]() перетинаються в точці О, тоді виконується рівність (1). Проведемо через вершину В пряму
перетинаються в точці О, тоді виконується рівність (1). Проведемо через вершину В пряму ![]() . Нехай прямі
. Нехай прямі ![]() , і
, і ![]() перетинають пряму
перетинають пряму ![]() в точках P і Q відповідно. Тоді із подібності трикутників
в точках P і Q відповідно. Тоді із подібності трикутників ![]() і
і ![]() маємо:
маємо:
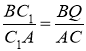 (2)
(2)
Аналогічно із ![]() маємо:
маємо: 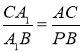 (3).
(3).
Із ![]() (точніше, із-за їх гомотетичності) маємо:
(точніше, із-за їх гомотетичності) маємо:
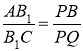 (4).
(4).
Перемноживши відповідно, ліві і праві частини рівностей (2), (3), (4),
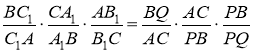 .
.
Отримаємо 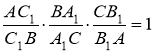 .
.
 Достатність. Якщо виконується умова (1) то відрізки
Достатність. Якщо виконується умова (1) то відрізки ![]() ,
, ![]() і
і ![]() перетинаються в одній точці
перетинаються в одній точці ![]() .
.
Нехай відрізки ![]() і
і ![]() перетинаються в точці
перетинаються в точці ![]() , а відрізок, який проходить через вершину
, а відрізок, який проходить через вершину ![]() і точку
і точку ![]() перетинає сторону
перетинає сторону ![]() у деякій точці
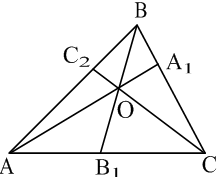
у деякій точці ![]() (рис. 12). З доведеного вище можна записати:
(рис. 12). З доведеного вище можна записати:
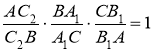 . Рис. 12
. Рис. 12
Зіставляючи цю рівність з рівністю (1), доходимо висновку, що 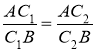 , тобто точки
, тобто точки ![]() і
і ![]() ділять відрізок
ділять відрізок ![]() в одному й тому самому відношенні, а отже, ці точки збігаються. Звідси випливає, що пряма
в одному й тому самому відношенні, а отже, ці точки збігаються. Звідси випливає, що пряма ![]() перетинає сторону
перетинає сторону ![]() у точці
у точці ![]() .
.
Теорема 2. (Теорема Менелая). На сторонах ![]() і
і ![]() трикутника
трикутника ![]() взято відповідні точки
взято відповідні точки ![]() і
і ![]() , а на продовженні сторони
, а на продовженні сторони ![]() - точку
- точку ![]() . Для того щоб точки
. Для того щоб точки ![]() лежали на одній прямій, необхідно й достатньо, щоб виконувалась рівність
лежали на одній прямій, необхідно й достатньо, щоб виконувалась рівність
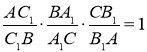 . (1)
. (1)
Доведення. Спочатку доведемо необхідну умову колінеарності: якщо точки ![]() лежать на одній прямій то виконується рівність (1).
лежать на одній прямій то виконується рівність (1).
З вершин трикутника ![]() опустимо перпендикуляри
опустимо перпендикуляри ![]() і
і ![]() на пряму
на пряму ![]() (рис. 13). Оскільки
(рис. 13). Оскільки ![]() , то
, то ![]() ~
~![]() за першою ознакою подібності трикутників. Звідси
за першою ознакою подібності трикутників. Звідси 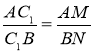 . З подібності
. З подібності 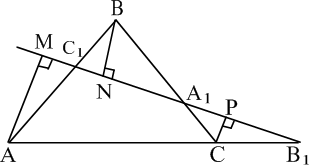 трикутників
трикутників ![]() і
і ![]() отримуємо, що
отримуємо, що 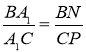 .
.
З подібності трикутників ![]() і
і ![]() маємо рівність
маємо рівність 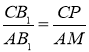 . З трьох отриманих пропорцій випливає, що Рис. 13
. З трьох отриманих пропорцій випливає, що Рис. 13
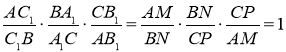 .
.
Тепер доведемо достатню умову колінеарності: якщо виконується рівність (1), то точки ![]() лежать на одній прямій.
лежать на одній прямій.
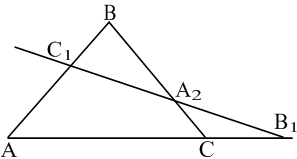 Нехай
Нехай ![]() перетинає сторону
перетинає сторону ![]() трикутника
трикутника ![]() у деякій точці
у деякій точці ![]() (рис. 14). З доведеного вище можна записати:
(рис. 14). З доведеного вище можна записати: 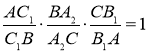 . Зіставляючи цю рівність з рівністю (1), доходимо висновку, що
. Зіставляючи цю рівність з рівністю (1), доходимо висновку, що  , Рис. 14
, Рис. 14
тобто точки ![]() і
і ![]() поділяють відрізок
поділяють відрізок ![]() в одному й тому самому відношенні, а отже, ці точки збігаються. Звідси випливає, що пряма
в одному й тому самому відношенні, а отже, ці точки збігаються. Звідси випливає, що пряма ![]() перетинає сторону
перетинає сторону ![]() у точці
у точці ![]() .[9]
.[9]
Теорема 3. (Теорема Птолемея). Добуток діагоналей вписаного чотирикутника дорівнює сумі добутків його протилежних сторін.
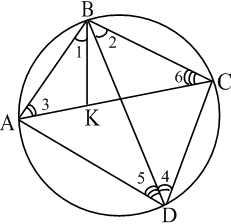 Доведення. На діагоналі
Доведення. На діагоналі ![]() вписаного чотирикутника
вписаного чотирикутника ![]() (рис.15) візьмемо точку
(рис.15) візьмемо точку ![]() таку, що
таку, що ![]() Тоді
Тоді ![]() за першою ознакою подібності трикутників (
за першою ознакою подібності трикутників (![]() , як вписані, що спираються на одну й ту саму дугу). Звідси
, як вписані, що спираються на одну й ту саму дугу). Звідси ![]() , тобто
, тобто
![]() (1)
(1)
Зрозуміло, що ![]() . Також
. Також ![]() , як вписані, що спираються на одну й ту саму дугу. Рис. 15
, як вписані, що спираються на одну й ту саму дугу. Рис. 15
Тому ![]() . Звідси
. Звідси ![]() , тобто
, тобто ![]() (2)
(2)
Додавши рівності (1) і (2) отримуємо:
![]() , тобто
, тобто
![]() , звідси
, звідси
![]() .
.
Теорему доведено.[9]
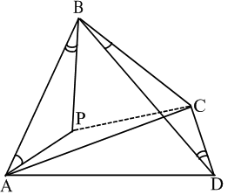 Теорема 4. (Нерівність Птолемея). Для опуклого чотирикутника
Теорема 4. (Нерівність Птолемея). Для опуклого чотирикутника ![]() виконується нерівність
виконується нерівність ![]() .
.
Рівність досягається тоді і тільки тоді, коли чотирикутник ![]() можна вписати в коло.
можна вписати в коло.
Доведення. Проведемо через вершини ![]() і
і ![]() чотирикутника
чотирикутника ![]() такі промені
такі промені ![]() та
та ![]() , щоб
, щоб ![]() , а
, а ![]() Рис. 16
Рис. 16
(рис. 16). ![]() ,
, ![]()
![]()
Звідси ![]() .
.
![]() , тому,
, тому, ![]() , тобто
, тобто ![]() .
.
За нерівністю трикутника ![]() . Тому
. Тому ![]() . Звідси випливає нерівність
. Звідси випливає нерівність ![]() , що і треба було довести. Знак рівності буде лише тоді, коли точка
, що і треба було довести. Знак рівності буде лише тоді, коли точка ![]() лежить на відрізку
лежить на відрізку ![]() . Але тоді
. Але тоді ![]() тобто точки
тобто точки ![]() лежать на одному колі.[11]
лежать на одному колі.[11]
Теорема 5. (Теорема Ван-Обеля). Якщо ![]() - точки, які лежать на сторонах
- точки, які лежать на сторонах ![]() довільного трикутника
довільного трикутника ![]() так, що відрізки (чевіани)
так, що відрізки (чевіани) ![]() перетинаються в одній точці
перетинаються в одній точці ![]() , то ця точка ділить відрізок
, то ця точка ділить відрізок ![]() у відношенні:
у відношенні:
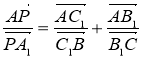 . (1)
. (1)
Також виконуються аналогічні рівності, які відповідають чевіанам ![]() і
і ![]() .
.
Доведення. Нехай ![]() задовольняє умови теореми.
задовольняє умови теореми.
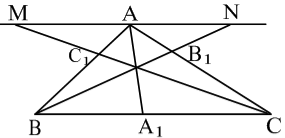 Проведемо через вершину
Проведемо через вершину ![]() пряму, паралельну стороні
пряму, паралельну стороні ![]() (рис.17). Нехай пряма
(рис.17). Нехай пряма ![]() , перетинає цю пряму в точці
, перетинає цю пряму в точці ![]() , пряма
, пряма ![]() - в точці
- в точці ![]() .
.
![]() ~
~![]() , тому: Рис. 17
, тому: Рис. 17
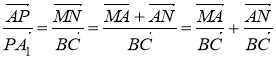 . (2)
. (2)
![]() ~
~![]() :
:
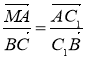 . (3)
. (3)
![]() ~
~![]() :
: 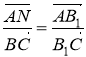 . (4)
. (4)
Підставивши рівності (3) і (4) у рівність (2), отримаємо (1), тобто
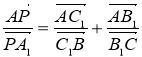 . Теорему доведено.[12]
. Теорему доведено.[12]
Теорема 6. (Теорема про метелика). Якщо через точку Р, що є серединою хорди EF деякого кола проведено дві довільні хорди АС і BD . Хорди АС і BD перетинають відрізок EF в точках X і Y . Довести, що точка P є серединою відрізка EF.
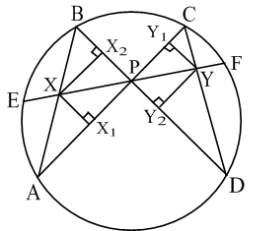 Доведення. Опустимо перпендикуляри із точок X і Y на прямі АС і BD (рис. 18). Оскільки
Доведення. Опустимо перпендикуляри із точок X і Y на прямі АС і BD (рис. 18). Оскільки ![]() (так як
(так як ![]() , як вписані, що спираються на одну й ту саму дугу), то
, як вписані, що спираються на одну й ту саму дугу), то 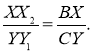 Оскільки
Оскільки ![]() (тому, що
(тому, що ![]() , як вертикальні), то
, як вертикальні), то 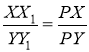 . Так само з
. Так само з ![]() (
(![]() , як вертикальні) маємо:
, як вертикальні) маємо: 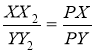 . Рис. 18
. Рис. 18
Оскільки ![]() , то
, то 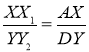 .
.
Введемо позначення: ![]() , далі матимемо:
, далі матимемо:
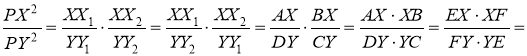
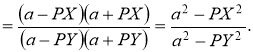
А це означає, ![]()
Тобто ![]() . Розкривши дужки і звівши подібні доданки, отримаємо
. Розкривши дужки і звівши подібні доданки, отримаємо ![]() , тобто
, тобто ![]() , що й потрібно було довести.
, що й потрібно було довести.
Теорема 7. Формула Герона визначає площу трикутника ![]() за довжиною його сторін
за довжиною його сторін ![]() .
.
![]() , де
, де ![]() .
.
Доведення. На рис. 19 зображено зовні вписане коло ![]() трикутника
трикутника ![]() ,
, ![]() - центр цього кола,
- центр цього кола, ![]() - інцентр трикутника
- інцентр трикутника ![]() ,
, ![]() - точки дотику вписаного і зовні вписаного кіл трикутника
- точки дотику вписаного і зовні вписаного кіл трикутника ![]() до
до ![]() .
.
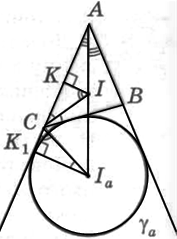
![]() . Тоді
. Тоді ![]() ~
~![]() .
.
З подібності трикутників випливає: 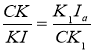 , тобто
, тобто 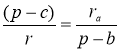 і
і ![]() .
.
Запишемо такі три рівності: ![]() ,
, ![]() ,
,![]() . Перемножимо перші дві з них і врахуємо третю: Рис. 19
. Перемножимо перші дві з них і врахуємо третю: Рис. 19
![]() , маємо формулу Герона
, маємо формулу Герона ![]() .[1]
.[1]
Теорема 8. Якщо ![]() - бісектриса
- бісектриса ![]() (рис.20), тоді
(рис.20), тоді ![]() ( в позначеннях рис.21
( в позначеннях рис.21![]() ).
).
Доведення. Опишемо навколо трикутника ![]() коло, точку перетину прямої
коло, точку перетину прямої ![]() і кола позначимо К (рис. 21).
і кола позначимо К (рис. 21).
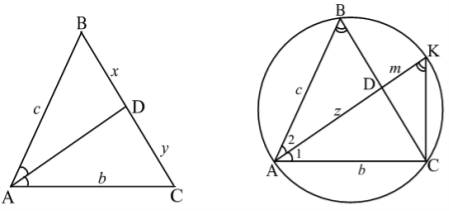
Рис. 20 Рис. 21
Позначимо ![]() .
. ![]() (оскільки
(оскільки ![]() і
і ![]() . З подібності випливає
. З подібності випливає ![]() , тобто
, тобто ![]() , звідки
, звідки ![]() . За властивістю перетинаючих хорд
. За властивістю перетинаючих хорд ![]() , тобто
, тобто ![]() , тоді
, тоді ![]() ,
, ![]() . Теорему доведено.
. Теорему доведено.
3. Властивості трапеції, які доводяться за допомогою подібності трикутників
Теорема 9. В довільній трапеції точки перетину продовження бічних
сторін та середини її основ лежать на одній прямій.
Доведення. Розглянемо трапецію ![]() . Нехай точка
. Нехай точка ![]() - середина
- середина
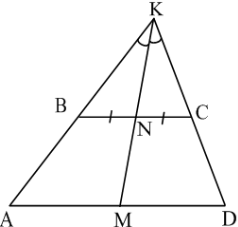 основи
основи ![]() ,
, ![]() - точка перетину продовження бічних сторін (рис. 22). Так як
- точка перетину продовження бічних сторін (рис. 22). Так як ![]() і
і ![]() , то
, то ![]() ~
~![]() і
і ![]() ~
~![]() . Звідси
. Звідси ![]()
Оскільки ![]() (за умовою), то з останньої рівності випливає, що
(за умовою), то з останньої рівності випливає, що ![]() А це означає, що точки
А це означає, що точки ![]() лежать
лежать
на одній прямій. Теорему доведено.[1] Рис. 22
Теорема 10. В довільній трапеції точки перетину діагоналей та середини її основ лежать на одній прямій.
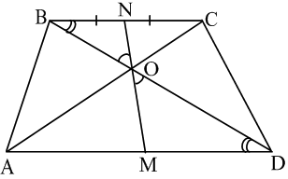 Доведення. Розглянемо трапецію
Доведення. Розглянемо трапецію ![]() Нехай точка
Нехай точка ![]() - середина основи
- середина основи ![]() ,
, ![]() - точка перетину діагоналей (рис. 23 ).
- точка перетину діагоналей (рис. 23 ).
Так як ![]() ,
, ![]() - січна, то
- січна, то ![]() , а
, а ![]() (як вертикальні). Звідси
(як вертикальні). Звідси ![]() . Рис. 23
. Рис. 23
Аналогічно і ![]() ~
~![]() . З подібності трикутників маємо:
. З подібності трикутників маємо: ![]() .
.
Оскільки ![]() (за умовою), то з останньої рівності випливає, що
(за умовою), то з останньої рівності випливає, що ![]() . А це означає, що точки
. А це означає, що точки ![]() лежать на одній прямій. Теорему доведено [1].
лежать на одній прямій. Теорему доведено [1].
Теорема 11. (Теорема про чотири точки трапеції). В довільній трапеції середини основ, точка перетину діагоналей, точка перетину продовження бічних сторін лежать на одній прямій.
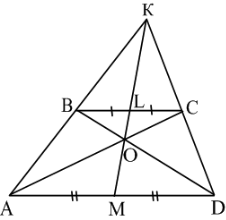 Доведення. Розглянемо трапецію
Доведення. Розглянемо трапецію ![]() . Нехай точки
. Нехай точки ![]() і
і ![]() – середини основ
– середини основ ![]() і
і ![]() відповідно,
відповідно, ![]() - точка перетину діагоналей,
- точка перетину діагоналей, ![]() - точка перетину продовження бічних сторін (рис. 24). Так як
- точка перетину продовження бічних сторін (рис. 24). Так як ![]() лежать на одній прямій – за теоремою 1.9 і
лежать на одній прямій – за теоремою 1.9 і ![]() лежать на одній прямій - теоремою 1.10. Тоді
лежать на одній прямій - теоремою 1.10. Тоді ![]() , тобто лежать на одній прямій. Теорему доведено. Рис. 24
, тобто лежать на одній прямій. Теорему доведено. Рис. 24
Теорема 12. Відрізок, паралельний основам трапеції, кінці якого лежать на бічних сторонах ціє трапеції, ділить одну з них у відношенні ![]() ( якщо рахувати від меншої основи) і дорівнює
( якщо рахувати від меншої основи) і дорівнює ![]() .
.
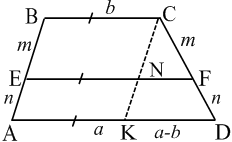 Доведення. Нехай
Доведення. Нехай ![]() , а
, а ![]() (рис. 25). Оскільки
(рис. 25). Оскільки ![]() за побудовою і
за побудовою і ![]() , то маємо:
, то маємо: ![]() ,
, ![]() .
.
Так як ![]() , тоді
, тоді ![]() ~
~![]() , звідси Рис. 25
, звідси Рис. 25
![]() і
і ![]()
Отже, ![]() .
.
Теорему доведено.[4]
Теорема 13. Відрізок, паралельний основам трапеції, кінці якого належать бічним сторонам трапеції, проходить через точку перетину діагоналей цієї трапеції і цією точкою ділиться навпіл.
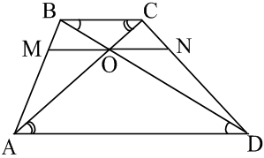 Доведення. Нехай
Доведення. Нехай ![]() - точка перетину діагоналей,
- точка перетину діагоналей, ![]() , доведемо, що
, доведемо, що ![]() (рис. 26). Оскільки
(рис. 26). Оскільки ![]() , тоді
, тоді ![]() ~
~![]() , звідси
, звідси ![]() . Аналогічно
. Аналогічно ![]() ~
~![]() , звідси
, звідси ![]() . За узагальненою теоремою Фалеса
. За узагальненою теоремою Фалеса ![]() , тоді
, тоді ![]() і
і ![]() , що і потрібно було довести. Рис. 26
, що і потрібно було довести. Рис. 26
Теорема 14. Відрізок, паралельний основам трапеції, кінці якого належать бічним сторонам трапеції, проходить через точку перетину діагоналей цієї трапеції ділить бічну сторону і кожну діагональ трапеції на відрізки, пропорційні прилеглим сторонам.
Доведення. За умовою задачі маємо ![]() ,
,![]() (рис.26). Доведемо
(рис.26). Доведемо ![]() (1) і
(1) і ![]() (2). Оскільки
(2). Оскільки ![]()
![]() - січна, то
- січна, то ![]() і
і ![]() . Тоді
. Тоді ![]() ~
~![]() , звідси
, звідси ![]() , (1) –доведено. Оскільки
, (1) –доведено. Оскільки ![]() , тоді за узагальненою теоремою Фалеса:
, тоді за узагальненою теоремою Фалеса:
![]() (2) – доведено. Теорему доведено.[1]
(2) – доведено. Теорему доведено.[1]
Теорема 15. Відрізок, що проходить через точку перетину діагоналей трапеції паралельний її основам, перетинає бічні сторони трапеції в точках М і N має довжину, що дорівнює відношенню подвоєного добутку довжин основ трапеції до суми цих сторін, тобто
![]() .
.
Доведення. Нехай ![]() – точка перетину діагоналей,
– точка перетину діагоналей, ![]() ,
, ![]() (рис. 26), очевидно, що
(рис. 26), очевидно, що ![]() , тому
, тому![]() ~
~![]() , звідси:
, звідси:
![]() . (1)
. (1)
Основи трапеції паралельні, тому, ![]() , і
, і ![]() , тоді за першою ознакою подібності
, тоді за першою ознакою подібності ![]() ~
~![]() , звідси
, звідси ![]() , тобто
, тобто![]() .
.
Враховуючи, що ![]() знаходимо відношення
знаходимо відношення ![]() Підставляючи це у рівняння (1), отримуємо,
Підставляючи це у рівняння (1), отримуємо, ![]() Аналогічно знаходимо, що
Аналогічно знаходимо, що ![]()
![]() таким чином
таким чином ![]() . Теорему доведено.[1]
. Теорему доведено.[1]
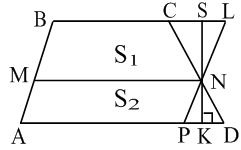 Теорема 16. В довільній трапеції, відрізок паралельний основам трапеції розбиває її на дві рівновеликі трапеції і дорівнює
Теорема 16. В довільній трапеції, відрізок паралельний основам трапеції розбиває її на дві рівновеликі трапеції і дорівнює 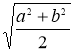 .
.
Доведення. Розглянемо трапецію ![]() ,
, ![]() , відрізок
, відрізок ![]() розбиває її на дві рівновеликі трапеції
розбиває її на дві рівновеликі трапеції ![]() і
і ![]() , тобто
, тобто ![]() Рис. 27
Рис. 27
(за умовою) (рис.27). Тоді ![]() , звідси
, звідси ![]() . Оскільки
. Оскільки ![]() , то
, то ![]() ~
~![]() , звідси маємо:
, звідси маємо: ![]() .
.
Отже, ![]() , тоді
, тоді 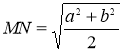 , що і потрібно було довести .[4]
, що і потрібно було довести .[4]
Теорема 17. У трапеції відрізок, що сполучає середину однієї основи з кінцем другої основи, перетинає діагональ у точці ![]() і на прямій, проведеній через точку
і на прямій, проведеній через точку ![]() паралельно основам, діагоналі відсікають рівні відрізки.
паралельно основам, діагоналі відсікають рівні відрізки.
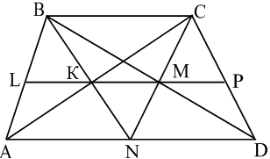 Доведення. Нехай маємо трапецію
Доведення. Нехай маємо трапецію ![]() ,
, ![]() - середина нижньої основи
- середина нижньої основи ![]() і відрізок
і відрізок ![]() перетинає діагональ
перетинає діагональ ![]() у точці
у точці ![]() . Пряма
. Пряма ![]() , що
, що
проходить через точку ![]() паралельно основам, перетинає другу діагональ у точці
паралельно основам, перетинає другу діагональ у точці ![]() , а бічні сторони
, а бічні сторони ![]() і
і ![]() - у точках
- у точках ![]() і
і ![]() відповідно. Доведемо, що
відповідно. Доведемо, що ![]() (рис. 28). Рис. 28
(рис. 28). Рис. 28
Рівність відрізків ![]() і
і ![]() випливає з того, що трикутники
випливає з того, що трикутники ![]() і
і ![]() гомотетичні з центром гомотетії в точці
гомотетичні з центром гомотетії в точці ![]() .
.
Оскільки ![]() , то і
, то і ![]() . Аналогічно, якщо провести відрізок
. Аналогічно, якщо провести відрізок ![]() , то він перетне діагональ
, то він перетне діагональ ![]() в точці
в точці ![]() такій, що
такій, що ![]() бо трикутники
бо трикутники ![]() і
і ![]() гомотетичні і
гомотетичні і ![]() . Отже,
. Отже, ![]() . Теорему доведено.[4]
. Теорему доведено.[4]
4. Задачі прикладного змісту при вивченні подібності трикутників в основній школі
Державний стандарт базової і повної загальної середньої освіти ґрунтується на засадах особистісно орієнтованого, компетентнісного і діяльнісного підходів. Діяльнісний підхід спрямований на розвиток умінь і навичок учня, застосування знань у практичних ситуаціях, пошук шляхів інтеграції до соціокультурного та природного середовища. Прикладні задачі, зокрема, з геометрії є засобом формування вмінь і навичок учня, застосовувати знання у практичних ситуаціях.
У навчанні математики розрізняють поняття «прикладна» і «практична» спрямованість. Прикладна спрямованість сприяє формуванню наукового світогляду і показує роль математики в сучасному виробництві, економіці, науці. Практична спрямованість навчання математики – “це спрямованість змісту і методів навчання на розв’язування задач і вправ, на формування у школярів навичок самостійної діяльності математичного характеру”.[6] Слід відзначити, що прикладне спрямування включає вміння учнів засобами математики досліджувати реальні явища, складати математичні моделі задач та співставляти отримані результати з реальними. А практичне спрямування шкільного курсу математики передбачає формування в учнів умінь використовувати здобуті знання під час вивчення як самої математики, так і інших дисциплін.
У школі під прикладними задачами розуміють задачі, які виникли поза математикою, але розв’язуються математичними засобами. СоколенкоЛ.О., Філон Л.Г. та Швець В.О. вважають, що прикладна задача має задовольняти такі методичні вимоги: 1) задачі повинні мати реальний практичний зміст, який забезпечує ілюстрацію практичної цінності і значущості набутих математичних знань; 2) задачі повинні відповідати шкільним програмах і чинним підручникам щодо методів і фактів, які будуть використовуватися в процесі їх розв’язування; 3) прикладні задачі повинні демонструвати практичне застосування математичних ідей у різних галузях; 4) зміст задачі повинен викликати в учнів пізнавальний інтерес, давати можливість демонструвати ефективне використання математичних знань на практиці.11
Розв'язування прикладних задач на уроках геометрії сприяє підвищенню ефективності навчання математики. При вивченні теми «Подібність трикутників» учні вчаться застосовувати ознаки подібності трикутників при розв’язуванні практичних задач. Після засвоєння ознак подібності трикутників, доречно показати застосування вивчених знань на практиці. Оскільки, процесу розв’язування прикладних задач властиві всі етапи математичного моделювання, то етапи розв’язання геометричних задач прикладного змісту з теми «Подібність трикутників» наступні:
-
 Створення математичної моделі. Демонстрація умови задачі за допомогою наочності, технічних засобів.
Створення математичної моделі. Демонстрація умови задачі за допомогою наочності, технічних засобів.
- Дослідження математичної задачі. Розв’язання задачі за допомогою математичних знань, зокрема, ознак подібності трикутників.
- Інтерпретація розв’язків. Переклад отриманих результатів з математичної на загальновживану мову
У шкільних підручниках у переважній більшості запропоновані задачі на знаходження недоступної відстані. Ці задачі можна розв’язувати різними способами, адже виміряти недоступну відстань можна за допомогою: власної тіні, кілочка з планкою, дзеркального відображення тощо. Наприклад: знайти висоту дерева Рис. 29
можна за допомогою власної тіні в сонячну погоду або за допомогою кілочка з планкою – в похмуру. Відомий математик Фалес Мілетський саме таким способом виміряв висоту піраміди за довжиною власної тіні.
У шкільних підручниках до задач цього можна віднести такі:
- Знайдіть висоту дерева, якщо довжина його тіні дорівнює 8,4 м, а тінь від вертикального стовпа заввишки 2 м у той самий час дорівнює 2,4 м.[1]
- Тінь від башти дорівнює 24 м, а вертикальний шест довжиною 1,2 м в ту саму пору дня має тінь завдовжки 80 см. Яка висота башти?[2]
- Довжина тіні фабричної труби дорівнює 35,8 м. У той самий час вертикально поставлена жердина завдовжки 1,9 м дає тінь довжиною 1,62 м. Знайдіть висоту труби.[4]
- Довжина тіні від вишки 14м, а від вертикальної двометрової палиці 1м. Знайдіть висоту вишки.[3]
- Довжина тіні дерева дорівнює 10,2 м, а довжина тіні людини, зріст якої 1,7 м,дорівнює 2,5 м. Знайдіть висоту дерева. [6]
- Зображення дерева, віддаленого на 60 м від об’єктива фотоапарата, має на плівці висоту 8 мм. Відстань віл об’єктива до зображення дорівнює 40мм. Яка висота дерева?
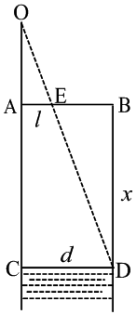
У шкільних підручниках є готові рисунки до таких задач і це значно полегшує розв’язування задачі. Так можна показати як виміряти глибину колодязя ![]() використовуючи подібність трикутників за допомогою вимірювального шеста даної висоти
використовуючи подібність трикутників за допомогою вимірювального шеста даної висоти ![]() (рис. 29). Для цього спочатку виміряємо довжину проекції «межі води і стіни» - точки
(рис. 29). Для цього спочатку виміряємо довжину проекції «межі води і стіни» - точки ![]() на діаметр колодязя
на діаметр колодязя ![]() , коли спостерігач дивиться з точки
, коли спостерігач дивиться з точки ![]() , тобто відрізок
, тобто відрізок ![]() . Прямокутні трикутники
. Прямокутні трикутники ![]() і
і ![]() подібні.
подібні.
Тоді ![]() . Звідси шукана
. Звідси шукана
глибина колодязя ![]() .
.
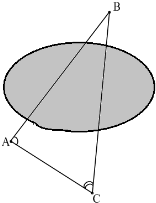 При розв’язуванні задач на знаходження відстані до недоступної точки, як правило використовують допоміжний рисунок на якому зображається подібний трикутник до даного (якщо задача прикладного змісту рекомендується обирати масштаб 1:1000). Наприклад, якщо нам потрібно знайти відстань від пункту
При розв’язуванні задач на знаходження відстані до недоступної точки, як правило використовують допоміжний рисунок на якому зображається подібний трикутник до даного (якщо задача прикладного змісту рекомендується обирати масштаб 1:1000). Наприклад, якщо нам потрібно знайти відстань від пункту ![]() до недосяжного пункту
до недосяжного пункту ![]() (рис. 30) то спершу виберемо точку
(рис. 30) то спершу виберемо точку ![]() так, щоб можна було провести відрізок
так, щоб можна було провести відрізок ![]() . Вимірявши кути
. Вимірявши кути ![]() і
і ![]() на Рис. 30
на Рис. 30
місцевості ми можемо побудувати подібний трикутник до даного на аркуші паперу (за відомими кутами). Отримаємо два подібних трикутники. Вимірявши довжини сторін у нашому допоміжному трикутнику, і за співвідношенням відповідних сторін знайдемо шукану відстань, тобто відстань до недоступної точки. Задачі цього типу є дещо важчими, та їх набагато менша кількість пропонується в шкільних підручниках, на відміну від попередніх. Наприклад:
-
У трикутнику
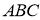 усі вершини недоступні. Як визначити довжини усіх його сторін? [5]
усі вершини недоступні. Як визначити довжини усіх його сторін? [5]
-
Як знайти відстань між двома пунктами
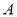 і
і 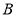 , між якими не можна пройти? [5]
, між якими не можна пройти? [5]
Розв’язування задач прикладного змісту на уроках геометрії сприятиме підвищенню ефективності навчання математики, розвитку уяви, логічного мислення учнів. Застосовування сучасних комп’ютерних технологій забезпечуватиме яскраву, динамічну наочну ілюстрацію умови задачі, спонукатиме учнів до вивчення геометрії завдяки цікавим прикладним задачам. Доцільно залучати учнів до самостійного пошуку
геометричних прикладних задач у практичній діяльності людини.
5. Методика розв’язування задач на побудову методом подібності в шкільному курсі математики
Вивчення геометрії у загальноосвітній школі сприяє всебічному розвитку школярів, зокрема, розвитку логічного мислення, просторової уяви, математичної ініціативи. Вивчення подібності, як правило, для учнів є дещо важчим і складнішим, на відміну від інших тем. Подібність розглядається у шкільному курсі геометрії двічі – у 8 класі при вивченні теми «Подібність трикутників» та у 9 при вивченні теми «Геометричні перетворення». Спочатку учні ознайомлюються з подібними фігурами, а потім вже вивчають перетворення подібності. Оскільки тема «Геометричні перетворення» вивчається після засвоєння учнями основних планіметричних фігур і їх властивостей, то вважаємо за доцільне ознайомити учнів з методом подібності як ще з одним методом розв’язування геометричних задач на побудову. Суть цього методу полягає у побудові допоміжної фігури, яка подібна шуканій і задовольняє умову частково, тобто визначає її форму. А потім будується вже кінцева фігура, за даними розмірами і яка повністю задовольняє всі умови задачі. При розв’язанні таких задач, як правило використовується гомотетія.
Шкільні задачі на побудову, що розв’язуються методом подібності поділяють на три типи за способом задання розмірів шуканої фігури: задачі, в яких розміри шуканої фігури визначаються заданням деякого відрізка; задачі, в яких розміри шуканої фігури визначаються заданням суми, різниці або частки деяких її відрізків; задачі, в яких розміри шуканої фігури визначаються положенням її відносно даних фігур.[4]
Розв’язування задач першого типу так як і всіх інших розпочинається з аналізу. Перш ніж приступити до розв’язування даної задачі на побудову доцільно сформувати певні умови, які повинна задовольняти шукана фігура за умовою задачі, а далі вже приступати до наступних етапів.
Як правило, задачі І типу є одними з найлегших задач на побудову, що розв’язуються методом подібності. Наприклад, побудувати трикутник за двома кутами та висотою (медіаною, бісектрисою). Спочатку ми будуємо довільний трикутник за двома кутами, тобто допоміжну фігуру, яка частково задовольняє умову задачі. Потім проводимо висоту (медіану, бісектрису) в цьому трикутнику, і на її продовженні відкладемо даний відрізок, що є висотою (медіаною, бісектрисою) шуканого трикутника. Далі будуємо пряму паралельну до основи допоміжного трикутника через точку, яка є кінцем даної висоти (медіани, бісектриси).
У шкільних підручниках геометрії пропонуються такі задачі І типу:
- Побудуйте трикутник за двома кутами і медіаною (бісектрисою і висотою), проведеною з вершини третього кута.[2]
- Побудуйте трикутник за двома кутами і найбільшою висотою.[5]
- Побудуйте трикутник за двома кутами і найменшою медіаною.[5]
-
Побудуйте трикутник, кути якого дорівнюють
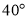 і
і 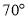 , а висота, проведена з вершини третього кута, дорівнює 5 см. Сам бевз
, а висота, проведена з вершини третього кута, дорівнює 5 см. Сам бевз
- Побудуйте трикутник за двома його кутами і радіусом вписаного чи описаного кола.[2]
- Побудувати трикутник за стороною, протилежним їй кутом і висотою, проведеною з вершини цього кута.[5]
Розв’язування задач ІІ типу, як правило, складніші і розв’язання більш громіздкі. Спочатку також будується допоміжна фігура, яка частково задовольняє умову задачі. Потім виходячи з суми, різниці, частки елементів фігури, що задано, відкладаються відрізки тих сторін, що потрібно, в допоміжній фігурі. Наприклад, якщо потрібно побудувати трикутник за кутом і периметром, то побудувавши допоміжний трикутник – довільний трикутник із даним кутом, на продовженні однієї із сторін кута відкладаємо ще дві його сторони, потім відкладемо на цій же прямій від вершини довжину периметра, що задано в умові. Далі застосовується гомотетія з центром в точці, яка є одним із кінців побудованої суми, різниці, частки певних відрізків. Побудувавши відповідні сторони отримаємо шукану фігуру.
У шкільних підручниках геометрії пропонуються такі задачі ІІ типу:
- Побудуйте трикутник даного периметра, подібний даному трикутнику.[2]
- Побудуйте паралелограм даного периметра, подібний даному паралелограму. [2]
- Побудуйте трикутник за відношенням сторін та: 1) найбільшою медіаною; 2) найменшою висотою.[5]
- Побудувати рівнобедрений трикутник за: а) кутом при вершині та сумою основи з висотою; б) відношенням двох нерівних сторін та висотою, проведеною до бічної сторони.[5]
- Побудуйте прямокутний трикутник за найменшою висотою і відношення проекцій катетів на гіпотенузу.[5]
- Побудуйте трикутник за відношенням двох сторін, кутом між ними і бісектрисою цього кута.[5]
- Побудувати трикутник за двома кутами та периметром.[5]
-
Побудуйте трикутник
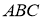 за даною медіаною
за даною медіаною 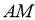 і відношенням
і відношенням 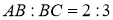 , якщо
, якщо 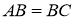 .
.
- Побудуйте прямокутний трикутник за гіпотенузою і відношенням катетів.[5]
Задачі ІІІ типу є найскладнішими для учнів, адже перед ними стоїть завдання, яке визначає положення шуканої фігури відносно даної. Перш ніж приступити до розв’язування задач такого типу потрібно добре подумати, пригадати деякі властивості фігур, які потрібно побудувати (наприклад: квадрат, ромб, прямокутник). Задачі цього типу вимагають ґрунтовного аналізу. Побудова проводиться аналогічно до попередніх задач: спочатку будується допоміжна фігура, яка визначає форму шуканої фігури і задовольняє умову задачі частково; далі розглядається гомотетія з центом в точці відносно даної фігури і будується шукана фігура.
У шкільних підручниках геометрії пропонуються такі задачі ІІІ типу:
- У даний ромб впишіть квадрат так, щоб на кожній стороні ромба була одна вершина квадрата.[1]
-
У гострокутний трикутник
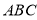 впишіть квадрат так, щоб дві його вершини лежали відповідно на сторонах
впишіть квадрат так, щоб дві його вершини лежали відповідно на сторонах 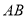 і
і 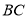 , а дві інші – на стороні
, а дві інші – на стороні  .[9]
.[9]
- Через точку внутрішньої області даного кута проведіть коло, яке дотикається до його сторін.[5].
-
Впишіть у трикутник
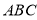 такий трикутник, сторони якого відповідно перпендикулярні до сторін трикутника
такий трикутник, сторони якого відповідно перпендикулярні до сторін трикутника 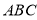 .[5]
.[5]
- У дане коло впишіть трикутник:
а) подібний даному;
б) сторони якого паралельні сторонам даного трикутника.[5]
-
Впишіть у трикутник
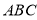 прямокутник, у якого основа втричі більша за висоту і лежить на основі трикутника, а дві вершини лежать на його бічних сторонах.[5]
прямокутник, у якого основа втричі більша за висоту і лежить на основі трикутника, а дві вершини лежать на його бічних сторонах.[5]
- У даний трикутник впишіть прямокутник, сторони якого пропорційні числам 2 і 3 так, щоб одна його сторона лежала на основі трикутника, а дві інші - на бічних сторонах.[2]
- У даний трикутник впишіть ромб так, щоб один кут у них був спільний, а протилежна вершина ромба лежала на стороні, протилежній до цього кута.[2]
Побудовані фігури ще не є кінцевими розв’язками задач. Потрібно ще довести той факт, що дана фігура є шуканою і провести дослідження скільки розв’язків має задача при довільному виборі її елементів.
Як правило при доведенні того факту, що побудована фігура є шуканою використовують знання про подібні фігури – це можуть бути ознаки подібності трикутників, з яких випливає пропорційність сторін і рівність кутів. Доведення в більшості випадків випливає з побудови, і найчастіше використовується подібність.
Для розв’язання задач на побудову методом подібності можна сформувати такий алгоритм:
- Зробити ґрунтовний аналіз, сформувавши певні умови, які повинна задовольняти шукана фігура за умовою задачі.
- Побудувати допоміжну фігуру, яка частково задовольняє умову, тобто визначає форму шуканої фігури;
- Використовуючи дані відрізки чи положення шуканої фігури відносно даної - зробити певні побудови, в залежності від задачі.
- Використовуючи гомотетію знайти точки, що будуть вершинами нашої фігури.
- Побудувати шукану фігуру.
- Провести доведення, яке як правило випливає з побудови.
- Дослідження.
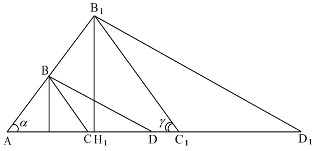
Розглянемо приклад: побудувати трикутник за двома кутами при основі ![]() і
і ![]() та сумою висоти з основою
та сумою висоти з основою ![]() , проведеною з вершини третього кута.
, проведеною з вершини третього кута.
Розв’язання
І. Аналіз. Шуканий трикутник повинен задовольняти двом умовам:
1) кути при основі повинні дорівнювати ![]() і
і ![]() ; 2) сума висоти з основою повинна дорівнювати даному відрізку
; 2) сума висоти з основою повинна дорівнювати даному відрізку ![]() .
.
 Нехай ми побудували
Нехай ми побудували ![]() (рис. 31), який задовольняє першу умову, тобто
(рис. 31), який задовольняє першу умову, тобто ![]() ,
, ![]() . Шуканий трикутник будемо шукати серед трикутників подібних до
. Шуканий трикутник будемо шукати серед трикутників подібних до ![]() , відносно будь-якого центра подібності, наприклад т.
, відносно будь-якого центра подібності, наприклад т.![]() . Нехай
. Нехай ![]() - шуканий. Зрозуміло, що
- шуканий. Зрозуміло, що ![]()
![]()
![]() . Якщо при деякому перетворенні подібності точці
. Якщо при деякому перетворенні подібності точці ![]() Рис.31
Рис.31
відповідає точка ![]() , то точці
, то точці ![]() відповідає
відповідає ![]() . Знайдемо коефіцієнт подібності, що переводить
. Знайдемо коефіцієнт подібності, що переводить ![]() у
у ![]() . За умовою даний відрізок
. За умовою даний відрізок ![]() , а за побудованим
, а за побудованим![]() ми можемо побудувати
ми можемо побудувати ![]() . Тоді шуканий коефіцієнт подібності дорівнює
. Тоді шуканий коефіцієнт подібності дорівнює ![]() . Отже,
. Отже, ![]() ~
~![]() відносно центра подібності
відносно центра подібності ![]() . За цими даними
. За цими даними ![]() може бути побудований.
може бути побудований.
ІІ. Побудова.
-
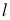 ,
, 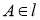 ,
, 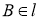 ;
;
-
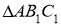 , (
, (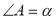 ,
,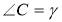 )
)
-
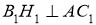 ;
;
-
Відкладемо на продовженні
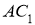 ,
, 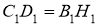 , тобто
, тобто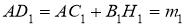 ;
;
-
Відкладемо на продовженні
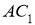 ,
, 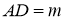 .
.
-
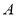 - центр гомотетії,
- центр гомотетії, 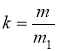 .
. 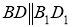 ,
, 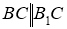 ;
;
-
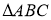 - шуканий.
- шуканий.
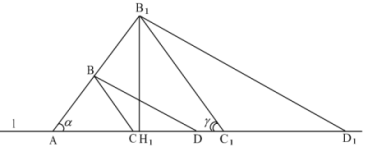
Рис. 32
ІІІ. Доведення. ![]() ~
~![]() (за 2 кутами).
(за 2 кутами).
ІV. Дослідження. Трикутник не існує, якщо ![]()
![]()
![]() . Розв’язок задачі єдиний.
. Розв’язок задачі єдиний.
На сьогодні є актуальним використання мультимедійних технологій у навчанні геометрії. Зокрема при розв’язуванні задач методом подібності на побудову можна скористатися програмою GeoGebra. За допомогою цієї програми можна виконувати точні побудови, демонструвати різні перетворення та ін. На рис. 34. виконано побудову до задачі: дано кут і всередині нього точку ![]() . Побудувати коло, яке дотикається до сторін кута і проходить через точку
. Побудувати коло, яке дотикається до сторін кута і проходить через точку ![]() .
.
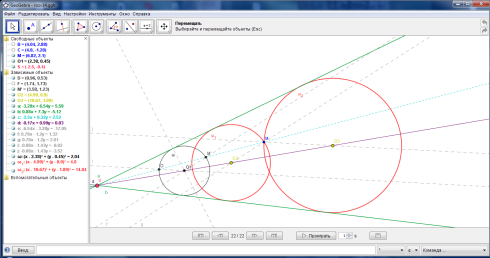
Рис. 33
Крім того, використання новітніх технологій значно економить час на уроці, що є дуже важливим аспектом у навчанні дітей. А учням, в свою чергу, дуже подобаються такі уроки, адже їм цікаво і хочеться працювати.
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
- Апостолова Г.В. Геометрія. 8 клас. Підручник для учнів 8 класу / Г.В.Апостолова. – К.: «Генеза». – 2008. – С.116-117.
- Бевз Г.П. Геометрія. 8 клас. Підручник для учнів 8 класу / Г.П. Бевз, В.Г.Бевз, Н.Г. Владімірова. – К.: «Вежа». – 2008. – С.80-81.
- Бевз Г.П. Методика викладання математики/ Г.П. Бевз. – К.: Вища школа, 1989. – С.327.
- Боровик В.Н. Геометричні перетворення площини. Навчальний посібник / В. Н. Боровик, І. В. Зайченко, М.М. Мурач, В.П. Яковець. – Суми: «Університетська книга». – 2003. – С. 249-260.
- Бурда М.І. Геометрія. 8 клас. Підручник для учнів 8 класу / М.І. Бурда, Н.А. Тарасенкова – К.: «Зодіак-Еко». – 2008. – С.80-81.
- Грицик Т. Прикладні задачі під час вивчення лінійних та квадратних рівнянь / Т. Грицик, В. Забранський // Математика в школі. – 2010. - №12. – С.14-19.
- Гришина Т.О. Повне опрацювання понять на уроці геометрії. / Т.О.Гришина // Математика в школі. – 1999. - №3. – С.23-26.
- Єршова А.П. Геометрія. 8 клас. Підручник для учнів 8 класу / А.П.Єршова, В.В. Голобородько, О.Ф. Крижановський, С.В.Єршов. – К.: «Ранок». – 2008. – С.105.
- Мерзляк А.Г. Геометрія. 8 клас. Підручник для учнів 8 класу / А.Г.Мерзляк, В.Б. Полонський, М.С. Якір. – К.: «Гімназія». – 2008. – С.86-87.
- Слєпкань З. І. Методика навчання математики: Підручник. – 2-ге видання, допов. і переробл. – К.: Вища шк., 2006. – С.68.
- Соколенко Л.О. Прикладні задачі природничого характеру в курсі алгебри і початків аналізу: практикум. Навчальний посібник. / Л.О.Соколенко, Л.Г.Філон, В.О.Швець. – К.: НПУ імені М.П.Драгоманова. - 2010. С. 128.
- Ясінський В.А. Олімпіадні задачі з геометрії. Навч. – метод. посібник/ В.А.Ясінський. – К.: «Шкільний світ». – 2008. С. 11, 14-15.
1


про публікацію авторської розробки
Додати розробку
