Перпендикуляр та похила у просторі. Теорема про три перпендикуляри
Перпендикуляр та похила у просторі. Теорема про три перпендикуляри
Те, що ми знаємо, - обмежено, а те, що ми не знаємо, - нескінченно.
П'єр-Симон Лаплас
Мета: Формування та закріплення вмінь учнів розв’язувати задачі на використання ознаки та властивостей перпендикулярності прямої та площини, теореми про три перпендикуляри, властивості похилих. Поглиблення та розширення навчальних досягнень, усунення прогалин у знаннях, виявлення зацікавленості до вивченої теми програмного матеріалу. Контроль сформованості умінь самостійно застосовувати набуті знання при виконанні практичних завдань. Розвиток ініціативи і творчості учнів, взаємної зацікавленості у досягненні мети, розвиток математичного мовлення, графічної грамотності, охайності, самоствердження при доказах, вміння аналізувати, слухати товаришів. Виховання колективізму.
I Мотивація навчальної діяльності, повідомлення теми та мети уроку (формування мотивації навчально-пізнавальних дій, професійного становлення, потреби постійної самоосвіти)
Те, що ми знаємо, – обмежено, а те, що ми не знаємо – нескінченно. Навчання сьогодні - це те, що матиме наслідки у майбутньому, в якому ми живемо. За словами Пітера Друкера - економіста письменника, викладача університету, журналіста, адвоката, скульптора, бізнесмена та філософа: «Найкращий спосіб прогнозувати майбутнє - створити його».
Тому давайте спробуємо разом з’ясувати, як можна у повсякденному житті використати отримані на уроках геометрії теоретичні знання за темою «Перпендикуляр та похила, теорема про три перпендикуляри».
II Актуалізація чуттєвого досвіду та корекція опорних знань (усне опитування учнів: виявлення ступеня засвоєння вивченого на попередніх уроках теоретичного матеріалу)
- За даним малюнком назвати правило: (застосування учнями знань у стандартних умовах)
|
|
|
|
|
|
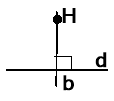
Малюнок 1 |
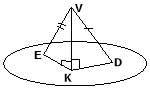
Малюнок 2 |
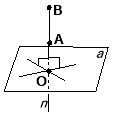
Малюнок 3 |
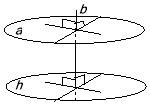
Малюнок 4 |
|
Перпендикуляр з точки до прямої або теорема про єдину перпендикулярну пряму з точки |
Властивість похилих |
Означення відрізка, перпендикулярного до площини |
Властивість перпендикулярності прямої та площини |
-
Продовжити правило:
- Відстанню між точками називається…(довжина відрізка);
- Дві прямі, перпендикулярні до однієї площини, між собою…(паралельні);
- Якщо пряма перпендикулярна до двох площин, то площини ….( паралельні);
- Перпендикуляр, це відрізок, розташований на (перпендикулярній прямій)… до площини та сполучає дану точку простору з ….(точкою площини);
- Відстанню від точки до прямої називається…(довжина перпендикуляра, опущеного з цієї точки на пряму);
- Якщо прямі перетинаються під кутом 900, вони…(перпендикулярні);
- Прямі мимобіжні, якщо вони…(не лежать в одній площині);
- У площині через точку на прямій можна провести…(тільки одну пряму, перпендикулярну даній прямій та безліч прямих, що її перетинають);
- У просторі через точку на прямій можна провести…( безліч прямих, перпендикулярних до даної прямої);
- На площині через точку, що не лежить на прямій можна провести…(тільки одну пряму, перпендикулярну до даної прямої та тільки їй паралельну).
- За допомогою власного досвіду спробуйте знайти відповіді на наступні запитання: (встановлення тісного зв'язку із життям, першою чергою — з особистим досвідом учня, творче перенесення учнями знань та вмінь у нові умови)
- Як на практиці за допомогою виска перевірити вертикальність встановленого стовпа? (Відповідь: Висок являє собою тягарець до якого прив’язаний шнурок. За законами всесвітнього тяжіння, якщо висок тримати за шнурок (висок у стані спокою), то висок є перпендикулярним до поверхні землі, а тому всі об’єкти які є паралельні до нього (у даному випадку стовп) є перпендикулярні до поверхні землі за рахунок чого вони є стійкими. Ця властивість використовується будівельниками при будівництві будинків, і інших споруд)
- Чому з точки по площиною на площину можна провести тільки один перпендикуляр? (Відповідь: перпендикуляр за означенням лежить на перпендикулярній прямій до площини, всі інші відрізки, що сполучають точку поза площиною з точками площини є похилими)
- Як слід встановити на хрестовині ялинку, щоб вона була перпендикулярна до площини підлоги? (Відповідь: за ознакою перпендикулярності прямої та площини, треба встановити ялинку так, щоб її стовбур був перпендикулярним до напрямів хрестовини)
- Чи має значення для знаходження кута між площиною і похилою, з якої точки похилої проведено перпендикуляр до площини? Чому? (Відповідь: ні тому, що сторони кута не впливають на розмір кута, а тільки градусна міра)
- Як перевірити за допомогою рулетки вертикальність стовпа? (Відповідь: Вибрати дві будь – які рівні проекції, що не розташовані на спільній прямій з основою стовпа та виміряти довжини похилих)
- Чому бурульки, які звисають з даху навесні, можна вважати паралельними між собою, нехтуючи їхньою товщиною? (Відповідь: Якщо дві прямі перпендикулярні до спільної площини, між собою вони паралельні)
- Наочною моделлю перпендикулярної прямої і площини є колесо зі спицями на вісь. Вісь перпендикулярна до кожної спиці. Під час руху колеса спиці описують площину круга, на якій містяться безліч відрізків, що перетинаються в одній точці. Якщо вісь розміщено горизонтально, то в якій площині буде обертатися колесо? Чому? (Відповідь: У площині, перпендикулярній до осі колеса, за ознакою перпендикулярності прямої та площини)
III Організація закріплення, систематизації знань учнів (застосовування отриманих знань при виконанні практичних завдань)
|
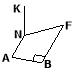
Задача № 1. Відрізок KN перпендикулярний до площини прямокутної трапеції NABF (ANBF). Провести з точки K перпендикуляри до прямих BF та АВ. Пояснити побудову. |
|
|
Розв’язання: NABF – прямокутна трапеція (ANBF), тому АВNA. Проведемо відрізки КА і КЕ та висоту трапеції NЕВF. Якщо KN(ABFN), тоді KAN, KEN – прямокутні. За ТТП, якщо проекції NAAB і NEBF, тоді і похилі АKAB і KEBF. |
|
|
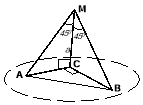
Задача № 2. З точки M проведено до площини похилі MA і MB та перпендикуляр MC. Довжина перпендикуляра MC=a. Кут між похилими та перпендикуляром 450. Знайти площі трикутників ABC і АМВ та кут між похилими, якщо проекції похилих перпендикулярні. (Відповідь: 600, |
|
|
Розв’язання: якщо МС перпендикуляр до площини, тоді МAС та МВС прямокутні зі спільним катетом МС та рівними кутами 450. МAС=МВС за другою ознакою рівності трикутників. Отримали АМС=ВМС=МАС=МВС=45°, МА=МВ, МС=АС=СВ=а. За теоремою Піфагора:
Якщо проекції похилих перпендикулярні, тоді AВС прямокутний,
|
|
|
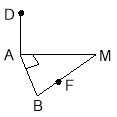
Задача № 3. Джерело світла (точка D) закріплено на деякій висоті від ділянки землі, що має форму прямокутного трикутника. Вказати точку F на бордюрі ділянки, який співпадає з гіпотенузою трикутника, де освітлення буде максимальним. Знайти відстань від землі до джерела освітлення, якщо довжина відрізка DF= 5м, і точка знаходження максимального освітлення F на бордюрі ділить гіпотенузу на відрізки довжиною 2 м та 8 м. (3 б.) (Відповідь: 3 м) |
|
|
(Розв’язання: За означенням відстані від точки до площини чи до прямої DA(АВM), DFBM. Невідомий відрізок - це довжина перпендикуляра DA. За теоремою про три перпендикуляри, якщо похила DFBM, тоді проекція AFBM. Проекція є висотою трикутника. Знаходимо її за правилом пропорційності висоти до гіпотенузи у прямокутному трикутнику. |
|
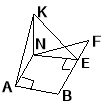
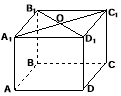
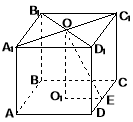
Задача № 4. Джерело світла (точка О) знаходиться в центрі стелі кімнати, що має форму прямокутного паралелепіпеда. Вказати точки на підлозі та на плінтусі підлоги (ребро DC), де освітлення буде максимальним. Знайти відстань від центра верхньої основи (точка О) паралелепіпеда до ребра DC, якщо AD= 8м, AA1=3 м. (3 б.) |
|
|
Розв’язання: Слід вказати дві точки О1 і Е, де освітлення буде максимальним. За означенням відстані від точки до площини чи прямої ОО1(АВС), ОЕDC. Невідомий відрізок, де максимальне освітлення – це відрізки ОО1 та ОЕ. За ТТП, якщо похила ОЕDC, тоді проекція О1ЕDC. Звідси довжина бічного ребра АА1=ОО1=3 м тому, що це довжина перпендикуляра до основи паралелепіпеда. Проекція О1Е дорівнює половині паралельної сторони, бо точка О1 –це проекція точки перетину діагоналей прямокутника. О1Е=0,5AD=4 м. За теоремою Піфагора довжина похилої ОЕ=5 м. |
|
IV Підсумок уроку (рефлексія)
- Як у побуті можна використати властивість похилих та їхніх проекцій? Приведіть приклади.
- Яке запитання та яка задача Вам найбільше подобалося? Обґрунтуйте вашу відповідь.
- Де ще з Вашої точки зору можна практично використовувати перпендикулярність прямих у просторі та перпендикулярність прямої та площини?
- Чи задоволені Ви уроком та своєю роботою?
1


про публікацію авторської розробки
Додати розробку