Презентація уроку "Скалярний добуток векторів. Кут між векторами"
Про матеріал
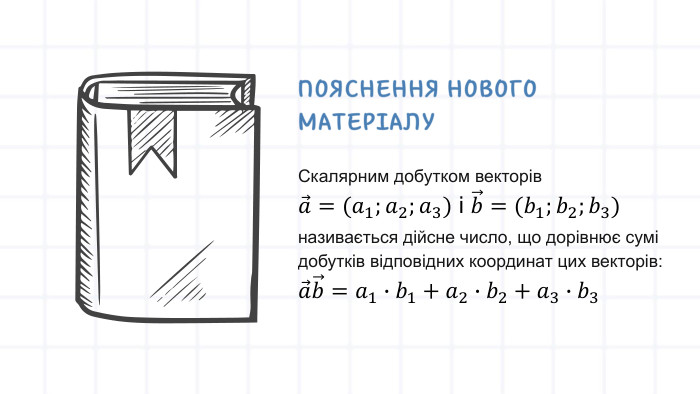
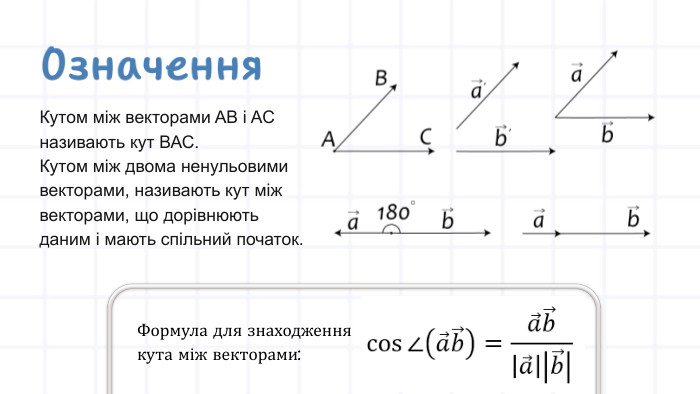
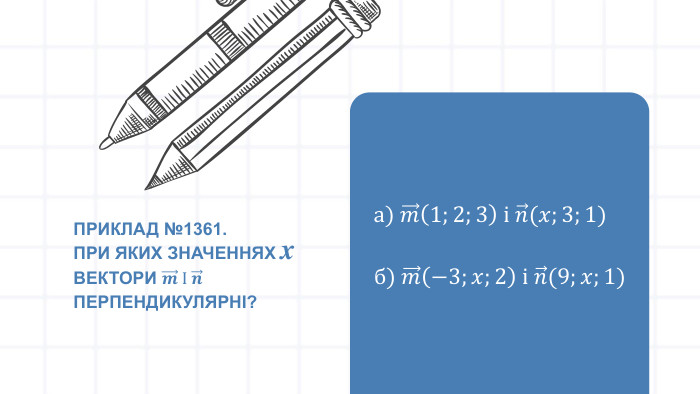
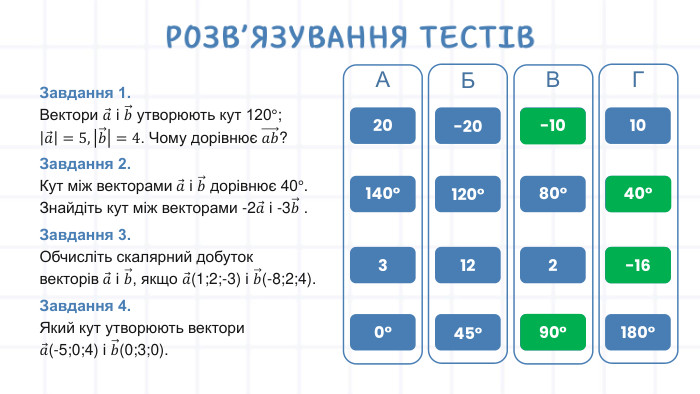
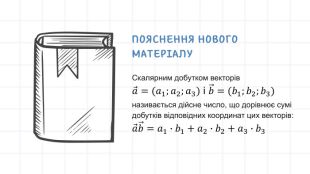
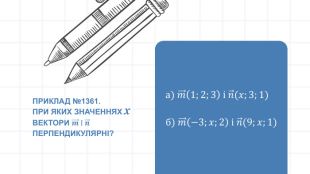
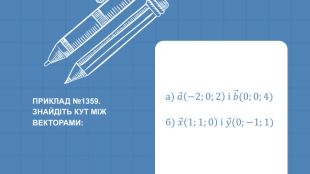
Урок "Скалярний добуток векторів. Кут між векторами" - це цікаве заняття, яке вивчає ключові математичні концепції. Учні детально вивчають скалярний добуток векторів та кут між ними. Презентація включає теорію, практичні завдання, тести та рефлексію. Учням пропонуються вправи та завдання для самостійного розв'язання, що допомагає закріпити матеріал. Тести служать для перевірки розуміння та рефлексії над отриманими знаннями. Урок розширює їхнє розуміння геометричних концепцій та надає практичні навички для використання їх у різних галузях. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку