"Перпендикулярність прямих і площин" Методичні розробки уроків геометрії для 10 класу з метою організації самостійної навчально- пізнавальної діяльності учнів та розвиток їх творчи

Про матеріал

Тематична папка використовується під час вивчення теми „ Перпендикулярність прямих і площин ”.Теоретичний матеріал подано компактно, запропоновані зразки розв'язання і оформлення задач, таблиці для наочного сприйняття вивченого матеріалу, довідковий матеріал. При вивченні теоретичного матеріалу суттєво розвиваються просторові уявлення учнів. На прикладах геометричних фігур, які вивчаються, вони знайомляться із загальними поняттями перпендикулярності, вивчають питання взаємного розташування прямих, прямої і площини і площин, кутів та відстаней у просторі. Логічні і графічні вміння учнів розвиваються в ході розв'язування задач , які вимагають розпізнання різних випадків перпендикулярності, побудови відповідних малюнків.На уроках теми розглядаються зразки оформлення розв'язання задач з метою підготовки до зовнішнього незалежного оцінювання .

Перегляд файлу

Тематична папка використовується під час вивчення теми „ Перпендикулярність прямих і площин ”.

Вона побудована відповідно до чинної навчальної програми з математики та містить орієнтоване планування теми та детальні роздаткові та дидактичні матеріали до уроків. Матеріали папки переслідують головну мету: „Ввести систематизовані відомості про основні види перпендикулярності прямих і площин. Допомогти учням у вивченні матеріалу, результативному сприянню і усвідомленню нового матеріалу , набуттю навичок і умінь у розв’язуванні задач різного рівня складності.

Теоретичний матеріал подано компактно, запропоновані зразки розв’язання і оформлення задач, таблиці для наочного сприйняття вивченого матеріалу, довідковий матеріал. При вивченні теоретичного матеріалу суттєво розвиваються просторові уявлення учнів. На прикладах геометричних фігур, які вивчаються, вони знайомляться із загальними поняттями перпендикулярності, вивчають питання взаємного розташування прямих, прямої і площини і площин, кутів та відстаней у просторі.

Логічні і графічні вміння учнів розвиваються в ході розв’язування задач , які вимагають розпізнання різних випадків перпендикулярності, побудови відповідних малюнків.

Розроблено картки – завдання для самостійної роботи , картки – тести , картки – завдання зі зразками розв’язання задач, практичні роботи, в яких використовуються знання всієї теми ( показаний зв’язок предметів геометрія і технічне креслення , геометрії і виробничого навчання), завдання для тематичної атестації .

На уроках теми розглядаються зразки оформлення розв’язання задач з метою підготовки до зовнішнього незалежного оцінювання .

Майже на кожному уроці використовуються інноваційні технології навчання :

„ Ажурна пилка ” , „Інтерв’ю ” , „Мікрофон ”, „Незакінчене речення ”, а також традиційні методи навчання.

Дидактичні та роздаткові матеріали , які подаються в папці , несуть у собі такі ознаки інноваційності:

1) можливість диференційованого та індивідуального підходу до вивчення матеріалу;

2) розвиток творчих можливостей учнів та самостійності у добуванні знань, підготовки їх до олімпіад та вступу до вищих навчальних закладів. Ефективність дидактичного та роздаткового матеріалу :

1) матеріали дають змогу економити час на уроці ;

2) матеріали дають змогу раціонально використовувати 12 – бальну систему оцінювання навчальних досягнень учнів;

3) матеріали забезпечують засвоєння та поглиблення знань і способів дій на рівні їх застосування і у новій ситуації.

Головне значення перпендикуляра -

це його роль у техніці і в усьому нашому вжитку.

О.Д.Александров

Орієнтовний план вивчення теми

*Тема 2 Перпендикулярність прямих та площин (11 годин)*
1.	Кут між прямими. Перпендикулярність прямих у просторі.	§27
2.	Признак перпендикулярності прямих.	§27
3.	Перпендикулярність прямої і площини.	§28
4.	Ознака перпендикулярності прямої і площини.	§28
5.	Властивості прямих перпендикулярних до площини.	§28
6.	Перпендикуляр і похила. Розв’язування задач.	§29
7.	Теорема про три перпендикуляри.	§29
8.	Розв’язування задач.	§27-29
9.	Двогранний кут.	§33
10.	Розв’язування задач. Самостійна робота.	§
11.	Проміжна тематична атестація
*Перпендикулярність площин. Кути і відстані в просторі (11 годин)*
12.	Перпендикулярність площин. Ознака перпендикулярності площин	§30
13.	Властивості перпендикулярних площин	§30
14.	Ортогональне проектування	§31
15.	Відстань між площинами, від прямої до площини.	§32
16.	Розв’язування задач на знаходження відстані від точки до прямої, від точки до площини.	§32
17.	Відстань між паралельними та мімобіжними прямими.	§32
18.	Розв’язування задач.	§30-32
19.	Кути у просторі. Кут між прямими у просторі.	§33
20.	Кут між прямою та площиною. Кут між площинами.	§33
21.	Розв’язування задач.	§30-33
22.	Тематична атестація

ТЕМА «ПЕРПЕНДИКУЛЯРНІ ПЛОЩИНИ.

ОЗНАКА ПЕРПЕНДИКУЛЯРНОСТІ ПЛОЩИН»

I ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ:

Кожна правильна відповідь оцінюється в один бал

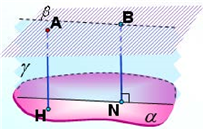
1. Скільки перпендикулярів можна опустити з даної точки до даної площини? Чому?

2. Скільки похилих можна провести з даної точки до даної площини? Чому?

3. Як слід установити на хрестовині ялинку, щоб вона була перпендикулярна до площини підлоги?

4. Як на практиці за допомогою виска перевірити вертикальність встановленого стовпа?

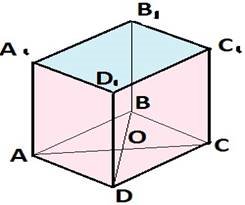
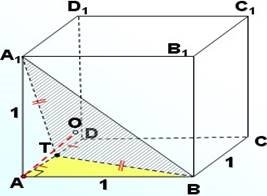
5. Знайти відстань від точки А до граней куба, якщо ребро куба дорівнює 10см.

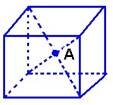
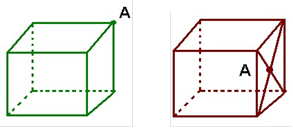
6. Чи можна стверджувати, що пряма, яка перетинає круг в центрі і перпендикулярна до двох діаметрів, перпендикулярна до площини круга?

7. Як розміщена пряма відносно площини трикутника, якщо вона перпендикулярна до двох його сторін?

8. Чи можуть бути перпендикулярними до однієї площини дві сторони трикутника?

9. Чи можуть бути перпендикулярними до однієї площини дві сторони трапеції?

10. Через точку, яка не лежить на прямій, побудуйте перпендикулярну до даної прямої площину.

2. По готовому домашньому завданню, раніше зробленому викладачем на дошці учні виконують самоперевірку, виставляють оцінку в зошит та лист самооцінки:

Задача 1.

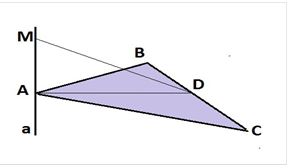
До площини квадрата АВСD, АВ = 2 дм, проведено перпендикуляр ВМ довжиною

4 дм. Знайти відстань від точки M до сторін АD і СD і діагоналі АС.

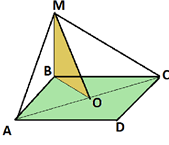Дано: АВСD — квадрат, АВ = 2 дм ВМ_⊥ (АВС), ВМ = 4 дм.

Знайти: МС і МА, МО.

Розв'язання.

1.СD ⊥ ВС, тому СD _⊥ МС. МС — шукана відстань від точки М до сторони СD.

АD _⊥ АВ, то АD _⊥ МА. Якщо ВС = ВА, то МС = МА.

2.Якщо МВ_⊥ (АВС), то МВ _⊥ ВС, МВ _⊥ ВА і МВ_⊥ ВD.

3.З ∆ МВС знайдемо МС: MC²₌BC²₊BM², MC²=2²+4²= 20 = 25 (дм), МА = МС = 25 дм.

4.АСIВD = О, АС⊥ ОВ, тоді АС⊥ ОМ (за теоремою про три перпендикуляри)

5.З ∆ АВС знайдемо АС: AC²₌AB²₊BC², АС = 2 2 (дм)

6.АС = ВD і ВО = AO, ВО = 2 (дм) З ∆ МВО знайдемо МО: 2

MO²= BO²+ MB², MO²= ( 2)²+ 4²= 2 +16 =18, MO = 3 2 (дм₎ Відповідь: МО = 3 2 дм, МС = МА = 25 дм.

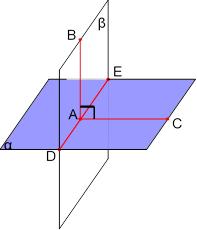
Кутом між площинами, які перетинаються, називається кут між прямими, проведеними в цих площинах перпендикулярно до лінії їх перетину.

Занотуй в зошит :

Які площини називаються перпендикулярними? Кут ВАС = 90°

Дві площини називаються перпендикулярними, якщо кут між ними дорівнює 90^o.

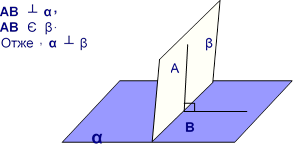
Сформулюйте ознаку перпендикулярності площин.

Якщо одна із двох площин проходить через пряму,

перпендикулярну до другої

площини, то такі площини перпендикулярні

Властивості перпендикулярних площин

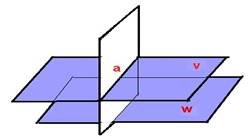
Площина, перпендикулярна до однієї з двох паралельних площин, паралельна і до другої площини.

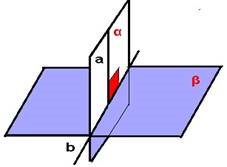
Якщо пряма, яка лежить в

одній із двох перпендикулярних площин,перпендикулярна до лінії їх перетину, то вона перпендикулярна і до другої площини.

a⊂_α,α⊥ _β,a _⊥b тоді b ⊥α

III МАТЕМАТИЧНИЙ ДИКТАНТ

Користуючись малюнком і назвіть:

1.Кут між двома площинами - це фігура? 2.У яких межах може змінюватись кут між площинами?

3.Чому дорівнює кут між паралельними площинами?

4.Які площина називаються перпендикулярними?

5.На скільки частин простір може поділитись трьома площинами, принаймні дві з них перпендикулярні?

6.Сформулюйте ознаку перпендикулярності площин.

IV ВЧИМОСЯ РОЗВ’ЯЗУВАТИ ЗАДАЧІ

Задача 1. II рівень

З точок Aі B , які лежать в перпендикулярних площинах попарно проведено перпендикуляри AC і BDдо прямої перетину площин. Знайдіть довжину відрізка AB , якщо AC = 3 см, BD ₌ 4 см, CD=2 см.

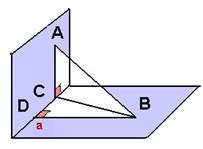
Дано:

α⊥ _β, A⊂_α,B ⊂ _βAC ⊥_α, BD ⊥ _β

АС = 3 см, BD = 4 см,

СD=12см

Знайти: АВ

РОЗВ'ЯЗАННЯ.

З _∆CDB(_∠D ₌90^o) за теоремою Піфагора знайдемо ВС: BC²₌BD²+ _СD²,

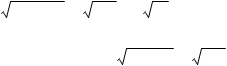BC = 16 +144 = 160 = 4 10 . Оскільки площини _α та _β перпендикулярні і AC _⊥CD, то ∠ACB = 90^o. Тоді за теоремою Піфагора з _∆ACB знайдемо AB:

AB²= AC²+ СB²AB = 9 +160 = 169 =13_.Отже,AB= 13c_м. Відповідь: AB= 13cм.

Задача 2. Ш рівень

(з обґрунтуванням кожного зробленого кроку )

Площини квадратів ABCD і ABC₁D_! лежать в перпендикулярних площинах, AB ₌a.

Знайдіть: а) відстань CC₁; б) відстань C₁D ; в) кут між діагоналями AC і AC₁.

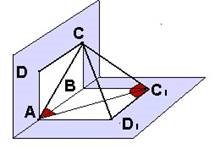Дано:

(ABCD)⊥ (ABC₁D₁), AB=a.

____________________

Знайти: CC₁, C₁D , ∠CAC₁

РОЗВ'ЯЗАННЯ.

1.Так якα⊥ β,тоді BC ⊥ BC1. Тоді з ∆CBC1: CC12 = BC12 + BC2 , CC12 = a2 + a2 = 2a2, CC₁= a2 .

2. ABC₁D_! - квадрат, звідки BC₁⊥ C₁D₁. BC₁- проекція похідної CC₁ на площину _β.

CC₁⊥ C₁D( за теоремою про три перпендикуляри). ²D₁C²+ CC₁², CD₁²= a²+ (a2)2 = 3a²CD₁= a3 .

3. З ∆СC₁D: по теоремі Піфагора CD₁=

4. Так як за умовою ABCD = ABC₁D_!, тоді AC ₌AC₁, AC₁²= AD₁²+ D₁C₁²= a²+ a²= 2a².

AC = AC₁= 2 a . Отже _∆ACC₁- рівносторонній∠A = ∠C = ∠C₁= 60^o, тобто ∠CAC₁=60 ◌ْ

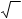
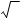Відповідь: CC₁= a2 , CD₁= a3 , ∠CAC₁=60 ◌ْ

V АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ

Вправа «Прес»

Завдання. Пояснити, використовуючи схему методу «Прес» :

«Я вважаю, що …»

«Тому що …»

«Наприклад …» «Отже …».

1. Чи кожна трійка попарно перпендикулярних площин має спільну точку? Чи мають вони спільну пряму?

2. Чи існує чотири попарно перпендикулярні площини?

3. Чи можуть бути не перпендикулярними дві площини, які проходять через дві перпендикулярні прямі?

4. Чи правильно, що дві площини, перпендикулярні до третьої, паралельні?

5. Дано площину_α і точкуA. Скільки існує площин, перпендикулярних до _α , які проходять через точку A?

6. Чи кожна трійка попарно перпендикулярних площин має спільну точку? Чи мають вони спільну пряму?

7. Чи можуть бути перпендикулярними дві прямі, які паралельні одній площині?

8. Скільки можна провести прямих, одночасно перпендикулярних до двох мимобіжних прямих?

9. Пряма, яка проходить через середини основ трапеції, перпендикулярна до площини β. Тоді середня лінія трапеції …

10. Через кожну з двох мимобіжних прямих проведено площину.

Тоді ці площини …

Самостійна робота 1

(Робота в парах , перевір свого сусіда по парті і постав оцінку)

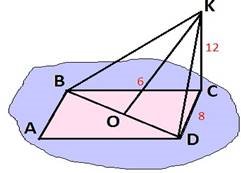
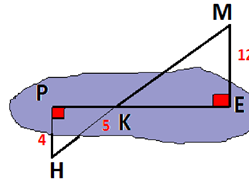
I варіант На рис. зображено прямокутник ABCD. CD = 8 см; ВС = 6 см; KC = 12 см. KC⊥CD, KC⊥ВС.

Запитання. Чи є правильним, що: Відповідь:
1. КС⊥(ABC)
2. КС⊥AC
3. АС = 10 см
4. ОК = 14 см
5. ОК – висота, проведена до BD у трикутнику BКD
6. ОК – медіана в трикутнику ВКD
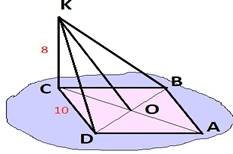
	II варіант На рис. зображено ромб ABCD. KС ⊥
	(ABC). CD = 10 см, ВD = 12см, KС = 8см
Запитання. Чи є правильним, що:	Відповідь:
1. ОК – висота, проведена до BD у трикутнику BКD
2. ОС = 6 см
3. ОК = 82
4. КС⊥(ABC)

5. КС⊥AC
6. AC _⊥BD

VІ ЗАКРІПЛЕННЯ ВИВЧЕНОГО МАТЕРІАЛУ

ПЕРЕВІР СЕБЕ! ІНДИВІДУАЛЬНА РОБОТА

ТЕСТ

№	ВАРІАНТ ВІДПОВІДІ
	А	Б	В
1	Якщо дві площини перпендикулярні, то …
	Кут між ними дорівнює 90^º	Усяка пряма однієї площини перпендикулярна до іншої площини	Лінія їх перетину перпендикулярна до обох площин
2	Чи вірно, що довільна пряма, яка лежить в одній з двох взаємно перпендикулярних площин, перпендикулярна до іншої площини?
	Так, завжди	Ні, ніколи	Інколи, таке можливо
3	Паралельні прямі а і в лежать в одній площині β. Через кожну з цих прямих проведено площину, перпендикулярну до даної площини β. Як розміщені ці площини одна відносно другої?
	Площини паралельні	Площини перетинаються	Площини перпендикулярні
4	Скільки площин, перпендикулярних до площини γ, можна провести через пряму с, яка перпендикулярна до даної площини γ?
	Тільки одну площину	Безліч	Жодної
5	Чи правильно, що через похилу до площини не можна провести площину, перпендикулярну до цієї площини?
	Так, вірно. Таку площину не можна провести ніколи	Ні, невірно. Можна провести площину завжди	Інколи таку площину можна провести
6	Яку найбільшу кількість попарно перпендикулярних площин можна розмістити в просторі?
	Чотири	Безліч	Три
7	Скільки площин, перпендикулярних до площини β, проходить через пряму в, що не є перпендикулярною до площини β?
	Одна	Жодна	Безліч
8	Якщо дві площини перпендикулярні до третьої площини, то лінії їх перетину з цією площиною …
	Паралельні	Перетинаються	Паралельні або перетинаються
9	Площина α перпендикулярна до площини β, а площина β перпендикулярна до площини γ. Тоді площини α і γ розміщені так:
	Перетинаються або перпендикулярні	Перпендикулярні або паралельні	Можливе будь – яке розміщення
10	Чи може перпендикуляр до площини, проведений з кінця похилої, дорівнювати її проекції на цю площину?
	Так, таке можливо	Ні, ніколи	Так, завжди

Інтерактивна вправа: робота в малих групах.

Учні об’єднуються у три різнорівневі групи. Кожна група отримує завдання відповідного рівня складності. Учні записують розв’язки у зошит, а один представник від групи працює біля дошки

Група 2
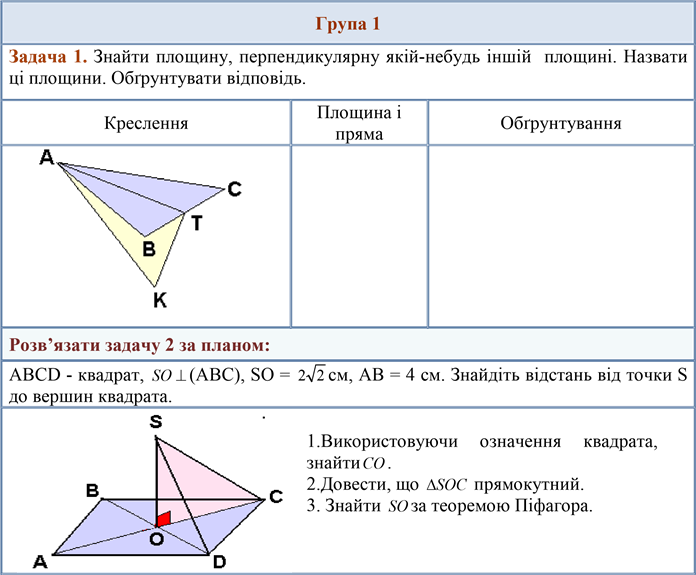
Задача 1. Знайти пряму, перпендикулярну якій-небудь площині. Назвати ці пряму і площину. Обґрунтувати відповідь.
Креслення	Площина і пряма	Обґрунтування

Розв’язати задачу 2 за планом:
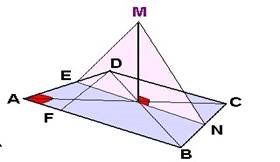
Пряма а перпендикулярна площині ∆ABC , BD=CD і MD відрізок, який сполучає довільну точку прямої а і перпендикулярний до BC .Довести, що AB=AC .
1. MD⊥¹BC^.⇒MD⊥ AD (наслідок теореми про три перпендикуляри) 2.Розглянути _∆ADB і _∆ADC - довести їх рівність.

Група 3
1.	Задача 1.Знайти площину, яка перпендикуляра до площини AA₁B₁B; ABCD; проекцію похилої C₁O на площину ABC . Обґрунтувати відповідь.
	Креслення	Площина і пряма	Обґрунтування

Розв’язати задачу 2 за планом:

Прямокутна трапеція з гострим кутом в 45° і більшою бічною стороною, яка дорівнює 6 2 см, розташована на площині α. На відстані 4 см від площини _α знаходиться точка, рівновіддалена від кожної сторони трапеції. Знайдіть відстань від цієї точки до сторін трапеції.

1. Довести, що Δ ADK прямокутний.

2.Використовуючи означення синуса гострого кута в Δ ADK , знайти AK . 3. Довести, що _∆MOE прямокутний.

4.За теоремою Піфагора знайти ME ₌MN .

VI Рефлексія Учням пропоную висловитися з питання:

1.Розвитку яких рис характеру сприяв урок (самостійності, спостережливості, відповідальності).

2.Чи отримали ви задоволення від власної праці?

3.Чи вичерпали ви свої можливості?

4.Що тобі сподобалось на уроці?

5.Порівняйте свої знання на початку уроку і в кінці

VII Домашнє завдання

§30, контрольні запитання №1-5

задачі № 1083,1092

Якщо є вільний час. Кросворд.

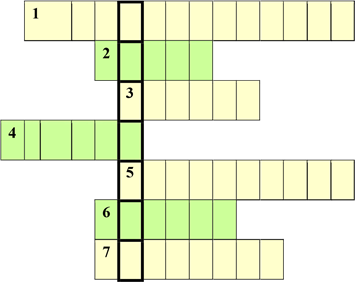
1. Найкоротша відстань від точки до площини…

2. Похилі, які мають рівні проекції, …

3. Трикутник це геометрична …

4. Кінець перпендикуляра, що лежить у площині…

5. Одна із сторін прямокутного трикутника…

6. Відрізок, який сполучає дану точку, з точкою площини, але не перпендикуляр.

7. Відрізок, що сполучає основи перпендикуляра і похилої, проведених з однієї точки…

Ключове слово: ?

ТЕМА «ОРТОГОНАЛЬНЕ ПРОЕКТУВАННЯ»

I ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ

ІНТЕРАКТИВНА ВПРАВА « ^ІНТЕРВ`Ю»

(Одна правильна відповідь оцінюється в 1 бал) 1) Які площини називаються перпендикулярними?

2) Сформулюйте ознаку перпендикулярності площин.

3) Як розташована пряма, яка лежить в одній із двох перпендикулярних площин і перпендикулярна до лінії перетину цих площин, відносно другої площини?

4) Сформулюйте узагальнене означення перпендикулярності прямої і площини.

5) Сформулюйте узагальнену ознаку перпендикулярності прямої і площини.

6) Сформулюйте узагальнену теорему про три перпендикуляри.

7) Дайте означення кута між прямою і площиною.

8) В яких межах знаходиться кутова міра кута між прямою і площиною?

9) Дайте означення кута між площинами.

10) Чи залежить величина кута між площинами від вибору січної площини?

Самостійна робота 1

(Робота в парах , перевір свого сусіда по парті і постав оцінку)

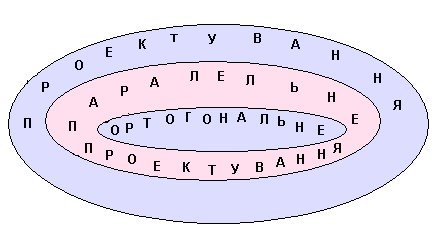
II Теоретичний матеріал до уроку

Занотуй в зошит:

Якщо проектуючи прямі перпендикулярні до площини проекцій, то таке проектування називається прямокутним, або ортогональним проектуванням. Ортогональне проектування – окремий вид паралельного проектування, тому воно має всі властивості паралельного проектування.

Властивості ортогонального проектування:

– Прямолінійні відрізки фігури зображуються на площині малюнка прямолінійними відрізками. – Паралельні відрізки фігури зображуються на площині малюнка паралельними відрізками, або відрізками, що лежать на одній прямій.

– Відношення відрізків однієї прямої або паралельних прямих зберігається при ортогональному проектуванні.

Теорема

Площа проекції многокутника дорівнює площі проектованого многокутника, помноженого на косинус кута між ними:

S_ПР= S cosϕ

Наслідок

Якщо S i Q – площі многокутників площини α, а S_пр i Q_пр- площі їх проекцій на площину α, то

S_пр:Q_пр=S :Q

ЗЛІД ЗАПАМ`ЯТАТИ

III РОЗВ`ЯЗУВАННЯ ЗАДАЧ

(з обґрунтуванням кожного зробленого кроку)

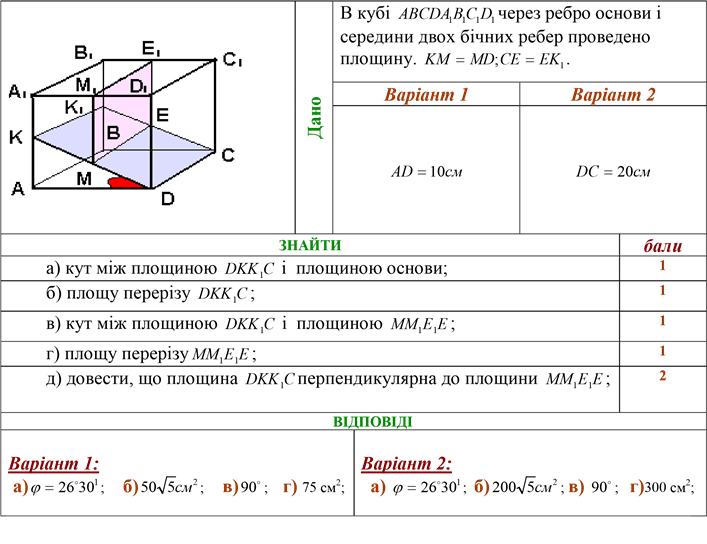
Задача 1. ІІI рівень (розв’язування за планом)

Кут між площиною рівнобедреного трикутника ABC і його ортогональною проекцією ABC¹дорівнює 60° (АВ - спільна основа трикутників). Знайдіть відстаньміж точкою С і стороною AB та площу проекції -_∆ACB, якщо АС = 15 см, AC¹ =10 см.

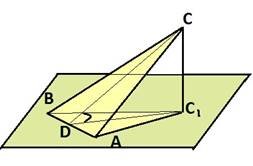
Пояснення до малюнка.

Трикутники ABC і ABC¹ рівнобедрені, тоді АС= ВС і АC¹=ВC¹. ∠ϕ₌60^o-кут між площинами даних трикутників.

Мал.1 План розв’язання.

1. DC1– ¹проекція60° DC на площину α 7. S∆AC1B = 12 DC1 × AB

2. ∠CDC =ϕ=

¹CC¹⊥ (< ABC¹) , 8. Обчислити : 1) СС¹з < ACC¹;

3. CC ⊥α⇒

2) CDз∆CC¹D;

4. AC=BC⇒CD⊥ AB

_5._AD₌_DB_,_AB₌_2AD 3) DC¹ з ∆CDC¹;

4) AD з ∆ADB

_6.^AD⁼^AC²⁻^DC² 5) S_∆_AC1_B

Розв’язання._____________________________________________________________ ________________________________________________________________________

________________________________________________________________________ ________________________________________________________________________

________________________________________________________________________

Відповідь : 1. CD= 10 53см 2. S∆ABC1 = 503 37см2

Задача 2.ІІ рівень

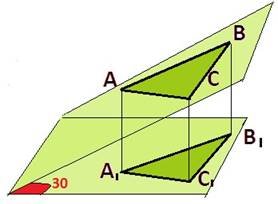
Ортогональною проекцією ∆ABC є прямокутний трикутних А₁В₁С₁ з гіпотенузою

15 см і різницею катетів 3 см. Знайдіть площу даного трикутника, якщо кут між площинами дорівнює 30º.

Розв’язання .

Мал.2

Для розв’язання задачі використаємо малюнок 2.

∆ А В С (∠С = 90^o) - ортогональна

_{1 1 1 1}

проекція ∆ABC. Нехай А₁С₁= x, тоді

В₁С₁=x+3. За теоремою Піфагора

A1B!2 = A1C12 + B1C12, x2 + (x + 3)2 = 225, x²+ x²+ 6x + 9 = 225, 2x²+ 6x − 216 = 0, x²+ 3x −108 = 0 ; x₁= 9, x₂=−12 .

Отже, А₁С₁= 9 см, тоді В₁С₁= 12 см.

S× B₁C₁, тобто

S Тоді площа ∆ABC:

S¹_o,Відповідь: S_<_ABC= 363(cм²)

S ₌

cos30

VI АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ

„РОБОТА В ПАРАХ ”

Учні об’єднуються парами , відповідають на питання , поставлені один одному , таким чином готуються до виконання навчальної самостійної роботи : один учень відповідає на питання парних номерів списку , а інший – непарних .

	ЗАВДАННЯ
1.	ABCDABCD Відомо, 1 1 1 1 - ^куб. Знайдіть ортогональні проекції діагоналі BD на грань: а); ABCD; б) A1B1C1D1; в) DD1C1C ; г) ADD!A1	1
2.	Сформувати властивості ортогонального проектування	1
3.	Точки К і М середини ребер АВ і DС трикутної піраміди DАВС, кожне ребро якої дорівнює а. Доведіть, що КМ⊥ АВ . Знайдіть довжину відрізка КМ.	1
4.	У кубі ABCDA₁B₁C₁D₁ проведено переріз січною площиною, яка проходить через точки A₁B₁CD. Вкажіть, які з наведених тверджень правильні, а які - неправильні: а) площина A₁DB₁ перпендикулярна до прямої AA₁; б) кут між прямою АD і площиною дорівнює 45° ; в) кут між прямою АВ і січною площиною дорівнює 0°; г) кут між прямою BC₁ і площиною дорівнює 90°	1
5.	Як задається паралельна проекція?	1
6.	Як побудувати ортогональну проекцію фігури?	1
7.	Наведіть приклади перпендикулярних площин із оточення.	1
8.	На двох перпендикулярних площинах вибрали по прямій. Чи може статися, що ці прямі: а) паралельні; б) перетинаються; в) мимобіжні?	1
9.	Чи зберігаються при ортогональному проектуванні довжини відрізків, величини кутів?	1
10.	Площина α перпендикулярна до площини β, а площина β перпендикулярна до площини γ. Тоді як розміщені площини α і γ?	1

ПЕРЕВІР СЕБЕ! САМОСТІЙНА РОБОТА

Учням пропонується розв’язати завдання різної складності. Завдання оцінюються у 3 бали. Учні самі обирають завдання і розв’язують його напротязі 15 хвилин.

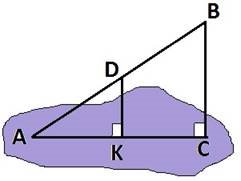
	Задача 1. Через кінець Aвідрізка AB проходить площина. Точка B знаходиться від неї на відстані 16см. Знайти відстань від середини відрізка AB до площини. *Виберіть правильну відповідь:* А) 8 Б) 12 В) 10 Г) 4 Допомога: DK ⊥ AC , BC ⊥ AC , за теоремою Фалеса DK - середня лінія ∆ABC .
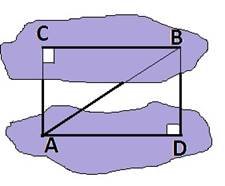
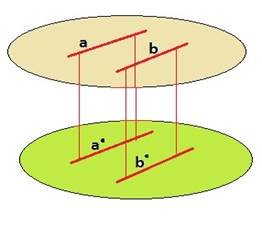
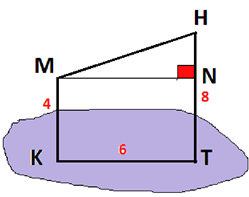
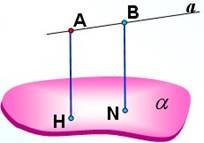
	Задача 1. Відрізок довжиною 10см своїми кінцями спирається в дві паралельні площини, відстань між якими дорівнює 8 см. Знайти проекцію відрізка на площини. *Виберіть правильну відповідь:* А) 6 і 6 Б) 6 і 5 В) 8 і 8 Г) 8 і 5 Допомога: За теоремою Піфагора BC = AB²− AC² і AD=BC.
	Задача 1. Через кінці відрізкаMH проведені прямі, які перпендикулярні до площини і перетинають її в точкахKiT відповідно. Знайти MH , якщо KT = 6,MK = 4,HT = 8 і точки MiH знаходяться по одну сторону від площини. *Виберіть правильну відповідь:* А) 29 Б) 28 В) 8 Г) 41 Допомога: За теоремою ПіфагораMH = MN ²+ HN ²
	Задача 1. ВідрізокMH перетинає площину в точці K . Через кінці відрізка проведені прямі HPі ME , які перпендикулярні до площини і перетинають її в точках P E . Знайти, якщо HP = 4,HK = 6,ME =12 *Виберіть правильну відповідь:* А) 8 Б) 3 В) 12 Г) 1 Допомога: За теоремою ПіфагораPK ²= HK ²+ PH ² ∆PKE∞∆MKE _,^KE= ^ME⇒ KE = 3⋅12 PK PH 4

Відповісти на запитання Вправа «Рюкзак»

Завдання

1. Відповісти на запитання

2. Скласти відповіді у рюкзак

Я взнав:	*Сьогодні на уроці*
1.	________________________________
2.	________________________________
3.	________________________________
4.	________________________________
5. Я навчився:	________________________________
1.	________________________________
2.	________________________________
3.	________________________________
4.	________________________________
5.	________________________________

VI Домашнє завдання

§31, контрольні запитання №1-5

задачі № 1115,1134

Практичне завдання.

Побудуйте проекцію діагоналі основи куба на площину, яка проходить через дві діагоналі його суміжних бічних граней. Знайдіть довжину проекції, якщо довжина діагоналі d.

ТЕМА «ВІДСТАНЬ МІЖ ПЛОЩИНАМИ,

ВІД ПРЯМОЇ ДО ПЛОЩИНИ»

I ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ

Вправа «Розумний куб»

1. Як розміщені прямі у просторі, якщо їх ортогональні проекції на площину – прямі, що перетинаються (паралельні)?

2. Які фігури можуть бути ортогональними проекціями двох паралельних прямих (двох мимобіжних прямих)?

3. Чи може ортогональною проекцією правильного тетраедра на площину бути рівнобедрений трикутник (рівносторонній трикутник)?

4. Що зміниться, якщо сторона трикутника не належатиме площині, а буде паралельною їй?

5. Чи може площа ортогональної проекції многокутника дорівнювати площі даного многокутника? Коли це можливо?

6. Від чого залежить те, на скільки зменшується площа многокутника при ортогональному проектуванні?

МЕТОД «НАВЕДИ ПОРЯДОК»

Записуємо на дошці розв’язання домашньої задачі з пропусками. Два учні заповнюють пропуски і пояснюють хід міркувань. Під час розгляду розв’язання завдань зошити в учнів закриті. Після закінчення пояснення кожен учень перевіряє свою роботу за зразком, підкреслює помилки..

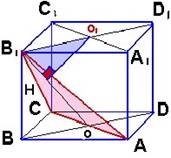
Задача.В кубі ABCDA₁B₁C D₁ знайти відстань від точкиC₁ до площини(AB₁C₁), ребро якого дорівнює 1.

Дано:

ABCDA₁B₁C D₁- куб, AB =1

Знайти: d(C₁;(AB₁C₁)) Пояснення до малюнку:

C₁⊂ A₁C₁, A₁C₁C(AB₁C), отже відстань від точки C₁до площини (AB₁C₁)дорівнює

Мал.1 відстані від довільної точки відрізка A₁C₁ до (AB₁C₁), наприклад від точкиO₁.

РОЗВ'ЯЗАННЯ.

1.O₁H ⊥ B₁O(чому?) , O₁H ⊥ AC(чому?). Так як AC ⊥ (BB₁D₁),O₁H ⊂ (BB₁D₁)⇒ O₁H ⊥ (AB₁C) і d(O₁;(AB₁C))=O₁H .

2.З ∆B₁A₁D₁: за теоремою Піфагора B,

3. З ∆B₁O₁O : B₁O₁⊥ O₁O , ( яка використана теорема?) OB, OB₁²= ⊗ + ^_ 2²^_=_⊗

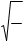OB₁= ³;

4. . З іншого боку: S;

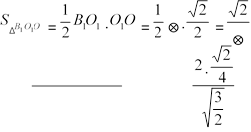O1H = ⊗⋅S(∆B1O1O); O1H = = ⊗⋅⊗ = 1 = ⊗ . Відповідь : O1H =3 . B₁O 3 3

II Теоретичний матеріал до уроку

ПРОЕКТНЕ ЗАВДАННЯ

Учням пропонується виділити в зошиті чисту сторінку для складання схемипроекту, де робляться записи в процесі роботи на уроці.

Група розподіляється на три підгрупи. Перша складає проект з теми «Відстань між прямими» , друга складає проект з теми «Відстань між прямою та площиною», а третя - «Відстань між площинами».Наприкінці уроку учні обговорюють схему, яку накреслили під час роботи на уроці.

Занотуй у зошит:

Відстань між двома фігурами називають відстань між найближчими точками цих фігур(якщо такі існують)

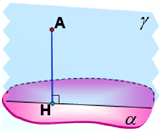
Відстань від точки до площини дорівнює довжині перпендикуляра, опущеного із даної точки на площину

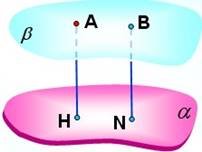
Відстань між паралельними площинами є довжина перпендикуляра, опущеного з будь-якої

точки площини на паралельну їй площину

Відстань між двома мимобіжними прямими

дорівнює довжині їх спільного перпендикуляра

Дві мимобіжні прямі визначають пару паралельних площин. Відстань між цими площинами дорівнює відстані між даними прямими

III ЗРАЗКИ РОЗВ'ЯЗАННЯ ЗАДАЧ

Вчимося розв’язувати задачі

Задача 3. Ш рівень

(з обґрунтуванням кожного зробленого кроку )

Дано куб ABCDA₁B₁C₁D₁. Довжина ребра куба дорівнює 1. Найти відстань від середини відрізка BC₁ до площини AB₁D₁

Алгоритм розв`язування задачі:

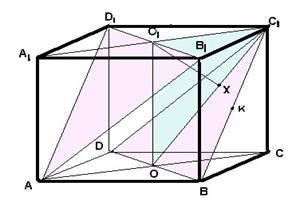1.Через точки A,B₁iD₁ проводимо площину α, а через точки D,BiC₁площину_β, причому_β II _α.

2.Будуємо третю площину, перпендикулярну паралельним площинам _α і _β.

3.На лінії перетину площин вибираємо точку O₁ і опускаємо перпендикуляр із точкиO₁.

4. Відрізок O1X – відстань між площинами рівна відстані від точки K до площини _α. Мал.1

РОЗВ'ЯЗАННЯ.

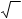
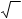
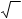1. З ∆ABC : AC2 = AB2 + CB2, AC 2 =12 +12 = 2, AC = ± 2, AC = 2 , тоді C1O1 = CO = 2

2. З ∆CC1O :C1O2 = CC12 + CO2 ,C1O2 =12 +  22  =112 = 23 , C1O = ± 23 ,C1O = 23 .

3.Щоб знайти відстань від середини відрізка BC₁ до площини AB₁D₁, яка дорівнює висоті O₁X₁, виразимо двічі площу ∆OC₁O₁:

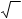
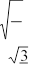
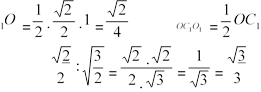SOC1O1 = 12 O1C1 ×O ; S ×O1 X , 42 = 12 ⋅ 23 ⋅O1X /× 2,

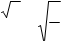22 = 23 ×O1X , O1X = . Відповідь: O1 X = 3

Задача 2. IV рівень

Дано рівносторонній трикутник_∆ABC зі стороною 2. В просторі взяли точкуD таку, що AD = BD = 2, CD=1.Найти відстань від точкиD, до плошини _∆ABC.

Дано:

∆ABC, AB₌BC ₌AC ₌2, Мал.2 AD = BD = 2, CD=1

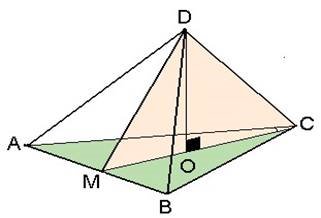Знайти: DO

Пояснення до малюнку: Відстань DO - це висота піраміди DABC. Нехай M - середина AB . Проведемо DO на пряму CM .

РОЗВ'ЯЗАННЯ.

1. CM є медіаною, а значить і висотою ∆ABC, тоді AB ⊥ CM ; AB ⊥ DM , тобто ∆ABD - рівносторонній;

2. AB ⊥ (MDC), отже AB ⊥ DO;DO ⊥ CM (за побудовою)і DO ⊥ AB ⇒ DO ⊥ (ABC)

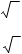
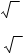3.З _∆BCM : CM ²= BC²− MB², СM ²= 2²−1²= 3, CM ²= ± 3 , СM = 3 ; 4.З ∆BDM : DM²= BD²− MC², DM²= 2²−1²= 3, DM = ±3, DM =3 ;

5. З _∆DMC по теоремі косинусів: DM ²= DC²+ СM ²− 2⋅ DC ⋅MC ⋅cosϕ, (де ϕ= _∠DCM)

;

6.З _∆DOC: cos_ϕ₌^OC; OC ₌DC _⋅cos_ϕ, OC ₌1_⋅³; DO²₌DC²₋OC²;

DC 6

DO2 =1−  63  =1−=; DO = 633 . Відповідь: DO = 633



IV ЗАКРІПЛЕННЯ НАБУТИХ ЗНАНЬ

«Ажурна пилка»

Зразки карток з диференційованими завданнями.

Картка – завдання з друкованою основою (чотири варіанта )

I варіант

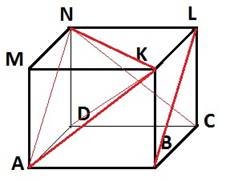
1. Дано зображення куба. Ребро куба дорівнює а

1.Знайдіть відстань між прямими:

1) AB і LK 2) AK і CN 3) AN і KM 4) DL і AB 5) AL і BK 6) KN і AB

2.Знайдіть ортогональні проекції відрізка BL на площину:

а)АВС; б) DLC; в) MNK; г)ADL; к)АВМ;

е) ВСК.

II варіант

2. Дано зображення прямокутного паралелепіпеда, лінійні виміри якого дорівнюють 1×2×3

1.Знайдіть відстань між прямою і площиною:

1) AD₁і (BB₁C₁C) 2) D₁B₁ і(ABCD)

3) AB₁і (DD₁C₁C) 4) B₁C і (CC₁D₁D)

III варіант

3.Через вершину А прямокутника ABCD проведено перпендикуляр SA до площини прямокутника. Відомо, що АВ = 1 см, AD = 3 см. Укажіть, які з наведених тверджень правильні, а які — неправильні:

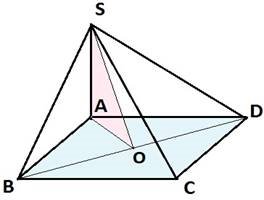
а) спільним перпендикуляром прямих SA і DC є відрізок AD;

б) відстань між прямими SA і ВС менша 3 см;

в) відстань між прямими SA і BD дорівнює відстані між точкою А і прямою BD;

IV варіант

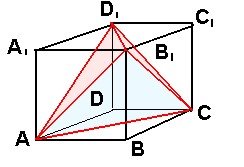
4. Користуючись зображенням куба

ABCDA₁B₁C₁D₁, укажіть:

а) пряму, яка перпендикулярна до площини BB₁D; ACC₁;

б) лінійний кут двогранного кута з гранями ACD₁і ACD; ACB₁і ACB ;

в) площину, яка перпендикуляра до площини AA₁B₁B; ABCD;

г) проекцію похилої D₁O на площину ABC

V Систематизація та узагальнення знань:

Метод «Незакінчене речення»

1. Якщо дві прямі перетинаються у просторі, то вони утворюють...

2. Відстань між даними прямими - це...

3. Кут між прямими - це не фігура, а...

4. Відстань між мимобіжними прямими - це...

5. Дві прямі називаються перпендикулярними, якщо...

6. Перпендикуляром, опущеним з даної точки на площину, називається відрізок...

7. Відрізок, який сполучає дану точку з точкою площини і не є перпендикуляром, називається...

8. Рівні похилі мають...

9. Проекція - це...

10. Відстань між площинами-це…

ЗАПОВНІТЬ ТАБЛИЦЮ ТА ПРОАНАЛІЗУЙТЕ РЕЗУЛЬТАТИ:

	Дано куб ABCDA₁B₁C₁D₁, довжина ребра якого дорівнює 1. Проведено переріз через середину грані AD точкуT та вершини A₁_іB .
Питання	Обґрунтування , обчислення.
1. Переріз A₁TB– трикутник. Який?
2. Якщо АТ=ТD ; то TA₁=TB
3. ∠A₁TB =180°− 2_β
4. Якщо AA₁⊥ (ABCD)то∆ATB − прямокутний
5. O_∉(ABCD)
6. З ∆A₁AT : A₁T − ? S(∆A₁AT) − ?
7. пл.(AA₁D₁D)⊥ пл.∆(A₁TB)− ?
8. Назвати ребра, перпендикулярні до грані ABB₁A₁
9. Назвати площини, перпендикулярні до площини перерізу.

Самостійна робота по варіантам.

Таблиця варіантів

варіант	задачі	рівні
І	1,3	А*
ІІ	2,4	А*
ІІІ	3,6	Б*
ІV	4,5	Б*

А* - завдання відповідають програмним вимогам, Б* - завдання призначені для учнів, які виявляють підвищений інтерес до математики.

	№ з/п	Завдання
	1	Ребро куба дорівнює а. Знайти площу перерізу куба площиною, яка проходить через вершину основи під кутом 30⁰ до цієї основи і перетинає всі бічні ребра.
	2	Знайти площу многокутника, якщо площа його ортогональної проекції 50см², а кут між площиною многокутника і площиною його проекції дорівнює 45⁰.
	3	З точки , що віддалена від площин на відстань 5 см, проведено дві похилі , які утворюють із площиною кути 45º, а між собою кут-60º . Знайти відстань між кінцями похилих .
	4	Прямокутна трапеція з гострим кутом в 45° і більшою бічною стороною, яка дорівнює 6 2 см, розташована на площині α. На відстані 4 см від площини _α знаходиться точка, рівновіддалена від кожної сторони трапеції. Знайдіть відстань від цієї точки до сторін трапеції.
	5	Точка, однаково віддалена від всіх сторін рівнобічної трапеції, знаходиться на відстані 3 см від її площини. Периметр трапеції дорівнює 48 см. Знайдіть відстань від точки до сторін трапеції.
	6	Ортогональною проекцією правильного трикутника зі стороною 20см на площину, паралельну одній із сторін, є рівнобедрений трикутник , одна із сторін якого дорівнює 5 13 см. Знайдіть кут між площинами трикутників.

VI Рефлексія

Учням пропоную висловитися з питання:

1. Розвитку яких рис характеру сприяв урок (самостійності, спостережливості, відповідальності).

2. Якого життєвого досвіду ви набули (володіти собою, захищати свої знання, бути впевненими в собі).

3. Чи отримали ви задоволення від власної праці?

4. Чи вичерпали ви свої можливості?

5. Що ти хотів би змінити під час уроку?

VII Домашнє завдання

§32, контрольні запитання, задачі № 1141,1134

Середня оцінка розробки

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0

Загальна:

5.0

Всього відгуків: 1

Оцінки та відгуки

Огородник Надя 15.04.2020 в 09:41

Загальна:

5.0

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0

pdf

Завантажити

Зберегти на потім

Додав(-ла)

Ляхова Тетяна Петрівна

Пов’язані теми

Геометрія, 10 клас, Розробки уроків

Додано

18 листопада 2018

Переглядів

24565

Оцінка розробки

5.0 (1 відгук)

ОЗНАКА ПЕРПЕНДИКУЛЯРНОСТІ ПЛОЩИН»

АС = 3 см, BD = 4 см,

(з обґрунтуванням кожного зробленого кроку )

____________________

Відповідь: CC1 = a2 , CD1 = a3 , ∠CAC1 =60 ◌ْ

(Робота в парах , перевір свого сусіда по парті і постав оцінку)

Самостійна робота 1

Задача 1. ІІI рівень (розв’язування за планом)

4. AC=BC⇒CD⊥ AB

S× B1C1 , тобто

„РОБОТА В ПАРАХ ”

ПЕРЕВІР СЕБЕ! САМОСТІЙНА РОБОТА

Відповісти на запитання Вправа «Рюкзак»

Завдання

VI Домашнє завдання

Вправа «Розумний куб»

ABCDA1B1C D1- куб, AB =1

OB1 = 3 ;

II Теоретичний матеріал до уроку

ПРОЕКТНЕ ЗАВДАННЯ

III ЗРАЗКИ РОЗВ'ЯЗАННЯ ЗАДАЧ

(з обґрунтуванням кожного зробленого кроку )

1. З ∆ABC : AC2 = AB2 + CB2, AC 2 =12 +12 = 2, AC = ± 2, AC = 2 , тоді C1O1 = CO = 2

SOC1O1 = 12 O1C1 ×O ; S ×O1 X , 42 = 12 ⋅ 23 ⋅O1X /× 2,

22 = 23 ×O1X , O1X = . Відповідь: O1 X = 3

∆ABC, AB= BC = AC = 2, Мал.2 AD = BD = 2, CD=1

Знайти: DO

3.З ∆BCM : CM 2 = BC2 − MB2, СM 2 = 22 −12 = 3, CM 2 = ± 3 , СM = 3 ; 4.З ∆BDM : DM2 = BD2 − MC2, DM2 = 22 −12 = 3, DM = ±3, DM =3 ;

DC 6

«Ажурна пилка»

Таблиця варіантів

Відповідь: CC₁= a2 , CD₁= a3 , ∠CAC₁=60 ◌ْ

S× B₁C₁, тобто

ABCDA₁B₁C D₁- куб, AB =1

OB₁= ³;

∆ABC, AB₌BC ₌AC ₌2, Мал.2 AD = BD = 2, CD=1

3.З _∆BCM : CM ²= BC²− MB², СM ²= 2²−1²= 3, CM ²= ± 3 , СM = 3 ; 4.З ∆BDM : DM²= BD²− MC², DM²= 2²−1²= 3, DM = ±3, DM =3 ;