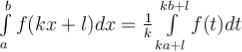"Первісна та інтеграл"


![]()

Первісна та інтеграл
Первісна
Означення: Функція ![]() називається первісною для функції
називається первісною для функції ![]() на даному проміжку, якщо для будь-якого
на даному проміжку, якщо для будь-якого ![]() з цього проміжку
з цього проміжку ![]()
q Приклади
-
Для функції
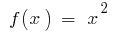 на інтервалі
на інтервалі 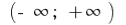 первісною є
первісною є 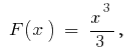 оскільки
оскільки 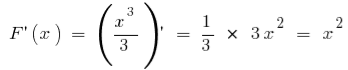
-
Для функції
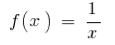 на інтервалі
на інтервалі  первісною є
первісною є 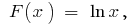 оскільки
оскільки 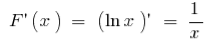
Основна властивість первісних
Якщо функція ![]() є первісною для функції
є первісною для функції ![]() на даному проміжку, а
на даному проміжку, а ![]() — довільна стала, то функція
— довільна стала, то функція ![]() також є первісною для функції
також є первісною для функції ![]() при цьому будь-яка первісна для функції
при цьому будь-яка первісна для функції ![]() на даному проміжку може бути записана у вигляді
на даному проміжку може бути записана у вигляді ![]() де
де ![]() — довільна стала
— довільна стала
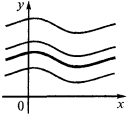
Геометричний зміст
Графіки будь-яких первісних даної функції одержуються один з одного паралельним перенесенням уздовж осі ![]()
Невизначений інтеграл
Означення:Сукупність усіх первісних даної функції ![]() називається невизначеним інтегралом і позначається символом
називається невизначеним інтегралом і позначається символом ![]() тобто
тобто ![]() де
де ![]() — одна з первісних функцій
— одна з первісних функцій ![]() а
а ![]() — деяка стала
— деяка стала
Правила інтегрування
![]() де
де ![]() — стала
— стала
![]()
![]()
Площа криволінійної трапеції
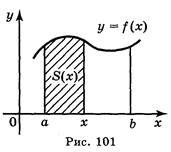 Вияснимо, як можна обчислити площу S криволінійної трапеції за допомогою первісної функції у = f(x).
Вияснимо, як можна обчислити площу S криволінійної трапеції за допомогою первісної функції у = f(x).
Позначимо
S(x) площу криволінійної трапеції з основою [а;х] (рис. 101), де х — будь-яка точка відрізку [а; х]. При х = а відрізок [а; х] перетворюється в точку і тому S(a)·= 0; при х = b маємоS(b) = S— площу криволінійної трапеції.
Доведемо, щоS(x) є первісною функціїf(x), тобтоS'(x) =f(x).
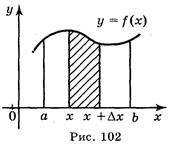
Розглянемо різницю S(x+![]() x) – S(x),
x) – S(x), ![]() х > 0 (випадок
х > 0 (випадок ![]() х < 0 розглядається аналогічно). Ця різниця дорівнює площі криволінійної трапеції з основою [x; x +
х < 0 розглядається аналогічно). Ця різниця дорівнює площі криволінійної трапеції з основою [x; x + ![]() х] (рис. 102).
х] (рис. 102).
Якщо Δx мале число, то площа приблизно дорівнюєf(x)·![]() х, тобто S(x + Δx) – S(x)
х, тобто S(x + Δx) – S(x) ![]() f(x)·Δx.
f(x)·Δx.
Таким чином, ![]()
![]() f(x).
f(x).
Якщо Δx→0, то ліва частина наближеної рівності за означенням похідної наближається доS'(x), тому
![]() , S'(x) = f(x).
, S'(x) = f(x).
Це і означає, що S(x) є первісною функції f(x).
Будь-яка первіснаF(x) відрізняється відS(x) на стале число, тобто
F(x) = S(x) + С. (1)
Із цієї рівності приx = а одержуємоF(a) =S(a) + С. ОскількиS(a) = 0, то С =F(b) і рівність (1) можна записати так:
S(x) = F(x) -F(a).
Звідси приx = b одержуємо:
 S(b) =F(b) - F(a}, S = F(b) - F(a).
S(b) =F(b) - F(a}, S = F(b) - F(a).
Отже,площу криволінійної трапеції можна обчислити за формулою S = F(b) --F(a), де F(x) — будь-яка первісна функція f(x).
Площу криволінійної трапеції можна обчислити за формулою S = F(b) -F(a), де F(x) — будь-яка первісна функція f(x).
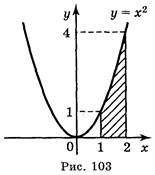
Приклад Знайдіть площу криволінійної трапеції, обмеженої лініями f(x) =x2, x = 1, x = 2, у = 0.
Розв'язання
Однією з первісних для функції f(x) =х2 є F(x) = ![]() .
.
Отже, S = F(2) - F(1) = ![]()
![]()
Таблиця первісних

Визначений інтеграл
Нехай задано неперервну функцію f(x), визначену на проміжку [a; b], тоді визначеним інтегралом від а до b функції f(x) називають приріст первісної F(x) цієї функції, тобто ![]() . Числа а і b називають відповідно нижньою і верхньою межами інтегрування.
. Числа а і b називають відповідно нижньою і верхньою межами інтегрування.
Основні правила обчислення визначеного інтеграла
Розглянемо площу фігур зверху обмежену графіком функцій у = /(х), знизу - графіком функції у = f(х) та вертикальними прямими х = а і х = b, причому функції у = f(x) і у = g(х) - неперервні на [а;b] і для всіх значень х ![]() [а;b] виконується нерівність f(x) ≥ g(x) Тоді площу S такої плоскої фігури можна знайти за формулою:
[а;b] виконується нерівність f(x) ≥ g(x) Тоді площу S такої плоскої фігури можна знайти за формулою:
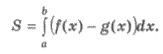
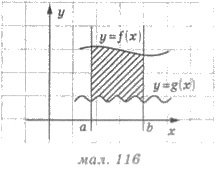
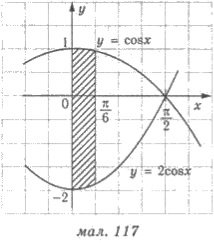
Приклад 1. Знайдіть площу фігур, обмежену графіками функцій у = соs х, у = -2 соs х та прямими x = 0 i x= π/6.
Розв’язання (мал. 117). Маємо
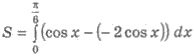
Підінтегральний вираз можна спростити. Отримаємо
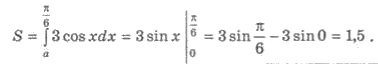
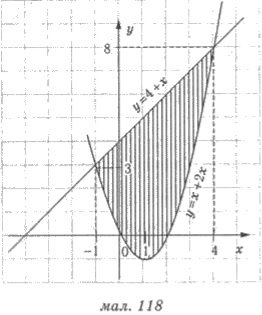
Приклад 2. Знайдіть площу фігури, обмежену графіками функцій у = х2 - 2х і у = 4х + х.
Розв’язання. Знайдемо абсциси точок перетину графіків функцій: х2 - 2х = 4 + х; х2 - 3х - 4 = 0; x1 = -1; x2 = 4.
Ординати точок перетину y1 = 3; у2 = 8. Зображуємо графіки функцій схематично (мал. 118).
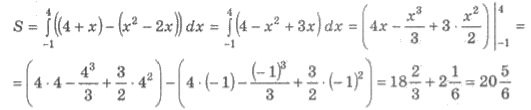
Використані джерела:
А.Г. Мерзляк,
Д.А. Номіровський,
В.Б. Полонський,
М.С. Якір,
Підручник алгебра 11 клас, 2011р. Харків «Гімназія»
Є.П. Нелін,
О.М. Роганін,
С.М. Ільїна,
ЗНО 2011 Математика Комплексна підготовка.


про публікацію авторської розробки
Додати розробку