Алгебра та початки аналізу 11 клас

ТЕМА: Первісна та її властивості

МЕТА:                                                                                                 

Формування поняття первісної функції та поняття невизначеного інтегралу,

знання таблиці первісних;                                     

 Відпрацювати таблицю первісних, правила знаходження первісних;  перевірити рівень знань з теми;  повторити формули тригонометрії, степінь з цілим показником;  готувати учнів до незалежного зовнішнього оцінювання;

розвивати логічне мислення, вміння чітко висловлювати думки, грамотно використовувати математичні терміни; виховувати почуття відповідальності, самоповаги, взаємоповаги.

1.Сприймання і усвідомлення поняття первісної. Перегляд відеоуроку.

Операції в математиці                                                                                         

Кожна дія (операція) в математиці має обернену: додавання-віднімання; множення-ділення; піднесення до степеня – добування кореня; логарифмування – потенціювання; множення одночлена на многочлен - розкладання многочлена на множники способом винесення спільного множника за дужки. 

Основна операція диференціального числення є знаходження похідної даної

функції .                                                                   Обернена операція до

диференціювання є: за відомою похідною деякої функції знайти (відновити) саму функцію , яку називають первісною F для відомої функції .                                       

Операція знаходження первісної F для даної функції називається інтегруванням.                                                                                          

Отже, інтегрування є оберненою операцією до операції диференціювання. Первісна Означення. Первісною для даної функції y=f(x) на заданому проміжку [a; b] називається така функція F(x), похідна якої для всіх x з інтервалу [a; b] дорівнює f(x), тобто Fʹ(x)=f(x) для всіх x є [a; b]. 

У фізиці трапляються задачі: відомо прискорення, треба знайти закон руху.  

При вивченні теми «Похідна» ми розв'язували задачу про знаходження швидкості прямолінійного руху по заданому закону зміни координати s(t) матеріальної точки. Миттєва швидкість v(t) дорівнює похідній функції s(t), тобто v(t) = s'(t).

У практиці зустрічається обернена задача: по заданій швидкості v(t) руху точки знайти пройдений нею шлях s(t), тобто знайти таку функцію s(i), похідна якої дорівнює v(t). Функцію s(t) таку, що s'(t) = v(t), називають первісною

gt²

функції v(t). Наприклад, якщо v{t) = gt, то s(t) =     є первісною функції v(t), 2

оскільки g'(t)  _ gt2² _^I  g 2^ 2^t  gt  v(t) .

_

Ще М. Ломоносов зазначив: «Фізик сліпий без математики», – тож на допомогу приходять знання математики: необхідність інтегрування функції.

2.Сприймання і усвідомлення основної властивості первісної, поняття невизначеного інтеграла.

Розглянемо функцію f(x) = х². Доведемо, що функції F₁(x) _ ^x3 , F₂(x) _ ^x3 2,

3    3 x3

F₃(x)  5 є первісними функції f(х).

3

                                        I              x3 I       3x2           2                           I              x3         I          2                  2

Дійсно, F₁ (x) _ 3 _  3  x  f (x), F₂ (x) _ 3 2_  x 0  x  f (x) ,

_

                  ^I              x3        I          ^{2                  2}

F₃ (x) _ 3 5_  x 0  x  f (x) .

_ x3

Взагалі будь-яка функція F(x)  + С, де С — постійна, є первісною 3

функції х². Це випливає з того, що похідна постійної дорівнює нулю.

Цей приклад свідчить, що для заданої функції первісна визначається неоднозначне.

Теорема 1. Нехай функція F(x) є первісною для f(х) на деякому проміжку. Тоді для довільної постійної С функція F(x) + С також є первісною для функції f(х).

Доведення

Оскільки F(x) — первісна функції f(x), то F'(x) = f(x). 

Тоді (F(x) + С)' = F'(x) + С' = f(х) + 0 = f(x), а ця рівність означає, що     F(x) + С є первісною для функції f(х).

Теорема 2. Нехай функція F(x) є первісною для f(x) на деякому проміжку. Тоді будь-яка первісна для функції f(x) на цьому проміжку може бути записана у вигляді F(x) + С, де С — деяка стала (число).

Доведення 

Нехай F(x) і F₁(x) — дві первісні однієї і тієї самої функції f(x), тобто F ^I (x) = f(x), F₁^I (x) = f(x). Похідна різниці g(x) = F(x) – F₁(x) дорівнює нулю, оскільки     g'(x) = F₁^I (x) - F'(x) = f(x) - f(x) = 0. Якщо g'(x) = 0 на деякому проміжку, то дотична до графіка функції у = g(x) у кожній точці цього проміжку паралельна осі ОХ. Тому графіком функції у = g(x) є пряма, яка паралельна осі ОХ, тобто g(x) = С, де С — деяка стала. Із рівностей g(x) = С, g(x) = F₁(x) - F(x) випливає, що F₁(x) – F(x) = С, або F₁(x) = F(x) + С. Теореми 1 і 2 виражають основну властивість первісної.

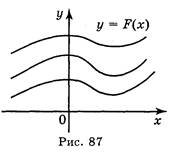
Основній властивості первісної можна надати геометричного змісту:

графіки будь-яких двох первісних для функції f одержуються один із одного паралельним перенесенням вздовж осі ΟΥ (рис. 87)

Нехай функція f має на деякому проміжку первісну. Сукупність усіх первісних для функції f(x) на проміжку називають невизначеним інтегралом цієї функції і позначають  f (x)dx . функцію f(x) називають підінтегральною функцією.

З доведених теорем випливає, що   f (x)dx = F{x) + С, де F(x) — яканебудь первісна для функції f(x) на даному проміжку, С — довільна стала (її називають сталою інтегрування). Наприклад, функція sin x є первісною для функції cos x на проміжку (-_; +), тому можна записати, що 

cosxdxsinxC .

3. Сприймання і усвідомлення таблиці первісних (таблиці невизначених інтегралів).

Користуючись таблицею похідних, можна скласти таблицю первісних

(таблицю невизначених інтегралів) для функцій, похідні яких відомі

Правило 1 знаходження первісних

•    Якщо F(x) і G(x) — первісні відповідно функцій f(x) і g(x) на деякому проміжку, то функція F(x) ± G(x) є первісною функції f(x) ± g(x).

•    Доведення: Оскільки F'(x)=f(x), G'(x)=g(x), то (F(x)± G(x))'=F'(x)± G(x)=f(x)± g(x).

•    Це правило можна сформулювати в іншій формі: інтеграл суми (різниці) функцій дорівнює сумі (різниці) інтегралів:

( f (x) g(x))dx  f (x)dxg(x)dx

Правило 2 знаходження первісних

.

•    Якщо F(x) є первісною для функції f(x), a C — стала, то CF(x) — первісна для функції Cf(x).

•    Доведення:  Оскільки F'(x )= f(x) то (CF(x))' = CF'(x) = Cf(x).

•    Це правило можна сформулювати в іншій формі: постійний множник можна виносити за знак інтеграла .

Сf (x)dx  C f (x)dx

•    Якщо F(x) є первісною для f(x), a k і b — постійні числа, причому k 0, то 1/к *F(kx +b) є первісною для функції f(kx + b).

•    Дійсно, за правилом похідної складеної функції

          маємо:                   1 F(kxb)I 

                                                  k                          

1

•    =      F'(kx +b)·k= F'(kx +b)= f(kx + b). k

•    Це правило можна записати в інтегральній формі:       1

 f (kxb)dx  k F(kxb)C

2

Розв'язання

Оскільки первісною для функції х⁵ є функція ^х6 , то згідно з правилом 3 шукані первісні: ⁶

F(x)_1 (83x)⁶ _C_(83x)⁶ _C

                                   3          6                                  18

б) Оскільки однією із первісних для функції е^х є функція е^х, то згідно з правилом 3 маємо:

F(x) = ¹₉e^9х-l + C.

2.Знайти первісні для функцій: 1) y  x⁷;

2)      y3x1⁷;

3)      f (x)  6x² 3x1;

                             3      4

4)      f (x)  ₅  ₃ 2; x       x

5)      ysin^_3x^_;

                                3 

6)      y  sin² xcos² x;

²                               x      ² x

7)      y  cos sin ;

²                               2

2

8)      f (x) .

cos2 x 1

                                        4     

4.Розв’язування прикланих задач фізичного змісту.

План розв’язування

1)    записати       математичну        залежність між    фізичними величинами;

2)    знайти первісні, використовуючи правила знаходження;

3)    використати початкові умови для знаходження конкретного вигляду первісних;

4)    записати рівняння зі знайденим значенням С.

Необхідно пригадати з курсу фізики залежності av ^' ,vs ^' . Яка з даних величин є первісною?

Швидкість руху точки задається рівнянням v 7t² 1 (м/с). Знайти рівняння руху S  S(t), якщо S(2) 12 (м).

Розв’язання

1)    v  s ^' ,

2)    S(t)  ⁷ t³ t C ,

3

3)    S(2)  ⁷2³ 2C12C4 ,

3

4)    S(t)  ⁷t³ t 4 .

3

7 ³ Відповідь: S(t)  t t 4 .

3

За аналогічною схемою розв’язати вправу №7 підручника 1, ст.375.

5. Формування умінь учнів знаходити первісні для функцій, користуючись правилами знаходження первісних. Виконання тестування.

6.Підведення підсумків уроку.

7.Домашнє завдання.

Параграф 8. Вправи № 8.6, 8.10, 8.12, 8.14.