Множення многочленів

Тема: Множення многочленів.

Мета: сформувати в учнів знання алгоритму множення  многочленів; виробити вміння перетворювати добуток двох многочленів у многочлен стандартного вигляду за названим алгоритмом; розвивати творчі й інтелектуальні здібності учнів; виховати уважність і відповідальність.

Тип уроку: засвоєння нових знань.

Обладнання: конспект уроку, кольорова крейда, підручник  алгебра 7 клас, А.Г. Мерзляк, плакат «Множення двох многочленів».

Епіграф: «Все що я пізнаю, я знаю, навіщо це мені потрібно, де і як я можу ці знання застосувати».

Хід уроку

І. Організаційний момент

(Заходжу до класу). Добрий день діти! Сідайте. (Перевіряю стан дошки, наявність вологої ганчірки, крейди, відмічаю відсутніх).

ІІ. Перевірка домашнього завдання

Хто не виконав домашнє завдання? Які  виникли питання ?

Дуже добре, тоді якщо питань нема, то здаємо зошити.

ІІІ. Актуалізація опорних знань

Перш ніж почати нашу роботу давайте з вами пригадаємо попередній матеріал.

1.       Що таке многочлен? (Сума кількох одночленів).
2.       Що є многочленом стандартного вигляду? (Многочлен, що є сумою одночленів стандартного вигляду, серед яких немає подібних членів)
3.       Що називається степенем многочлена стандартного вигляду? (Найбільший серед степенів одночленів, що до нього входять).

Молодці! Ви готові до уроку.

ІV. Мотивація навчальної діяльності. Постановка завдань, мети уроку

Рівень розвитку науки визначається ступенем її математизації. В житті не існує жодної сфери, де не застосовувалася б математика. Математичні розрахунки, формули, методи  потрібні  багатьом наукам: фізиці, хімії, географії, біології, економіці. Сьогодні на уроці ми розширимо математичні знання, які знадобляться вам у житті. Тому епіграфом до нашого уроку буде такий вислів «Все що я пізнаю, я знаю, навіщо це мені потрібно, де і як я можу ці знання застосувати».

Тема сьогоднішнього уроку «Множення многочленів».

На уроці ви повинні усвідомити правило множення многочленів та навчитись його використовувати.

При вивченні нового матеріалу будемо складати опорний конспект і записувати його у зошит.

V. Вивчення нового матеріалу

Означення. Щоб помножити одночлен на многочлен, треба помножити цей одночлен на кожен член многочлена і отримані добутки додати.

При множенні одночлена на многочлен отримуємо многочлен! 

Розглянемо з вами алгоритм множення одночлена на многочлен і запишемо його у зошит.

Виконаємо з вами приклади використовуючи даний алгоритм.

 а)7⋅ (4a⁵+2ab)=7⋅ 4a⁵+7⋅ 2ab=28a⁵+14ab;

 б)(5xy−3x²)⋅ x²=5xy⋅ x²−3x²⋅ x²=5x¹⁺²y−3x²⁺²=5x³y−3x⁴.

Молодці! З множенням многочлена на одночлен впоралися. Перейдемо з вами до множення многочлена на многочлен.

Нехай дано помножити  многочлен а + b – с на многочлен m - n, що можна записати так: (а + b – с) · (m - n).

Розглядаючи множник (m - n) як одне число (як одночлен), застосуємо правило множення многочлена на одночлен:

(а + b – с) · (m – n) = а·(m – n) + b·(m – n) + с·(m – n).

Кожний член отриманого многочлена являє собою добуток многочлена на одночлен. Застосовуючи знову попереднє правило, отримаємо:

(a·m – a·n) + (b·m – b·n) + (c·m – с·n).

Розкриваємо дужки (по принципу додавання та віднімання многочленів):

(а + b – с) (m – n) = а·m – а·n + b·m – b·n – c·m + с·n. 

Отже, правило:

Щоб помножити многочлен на многочлен, потрібно кожний член першого многочлена помножити на кожний член другого многочлена і отримані добутки додати.

Наприклад, (а-2)(3а+4)=а•3а+4а-2•3а-2•4=3а²+4а-6а-8=3а²-2а-8.

При множенні многочленів потрібно пам'ятати правила знаків, а саме:

(+х)•(+у)=ху;

(-х)•(-у)=ху;

(-х)•(+у)=-ху;

(+х)•(-у)=-ху.

VІ.  Застосування знань

А зараз перейдемо до розв’язування вправ. Записуємо:

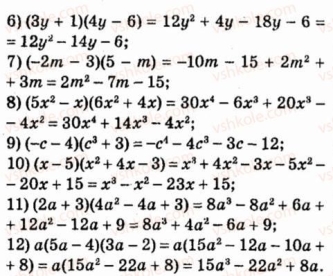
VІІ. Підбиття підсумків. Оцінювання учнів

Отже, ми з вами розглянули нову тему, а зараз дайте відповідь на наступні запитання.

1. Що ми робили на уроці?
2. Що нового дізнались на уроці?
3. Як перемножити многочлени?
4. Що сподобалось на уроці? Що не сподобалось?

VІІІ. Домашнє завдання 

Опрацювати §2 п. 10, 11. Розв’язати №356, 358, 393.