Підготовка до ЗНО та НМТ (геометрія)
Підготовка до ЗНО та НМТ (геометрія)
Пропонується низка завдань для повторення окремих розділів геометрії
Завдання 1. Сторони прямокутника дорівнюють 5 см і 12 см.
1) Обчисліть радіус описаного кола.
Відповідь: 6,5 см
Розв’язання. Діагональ прямокутника дорівнює 13 см (за теоремою Піфагора) і є діаметром описаного кола, отже, ![]() . Отже,
. Отже, ![]() см.
см.
2) Обчисліть діаметр кола, вписаного в один із прямокутних трикутників, який утворено діагоналлю прямокутника.
Відповідь: 4 см.
Розв’язання. Нехай ![]() - радіус вписаного кола; знаходимо за формулою
- радіус вписаного кола; знаходимо за формулою ![]() , де
, де
![]() – катети трикутника,
– катети трикутника, ![]() – гіпотенуза; отже,
– гіпотенуза; отже, ![]() і діаметр 4 см.
і діаметр 4 см.
Завдання 2. Установіть відповідності між початком речення (1 – 4) та його закінченням
(А – Д).
-
Периметр ромба з гострим кутом
 , в який вписано коло А 20 см
, в який вписано коло А 20 см
довжиною ![]() , дорівнює…
, дорівнює…
- Гіпотенуза прямокутного рівнобедреного трикутника з площею Б 16 см
100 см2 дорівнює…
- Радіус кола, вписаного у квадрат з площею 400 см2, дорівнює… В 40 см
- Висота рівнобічної трапеції з перпендикулярними діагоналями Г 12 см
і площею 256 см2 дорівнює…
Д 10 см
|
|
А |
Б |
В |
Г |
Д |
|
1 |
|
|
Х |
|
|
|
2 |
Х |
|
|
|
|
|
3 |
|
|
|
|
Х |
|
4 |
|
Х |
|
|
|
Відповідь:
Розв’язання.
1) Висота ![]() цього ромба дорівнює діаметру вписаного кола
цього ромба дорівнює діаметру вписаного кола ![]() , тому за формулою
, тому за формулою ![]() маємо:
маємо: ![]() і
і ![]() ; сторону ромба знаходимо за формулою
; сторону ромба знаходимо за формулою ![]() см; отже, периметр ромба
см; отже, периметр ромба ![]() см.
см.
2) Площу прямокутного рівнобедреного трикутника з катетом ![]() знаходимо за фор-мулою
знаходимо за фор-мулою ![]() ,
, ![]() ,
, ![]() ; гіпотенуза
; гіпотенуза ![]() см.
см.
3) Радіус кола, вписаного у квадрат, дорівнює ![]() , де а – сторона квадрата. За умовою
, де а – сторона квадрата. За умовою
площа квадрата 400 см2, тому ![]() см і радіус дорівнює 10 см.
см і радіус дорівнює 10 см.
4)
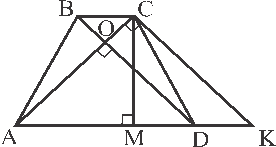
Нехай ABCD - задана трапеція, СМ![]() АD,
АD, ![]() ; побудуємо СК׀׀BD, тоді трикутники ABC, DCB, CDK - рівні і площа трапеції ABCD дорівнює площі трикутника АСК;
; побудуємо СК׀׀BD, тоді трикутники ABC, DCB, CDK - рівні і площа трапеції ABCD дорівнює площі трикутника АСК; ![]() ,
, ![]() , тому
, тому ![]() і
і ![]() ; нехай
; нехай ![]() ;
; ![]() ; отже,
; отже, ![]() см.
см.
Завдання 3. У трикутнику АВС: ![]() ,
, ![]() . Пряма СМ перпендикулярна до АС і
. Пряма СМ перпендикулярна до АС і
точка М розташована на стороні АВ цього трикутника. Знайдіть відношення довжин
відрізків АМ та ВС.
Відповідь: 2
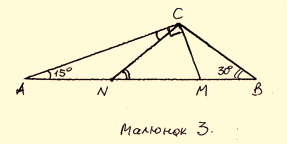
Розв’язання. Нехай CN – медіана прямокутного трикутника АСМ (малюнок 3); за властивістю медіани ![]() , отже
, отже ![]() і
і ![]() . Для ∆АСN кут СNМє зовнішнім, він дорівнює сумі внутрішніх, не суміжних з ним, тобто
. Для ∆АСN кут СNМє зовнішнім, він дорівнює сумі внутрішніх, не суміжних з ним, тобто ![]() . Тоді ∆СNВ є рівнобедреним, СВ =СN. Зазначимо, що
. Тоді ∆СNВ є рівнобедреним, СВ =СN. Зазначимо, що ![]() , отже,
, отже,
АМ = ![]() і
і ![]() .
.
Завдання 4. Площа бічної поверхні конуса ![]()
![]() , радіус основи – 6 см.
, радіус основи – 6 см.
1) Знайдіть кут при вершині осьового перерізу цього конуса.
Відповідь: ![]()
Розв’язання. Площу бічної поверхні конуса обчислюємо за формулою ![]() , де R – радіус основи, l – твірна; отже,
, де R – радіус основи, l – твірна; отже, ![]() ,
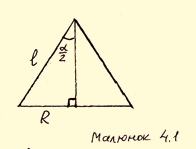
, ![]() см. Осьовий переріз конуса (малюнок 4.1) – рівнобедрений трикутник, тому висота конуса – медіана та бісектриса цього трикутника. Нехай α – шуканий кут, тоді
см. Осьовий переріз конуса (малюнок 4.1) – рівнобедрений трикутник, тому висота конуса – медіана та бісектриса цього трикутника. Нехай α – шуканий кут, тоді ![]() .
.
2) Знайдіть відношення площі бічної поверхні конуса до площі поверхні кулі, вписаної у цей конус.
Відповідь: 1,5
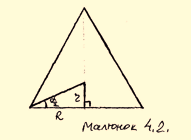
Розв’язання. Осьовий переріз конуса – рівнобедрений трикутник із кутом при вершині ![]() , отже, цей трикутник – рівносторонній, і радіус кола, вписаного в нього, є радіус кулі, вписаної в конус (малюнок 4.2). Цей радіус – r, знаходимо за формулою:
, отже, цей трикутник – рівносторонній, і радіус кола, вписаного в нього, є радіус кулі, вписаної в конус (малюнок 4.2). Цей радіус – r, знаходимо за формулою: ![]()
![]() . Площа поверхні кулі дорівнює
. Площа поверхні кулі дорівнює ![]() ,
,
отже, ![]()
![]() . Знаходимо відношення площі бічної поверхні конуса до площі поверхні кулі, вписаної у цей конус:
. Знаходимо відношення площі бічної поверхні конуса до площі поверхні кулі, вписаної у цей конус: ![]() .
.
Завдання 5. У кубі ребро дорівнює ![]() см. Знайдіть відстань між мимобіжними діагоналями двох суміжних граней.
см. Знайдіть відстань між мимобіжними діагоналями двох суміжних граней.
Відповідь: 12 см
Розв’язання. Нехай ![]() - куб, ребро якого дорівнює а,
- куб, ребро якого дорівнює а, ![]() см . Діагоналі
см . Діагоналі![]() та
та ![]() - мимобіжні діагоналі двох суміжних граней.
- мимобіжні діагоналі двох суміжних граней.
Застосуємо теорему про відстань між мимобіжними прямими: якщо одна з даних прямих а перпендикулярна до деякої площини α та перетинає її в точці А, а інша пряма - b має проекцію на площину α - пряму ![]() , тоді відстань між прямими а і b дорівнює відстані між точкою А та прямою
, тоді відстань між прямими а і b дорівнює відстані між точкою А та прямою ![]() (малюнок 5.1).
(малюнок 5.1).
Для даної задачі: пряма ![]() (а) перпендикулярна до площини
(а) перпендикулярна до площини ![]() (α) і перетинає її в точці
(α) і перетинає її в точці ![]() , проекцією діагоналі
, проекцією діагоналі ![]() ( b) на площину
( b) на площину ![]() ( α) є відрізок
( α) є відрізок ![]() (
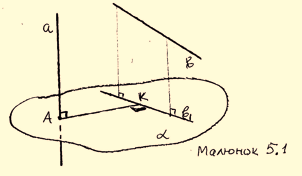
(![]() ) (малюнок 5.2). Розглянемо переріз
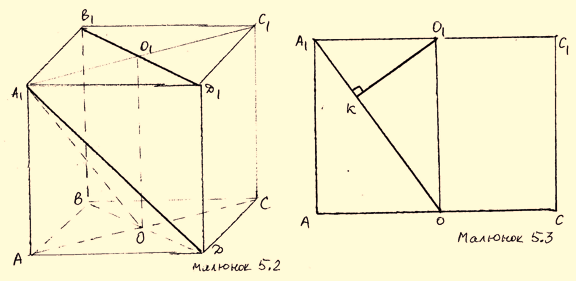
) (малюнок 5.2). Розглянемо переріз ![]() і в ньому прямокутний трикутник
і в ньому прямокутний трикутник ![]() (малюнок 5.3): нехай
(малюнок 5.3): нехай ![]() , тоді
, тоді ![]() - шукана відстань між
- шукана відстань між ![]() та
та ![]() ;
; 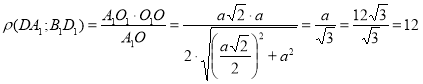 .
.


про публікацію авторської розробки
Додати розробку
