Підготовка до ЗНО з теми" Цілі вирази"
Завдання на тему «Цілі вирази»
Одночлени
ЗНО 2016

Многочлени
ЗНО 2015

Пробне ЗНО 2019

Множення многочлена на одночлен
ЗНО 2015

ЗНО 2019

Формули скороченого множення
1. Подайте у вигляді многочлена вираз:
а) (а – 4)(а + 4)
б) (0,2х – 5у)( 0,2х + 5у)
в) (– х –![]() )( х –
)( х –![]() ) =
) =
г) (b + 2) (b – 2)
д) (а2 – 1) (а2 + 1)
е) (0,3с + 2d)(–2d +0,3с)
2) Спростіть вираз
а) (у – 4) (у + 4) – (у + 2)2
б) (х – 2)2 + (3 – х) (3 + х)
Пробне ЗНО 2017

ЗНО 2018

Розкладання многочлена на множники
Пробне ЗНО 2017

ЗНО 2018

Завдання зі збірника «Сучасна підготовка до ЗНО 2021»
16. Спростити вираз: а) – (9х – 4) + 3(1 + 3х)
б) – (6х + 7) + 2(3х + 8)
17. Запишіть у вигляді многочлена: а) (2с – 1)(4с + 1)
б) (1– 3с)(с + 4)
18. Запишіть у вигляді многочлена: а) аb3(а – 2b); б) (3а + b) а3b
23. Спростіть вираз: а) (а – 3)2 + 6а – 9;
б) (а + 4)2 – 8а – а2
24. Розкладіть на множники: а) 36m2 – 1;
б) 1– 25m2
25. Подайте у вигляді квадрата двочлена: а) 9х 2 + 6х + 1;
б) 4х 2 – 8х + 4
26. Спростіть вираз: а) ![]() ; б)
; б) ![]()
27. Спростіть вираз: а) ![]() ; б)
; б) ![]()
ЗНО 2006
Завдання 3
Знайдіть вираз, тотожно рівний виразу х4 + х3 – х - 1
|
А |
Б |
В |
Г |
Д |
|
(х+1)2(х2+х+1) |
(х2-х+1) (х-1)2 |
(х-1)3(х+1) |
(х-1) (х+1)3 |
(х2-1) (х2+х+1) |
ЗНО 2008
Завдання 12
Знайдіть значення виразу х2 – 4 х – 1, якщо х = 2 – ![]()
|
А |
Б |
В |
Г |
Д |
|
- 5 |
5 |
13 – 4 |
13 + 4 |
Інша відповідь |
ЗНО 2009
Завдання 1
Спростіть вираз ![]() .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
– |
|
ЗНО 2010
Завдання 29
Знайдіть значення виразу ![]() ∙
∙![]() –
– ![]() , якщо m = 4,25
, якщо m = 4,25
ЗНО 2011
28. Установіть відповідність між виразами (1 – 4) та їхніми значеннями, якщо х = 0,5
(А – Д )
Вираз Значення виразу
1 ![]() А 1,5
А 1,5
2 ![]() ∙
∙![]() Б 2,5
Б 2,5
3 ![]() В – 0,25
В – 0,25
4 (х – 5)2 + 5(2х - 5) Г – 2,5
Д 0,25
ЗНО 2012(осн. сесія 2)
21. До кожного виразу (1-4) доберіть тотожно рівний йому вираз(А – Д)
1 (а – 8) (а + 8) А а2 – 16а + 64
2 (а – 8)2 Б а2 – 64
3 (а – 4)( а2 + 4а + 16) В а2 – 20а + 64
4 (а – 4)(а – 16) Г а3 + 64
Д а3 – 64
ЗНО 2012(додаткова сесія )
25. Спростіть вираз 2(а2 – 5ab + 4b2) – 3(2а2 – 2ab + 3b2) та обчисліть його значення, якщо
а =1,1; b = 0,8.
ЗНО 2013(сесія 1)
2. Укажіть вираз, тотожно рівний виразу (2х + 5)(3 – х)
|
А |
Б |
В |
Г |
Д |
|
15 + х – 2х2 |
15 + х + 2х2 |
15 + 6х – 2х2 |
15 + 11х – 2х2 |
15 + 11х + 2х2 |
ЗНО 2016
7. Спростіть вираз ![]() -
- ![]()
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
0 |
ЗНО 2017

ЗНО 2018
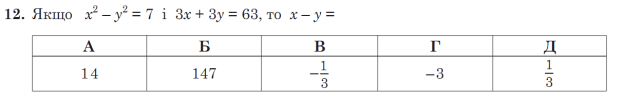
ЗНО 2020 основна
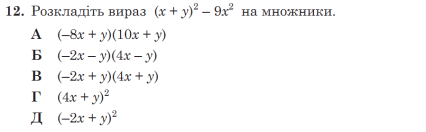
(x +y -3x)(x + y +3x) = (- 2x + y)(4x + y) – В
2020 додаткове

х + 2х – 4 = 3х – 4 – А

ЗНО 2021

Демонстраційне ЗНО 2021
7.

1
Підготовка до ЗНО
Тема: Цілі вирази.
1. Вирази зі змінними. Тотожні вирази.
Раціональні вирази a + b = b + a (a ![]() b) = a
b) = a ![]() b
b
![]()
![]() ab = ba - (a
ab = ba - (a ![]() b) = a
b) = a ![]() b Числові Зі змінними | (a
b Числові Зі змінними | (a ![]() b)c = ac
b)c = ac ![]() bc a + a = 2a
bc a + a = 2a
![]()
![]()
![]()
![]() a(b
a(b![]() c ) = ab
c ) = ab![]() ac a ∙ a = a2
ac a ∙ a = a2
цілі дробові цілі дробово - раціональні
Цілий вираз: ![]() – не містить зміну в знаменнику
– не містить зміну в знаменнику
Дробово – раціональні: ![]() .
.
Цілі вирази поділяються на одночлени і многочлени.
2. Одночлени
Одночлени – це добуток чисел, букв та їх степенів
![]()
![]() 5х2у
5х2у
коефіцієнт буквена частина
(степінь одночлена – це сума показників змінних, що входять до їх складу
n = 2 +1 =3 - степінь). 5х2у – одночлен третього степеня.
Дії з одночленами
5х2у і ![]() х2у – подібні
х2у – подібні
5х2у + ![]() х2у = 5,2х2у = х2у – додавання
х2у = 5,2х2у = х2у – додавання
5х2у ∙ ![]() х2у = х4у2 – множення
х2у = х4у2 – множення
(5х2у)2 = 25 х4у2– піднесення до степеня
ЗНО 2016

Одночлен множимо два одночлена: спочатку коефіцієнти, а потім множимо буквені частини: 2х5 ![]() В
В
3. Многочлени
Р(х) = ахn + bxn-1+… + c(n – степінь)
Многочлени – це сума декількох одночленів. Степінь многочлена – це найвищий показник степеня одночлена який входить до його складу
ах + b – лінійний двочлен (5х + 3) – вираз першого степеня
(лінійний – х в першому степені, а двочлен – два доданки)
ах2 + bх + с – квадратний тричлен (2х2 - 5х + 2) – це многочлен другого степеня – найвищий степінь – квадрат, тричлен – три доданки.
Дії з многочленами
4. Додавання і віднімання многочленів
3х + 2 та 2х – 3
(3х + 2) + (2х – 3)= 3х + 2+2х – 3 = 5х -1
(3х + 2) - (2х – 3)= 3х + 2-2х +3 = х +5
5. Множення многочлена на одночлен
(a ![]() b)c = ac
b)c = ac ![]() bc
bc
ЗНО 2015

Розкриємо дужки: 10х + 12 ![]() А
А
Пробне ЗНО 2019

Можна розкрити дужки. Але в завдані сказано «обчислити значення виразу», то краще просто підставити.
3(а –1) = 3(0,7 – 1) = 3∙(– 0,3) = – 0,9![]() А
А
6. Множення многочлена
(a + b)(b + d) = ас + ad + bc + bd
7. Формули скороченого множення
Квадрат двочлена
(a + b)2 = а2 +2аb + b2 – квадрат суми
(a – b)2 = а2 –2аb + b2 – квадрат різниці
1. Подайте у вигляді многочлена вираз:
а) (а – 4)(а + 4) = а2 – 42 = а2 – 16
б) (0,2х – 5у)( 0,2х + 5у) = (0,2х)2 – (5у)2 = 0,04х2 – 25у2
в) (– х –![]() )( х –
)( х –![]() ) = – ( х +
) = – ( х +![]() )( х –
)( х –![]() ) = – (х2 – (
) = – (х2 – (![]() )2 ) = – (х2 –
)2 ) = – (х2 – ![]() ) = – х2 +
) = – х2 + ![]()
г) (b + 2) (b – 2) = b2 – 22 = b2 – 4
д) (а2 – 1) (а2 + 1) = (а2)2 – 12 = а4 – 1
е) (0,3с + 2d)(–2d +0,3с) = (0,3с – 2d) (0,3с + 2d) = (0,3с)2 – (2d)2 = 0.09c2 – 4 d2
2) Спростіть вираз
а) (у – 4) (у + 4) – (у + 2)2 = у2 – 16 – (у2 + 4 у + 4) = у2 – 16 – у2 – 4у – 4 =
= – 4у – 20
б) (х – 2)2 + (3 – х) (3 + х) = х2 – 4х + 4 + 9 – х2 = – 4х + 13 = 13 – 4х
Квадрат тричлена
(a + b + с)2 = а2 + b2 + с2 + 2аb + 2ас + 2bс
Різниця квадратів
a2 – b2 = (a + b) (a – b)
(a + b) (a – b) = a2 – b2
Куб суми і різниці
(a + b)3 = а3 +3а2b + 3аb2 + b3 – куб суми
(a – b)3 = а3 – 3а2b + 3аb2 – b3– куб різниці
Сума і різниця кубів
а3 + b3 = (a + b)( а2 – аb + b2) – суми кубів
а3 – b3 = (a – b) ( а2 + аb + b2) – різниця кубів
Пробне ЗНО 2017

Підставимо значення х = t – 2 в вираз х2 – t2 і застосуємо формулу скороченого множення – квадрат різниці
х2 – t2 = (t – 2)2 – t2 = t2 – 4t + 4 – t2 = – 4t + 4 = 4 – 4t![]() Б
Б
ЗНО 2018

Розкриємо дужки(множимо одночлен на многочлен) і застосуємо формулу скороченого множення – квадрат суми.
а(a + 2b) – (a + b)2 = а2 + 2аb – (а2 +2аb + b2) = а2 + 2аb – а2 – 2аb – b2 = – b2
– b2![]() В
В
Розкладання многочлена на множники
1. Винесення спільного множника за дужки
ab![]() ac = a(b
ac = a(b![]() c )
c )
a(b + c ) + d(b + c ) = (b + c ) (a + d )
2. Спосіб групування
ab + ac + db + dс = (ab + ac) + (db + dс) = а(b + c) + d(b + с) = (b + с)(a + d )
3. Використання формул скороченого множення
a2 – b2 = (a + b) (a – b)
(a ![]() b)2 = а2
b)2 = а2 ![]() 2аb + b2
2аb + b2
а3 ![]() b3 = (a
b3 = (a ![]() b)( а2
b)( а2 ![]() аb + b2)
аb + b2)
(a ![]() b)3 = а3
b)3 = а3 ![]() 3а2b + 3аb2
3а2b + 3аb2 ![]() b3
b3
4. Застосування різних способів розкладання многочлена
Пробне ЗНО 2017

Виразимо а: a + b = 6; а = 6 – b ![]() 25 – 2(6 – b) – 2b = 25 – 12 + 2b – 2b =
25 – 2(6 – b) – 2b = 25 – 12 + 2b – 2b =
= 13 ![]() Г
Г
або 25 – 2а – 2b = 25 – 2(а + b) = 25 – 2∙6 = 25 – 12 = 13 ![]() Г
Г
ЗНО 2018

Винесемо 2 за дужки і поділимо на 2. ![]() =
= ![]() = а + 1
= а + 1![]() В
В
Сканаві 2.195. Рівень Б
Спростити вираз
![]() :
: 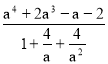 =
=
1) Розкладемо на множники вираз а4 – а2 – 2а – 1.
а4 – а2 – 2а – 1= а4 – (а2 + 2а + 1) = (а2 + 2а + 1 квадрат суми) = а4 – (а + 1)2
(даний вираз різниця квадратів a2 – b2 = (a + b) (a – b) = (а2 – (а+1)) (а2 + а + 1) = (а2 – а –1) (а2 + а + 1)
2) Розкладемо на множники вираз а3 – 2а2 + 1. Розпишемо – 2а2 = – а2 – а2, та згрупуємо вираз.
а3 – 2а2 + 1= а3 – а2 – а2 + 1 = (а3 – а2) – (а2 – 1) = а2(а –1) – (а –1)(а +1) =
= ((а –1) – спільний множник) (а –1)( а2 – (а +1)) = (а –1)( а2 – а –1).
3) Розкладемо на множники вираз а4 + 2а3 – а – 2. Згрупуємо вираз:
(а4 + 2а3) – (а + 2), винесемо спільний множник а3(а + 2) – (а + 2), ще раз винесемо спільний множник (а + 2)( а3– 1). ( а3– 1) – різниця кубів.
а3 – b3 = (a – b) ( а2 + аb + b2) – різниця кубів
(а + 2)( а3 – 1) = (а + 2)(а – 1)( а2 + а + 1)
4) 1 + ![]() +
+ ![]() =
= ![]() =
= ![]()
5) ![]() =
= ![]()
6) 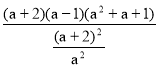 = (а + 2)(а – 1)( а2 + а + 1)∙
= (а + 2)(а – 1)( а2 + а + 1)∙![]() =
= ![]()
7) ![]() :
:![]() =
= ![]() ∙
∙![]() =
= ![]()
Завдання зі збірника «Сучасна підготовка до ЗНО 2021»
16. Спростити вираз: а) – (9х – 4) + 3(1 + 3х) = – 9х + 4 + 3 + 9х = 7
б) – (6х + 7) + 2(3х + 8)
17. Запишіть у вигляді многочлена:
а) (2с – 1)(4с + 1) = 8c2 – 4c + 2c – 1 = 8c2 – 2c – 1
б) (1– 3с)(с + 4)
18. Запишіть у вигляді многочлена: а) аb3(а – 2b) = а2b3 – 2аb4;
б) (3а + b) а3b
19. Виконайте ділення: а) ![]() :
: ![]() =
= ![]() ∙
∙ ![]() = 6; б)
= 6; б) ![]() :
: ![]()
23. Спростіть вираз:
а) (а – 3)2 + 6а – 9 = а2 – 2∙3а + 9 + 6а – 9 = а2 – 6а + 9 + 6а – 9 а = а2;
б) (а + 4)2 – 8а – а2
24. Розкладіть на множники: а) 36m2 – 1 = (6m)2 – 12 = (6m – 1) (6m + 1);
б) 1– 25m2
25. Подайте у вигляді квадрата двочлена:
а) 9х 2 + 6х + 1 = (3х)2 + 2∙3x∙1 + 1 = (3х + 1)2;
б) 4х 2 – 8х + 4.
26. Спростіть вираз: а) ![]() =
= ![]() =5; б)
=5; б) ![]()
27. Спростіть вираз: а) ![]() =
= ![]() =
= ![]() ;
;
б) ![]()
Завдання для самостійної роботи
ЗНО 2006
Завдання 3
Знайдіть вираз, тотожно рівний виразу х4 + х3 – х - 1
|
А |
Б |
В |
Г |
Д |
|
(х+1)2(х2+х+1) |
(х2-х+1) (х-1)2 |
(х-1)3(х+1) |
(х-1) (х+1)3 |
(х2-1) (х2+х+1) |
х4 + х3 – х – 1 = (х4 + х3 ) – (х + 1) = х3(х + 1) – (х + 1) = (х + 1) (х3 – 1) =
= (х + 1) (х–1)( х2 + х +1) = ( х2 – 1) ( х2 + х +1) – Д
ЗНО 2008
Завдання 12
Знайдіть значення виразу х2 – 4 х – 1, якщо х = 2 – ![]()
|
А |
Б |
В |
Г |
Д |
|
- 5 |
5 |
13 – 4 |
13 + 4 |
Інша відповідь |
х2 – 4х + 4 = (х – 2)2 = (2 – ![]() – 2) = (–
– 2) = (–![]() )2 = 5 – Б
)2 = 5 – Б
ЗНО 2009
Завдання 1
Спростіть вираз ![]() .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
– |
|
![]() =
= ![]() =
= ![]() – В
– В
ЗНО 2010
Завдання 29
Знайдіть значення виразу ![]() ∙
∙![]() –
– ![]() , якщо m = 4,25
, якщо m = 4,25

ЗНО 2011
28. Установіть відповідність між виразами (1 – 4) та їхніми значеннями, якщо х = 0,5
(А – Д )
Вираз Значення виразу
1 ![]() А 1,5
А 1,5
2 ![]() ∙
∙![]() Б 2,5
Б 2,5
3 ![]() В – 0,25
В – 0,25
4 (х – 5)2 + 5(2х - 5) Г – 2,5
Д 0,25
1. ![]() = х-3 = 0,5 – 3 = -2,5 Г
= х-3 = 0,5 – 3 = -2,5 Г
2. ![]() ∙
∙![]() =
= ![]() ∙
∙![]() =
= ![]() ∙
∙![]() =
= ![]() ∙
∙![]() =
= ![]() ∙
∙![]() =
= ![]() ∙
∙![]() =
=
= ![]() ∙
∙![]() = –
= – ![]() ∙
∙![]() = –
= –![]() = –
= –![]() = – 0,25 В
= – 0,25 В
3. ![]() =
= ![]() = х+1 = 0,5 + 1 = 1,5 А
= х+1 = 0,5 + 1 = 1,5 А
4. (х – 5)2 + 5(2х – 5) = х2 – 10х +25 + 10х – 25 = х2 = 0,52 = 0,25 Д
ЗНО 2012(осн. сесія 2)
21. До кожного виразу (1-4) доберіть тотожно рівний йому вираз(А – Д)
1 (а – 8) (а + 8) А а2 – 16а + 64
2 (а – 8)2 Б а2 – 64
3 (а – 4)( а2 + 4а + 16) В а2 – 20а + 64
4 (а – 4)(а – 16) Г а3 + 64
Д а3 – 64
1. а2 – 64 – Б 3. а3 – 43– Д
2. а2 – 16а + 64 – А 4. а2 – 16а – 4а + 64 = а2 – 20а + 64 – В
ЗНО 2012(додаткова сесія )
25. Спростіть вираз 2(а2 – 5ab + 4b2) – 3(2а2 – 2ab + 3b2) та обчисліть його значення, якщо
а =1,1; b = 0,8.
Розв’язок: 2(а2 –5аb + 4b2) – 3(2а2 –2аb + 3b2) = 2а2 –10аb + 8b2 – 6а2 +6аb – 9b2 =
= – 4а2 – 4аb – b2 = – (4а2 + 4аb + b2) – виділимо повний квадрат тричлена:
– (2а + b)2 = – (2∙1,1 + 0,8)2 = – (2,2 + 0,8)2 = – (3)2 = –9
ЗНО 2013(сесія 1)
2. Укажіть вираз, тотожно рівний виразу (2х + 5)(3 – х)
|
А |
Б |
В |
Г |
Д |
|
15 + х – 2х2 |
15 + х + 2х2 |
15 + 6х – 2х2 |
15 + 11х – 2х2 |
15 + 11х + 2х2 |
![]()
(2х + 5)(3 – х) = 2х ∙ 3 – 2х ∙ х + 5 ∙ 3 –5 ∙ х = 6х – 2х2 + 15 –5х = – 2х2 + х + 15 =
15 + х – 2х2 – А
ЗНО 2016
7. Спростіть вираз ![]() -
- ![]()
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
0 |
![]() -
- ![]() =
= ![]() =
= ![]() =
= ![]() – А
– А
ЗНО 2017

(х – 2)2 + 4х = х2 – 4х + 4 + 4х = х2 + 4 – Д
ЗНО 2018
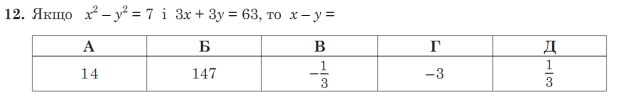
(х – у) (х + у) = 7; х – у = ![]() і 3(х + у) = 63; х + у = 63:3; х + у = 21
і 3(х + у) = 63; х + у = 63:3; х + у = 21 ![]()
х – у = ![]() =
= ![]() – Д
– Д
ЗНО 2020 основна
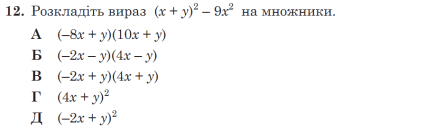
(x +y -3x)(x + y +3x) = (- 2x + y)(4x + y) – В
2020 додаткове

х + 2х – 4 = 3х – 4 – А

(2х – 3)2 + 12х = 4х2 – 12х +9 +12х = 4х2 +9 – Б
ЗНО 2021

(а – 4)2 – а2 = а2 – 8а + 16 – а2 = – 8а + 16 – А
Демонстраційне ЗНО 2021
7.

(![]() )(
)(![]() ) =
) = ![]() = 2 – а2 – Б
= 2 – а2 – Б


про публікацію авторської розробки
Додати розробку
