Підготовка учнів 5 класу до шкільного етапу олімпіади з математики

Про матеріал

Розробка розрахована для допомоги вчителям математики, які викладають у 5 класах, для підготовки учнів до шкільної олімпіади з математики. Містить цікаві завдання з різних тем, вказівки та детальні розв’язки.

Перегляд файлу

N.Sapko

Підготовка учнів 5 класу до шкільного етапу

олімпіади з математики

Задачі з розв’язками

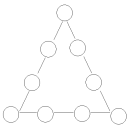Задача 1. Дано числа 1, 2, 3, 4, 5, 6, 7, 8, 9. Розташуйте їх так, щоб сума чисел на кожній стороні трикутника на рис. дорівнювала 20.

Вказівка. Можливі кілька варіантів відповіді.

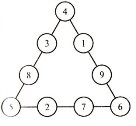$C:\Users\Наташа\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\img035.jpg$ Відповідь:

Задача 2. Наповнена доверху водою посудина важить 5 кг, а наповнена наполовину – 3 кг 250 г. Скільки води вміщає посудина? Якою є маса порожньої посудини?

Розв’язання.

Маса посудини, наповнена водою наполовину, складається:

Маса порожньої Маса води, яка наполовину

посуди + наповнює посудину = 3кг 250г

2) Маса посуди, повністю наповненої водою, складається:

Маса порожньої Маса води, яка Маса води,

наполовину яка наполовину

посуди + наповнює посудину + наповнює посудину = 5кг

3) 5 кг – 3 кг 250 г = 1 кг 750 г – маса води, що наповнює посудину наполовину;

4) 1 кг 750 г · 2 = 3 кг 500 г – маса води, що повністю наповнює посудину;

5) 5 кг – 3 кг 500 кг = 1 кг 500 г - маса порожньої посудини.

Відповідь: 3 кг 500 г; 1 кг 500 г.

Задача 3. Ілля Муромець, Добриня Микитич і Альоша Попович вступили в бій з кількома велетнями. Отримавши по 3 удари богатирськими булавами, велетні почали втікати. Найбільше ударів наніс Ілля Муромець -7, найменше всього – Альоша Попович - 3. Скільки всього було велетнів?

Розв’язання.

Кількість всіх ударів повинно бути кратне 3: 12, 15, 18.
7+3 = 10 (ударів) – нанесли І.М. і А. П.
10 : 3 = 3 (ост. 1) отже велетнів було більше, ніж 3
Припустимо, велетнів було 4, тоді ударів зробили 3х4=12
12 – 10 = 2 (удари)- міг зробити Д.М.
Припустимо, велетнів було 5, тоді ударів зробили 3х5=15
15 – 10 = 5 (ударів) міг зробити Д.М., що задовольняє умову задачі.
Припустимо, велетнів було 6, тоді ударів зробили 3х6=18
18 -10 = 8 (ударів)- міг нанести Д.М., але це суперечить умові задачі.

Відповідь: 5 велетнів.

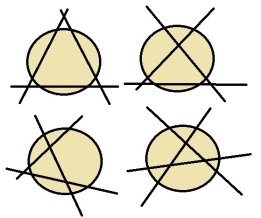Задача 4. Як розділити круглий млинчик трьома прямолінійними розрізами на 4, 5, 6, 7 частин?

Задача 5. Є 12 – літрова бочка, наповнена квасом, і дві порожні бочки — в 5 і 8 л. Спробуйте, користуючись цими бочками: а) розділити квас на дві частини — 3 і 9 л; б) розділити квас на дві рівні частини

Розв’язання. Спочатку розв’язується завдання а), і з нього вже виводиться розв’язання задачі б). Розв’язання задачі а) приведено в рядках 1–4 таблиці, а розв’язання задачі б) наведено в рядках 1–8 таблиці.

Літри/ кроки	12 л	5 л	8 л
1	12	0	0
2	4	0	8
3	4	5	3
4	9	0	3
5	9	3	0
6	1	3	8
7	1	5	6
8	6	0	6

Задача 6. Розв’язати числовий ребус «УДАР+УДАР=ДРАКА»

Розв’язання. Очевидно, що Д=1, тому А=2 або А=3, але з останнього стовпчика А- парне, тому А=2, звідки Р=6 (оскільки 1 вже задіяна), далі очевидно.

Відповідь: 8126+8126=16252

Задача 7. Андрій, Борис і Віктор- друзі. Один із них їздить до школи на автобусі, інший – на трамваї, а третій – на тролейбусі. Одного разу Андрій пішов проводжати свого друга до зупинки автобуса. Тут повз них проїхав тролейбус, і третій друг крикнув їм з вікна тролейбуса: «Борю, ти забув у школі зошита». Хто на чому їздить додому?

Розв’язання.

	Трамвай	Тролейбус	Автобус
Боря	-	-	+
Віктор	-	+	-
Андрій	+	-	-

Задача 8. Бідон місткістю 10 л заповнено молоком. Як перелити з нього 5л молока в семилітровий бідон, використовуючи порожній трилітровий бідон?

Розв’язання.

Складемо таблицю:

Бідони	Переливання
10л	3	3	6	6	9	9	2	2
7л	7	4	4	1	1	0	7	5
3л	0	3	0	3	0	1	1	3

Задача 9.

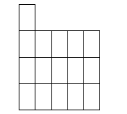Розріжте фігуру по лініях сітки на чотири одинакові, що не є прямокутниками.

Відповідь.

Можливі розв’язання наведені на рисунках.

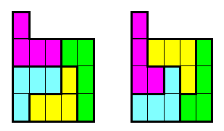
Задача 10. Розділіть зображену на рису фігуру на 4 рівні частини.

Відповідь.

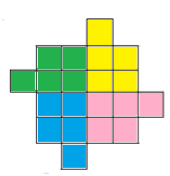
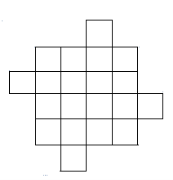
Задача 11. На рибалку Володя йшов пішки, а повертався на велосипеді. На ввесь шлях він витратив 50 хв. Іншим разом «туди» і «назад» він проїхав на велосипеді за 24 хв. За скільки хвилин Володя пройде ввесь шлях в обидва кінці пішки?

Розв’язання.

Походи на рибалку	S	t
1 раз	пішки→	50 хв	₁
1 раз	велосипедом←	50 хв	₂
2 раз	велосипедом→	24 хв	₂
2 раз	велосипедом←	24 хв	₂
3 раз	пішки→	?	₁
3 раз	пішки←	?	₁

Оскільки на ввесь шлях на велосипеді Володя витратив 24 хв, то на шлях в один бік йому потрібно: 24 :2=12 хв.
Якщо на рибалку Володя йде пішки, а повертається на велосипеді, то йому потрібно 50 хв. Але ми знаємо, що на шлях в один бік на велосипеді йому потрібно 12 хв, отже на шлях в один бік пішки він витратив 50-12=38 хв.
Увесь шлях в обидва кінці Вова пройде за 38х2=76 хв.

Відповідь: 76 хв.

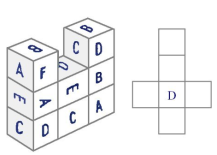
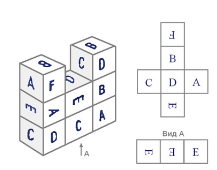Задача 12. Перед Вами споруда, яка складається із восьми однакових кубиків. А) Визначте розміщення букв на розгортці куба. (Відповідь намалюйте). Б) Визначте букви, які знаходяться в основі даної розгортки. (Відповідь намалюйте).

Зверніть увагу на поворот кожної букви.

Відповідь:

Задача 13. Петро, Геннадій, Дмитро та Володимир займаються у дитячій спортивній школі у різних секціях: гімнастичній, баскетбольній, волейбольній і легкої атлетики. Петро, Дмитро та волейболіст – однокласники. Петро та Геннадій ходять на тренування пішки, а гімнаст їде автобусом. Легкоатлет не знайомий ні баскетболістом, ні з волейболістом. Хто в якій секції тренується?

Розв’язання.

а) з першого твердження: волейболіст – не Петро і не Дмитро;

б) з другого твердження: гімнаст – не Петро і н Геннадій.

	волейбол	гімнастика	баскетбол	легка атлетика
Геннадій		-
Петро	-	-
Дмитро	-
Володимир

в) порівнюємо зміст першого і третього твердження і робимо висновок: так як Петро і Дмитро з волейболістом знайомі, а легкоатлет – не знайомий, то Петро і Дмитро не можуть займатися легкою атлетикою.

Після цього можна сказати: Петро відвідує баскетбольну секцію, а інші хлопці цю секцію не відвідують. Виходить: Дмитро – гімнаст.

	волейбол	гімнастика	баскетбол	легка атлетика
Геннадій		-	-
Петро	-	-	+	-
Дмитро	-	+	-	-
Володимир		-	-

г) Петро – баскетболіст, він знайомий з Геннадієм (з другого твердження), баскетболіст не знайомий з легкоатлетом (з третього твердження). Значить, Геннадій – не легкоатлет. Отже, Геннадій волейболіст, а Володимир – легкоатлет.

	волейбол	гімнастика	баскетбол	легка атлетика
Геннадій	+	-	-	-
Петро	-	-	+	-
Дмитро	-	+	-	-
Володимир	-	-	-	+

знак мира,люди,ромашки,символ мира,хиппи,цветы,шестидесятые годы дети,книги,люди,мальчики,очки Задача 14. Скількома способами можна розсадити у ряд на три стільці трьох учнів? Виписати всі можливі випадки.

люди,портфели,профессия,солнечные очки,художник фильма

Розв’язання.

Щоб виписати всі випадки, розв’язки можна представити у вигляді графа-дерева.

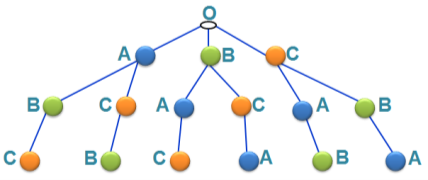
На перший стілець посадимо будь-якого учня: А, В, С. Якщо на першому стільці сидить учень А, то на другий стілець можна посадити В або С. Діємо аналогічно і для інших учнів. Очевидно, що третій стільчик в кожному випадку займе останній учень. Випишемо всі можливі випадки:

А-В-С, А-С-В, В-А-С, В-С-А, С-А-В, С-В-А.

Відповідь: 6.

Задача 15. Із настільної гри «Лото» взяли дві картки із цифрою 1 і три картки із цифрою 5. Скільки різних п’ятизначних чисел можно скласти із цих карток?

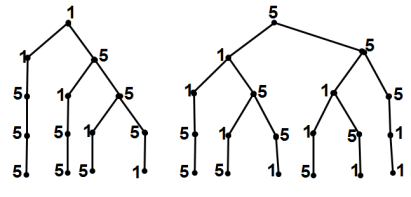
Відповідь: 10.

Середня оцінка розробки

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0

Загальна:

5.0

Всього відгуків: 1

Оцінки та відгуки

Гелбутовская Людмила 24.01.2020 в 10:56

Загальна:

5.0

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0

docx

Завантажити

Зберегти на потім

Додав(-ла)

Сапко Наталія Олександрівна

Пов’язані теми

Математика, 5 клас, Інші матеріали

Додано

10 листопада 2019

Переглядів

3776

Оцінка розробки

5.0 (1 відгук)