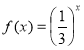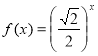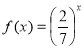Підсумкова контрольна робота

Про матеріал

Контрольна робота на 10 варіантів містить різнорівневі завдання. Призначена для перевірки підсумкових знань учнів з предмету.

Зміст архіву

Перегляд файлу

Комплексна контрольна робота зматематики

КВПУ гр.________________________________________________________

Прізвище, ім’я_____________________________________________________

Оцінка

Варіант 1

1. (1 бал). Визначте радіанну міру кута , який дорівнює 150^о.

А	Б	В	Г

2. (1 бал). Із наведених нижче функцій, показниковою є:

А	Б	В	Г

3. (1 бал) Якщо , то критичними для функції є точки:

10 і 0

-10 і 0

10 і -10

100 і -100

4. (1 бал). Точка D не лежить у площині трикутника АВС. Яке взаємне розміщення прямих ВD і АВ?

Мимобіжні

Паралельні

Перетинаються

Встановити не можливо

5. (1 бал). Переріз сфери діаметральною площиною є:

А	Б	В	Г
Точка	Великий круг	Велике коло	Визначити не можливо

6. (1 бал). У призмі, що має 12 ребер, в основі лежить:

Трикутник

Чотирикутник

Шестикутник

Інша фігура

7. (2,5 бали). Встановіть відповідність між рівнянням та його коренями.

1. 5^х-6=125;

2. 3^х+1+3^х=108.

А. -9; Розв’язання

Б. -3;

В. 3;

Г. 9.

Відповідь	1
Відповідь	2

8. (3 бали). Знайти проміжки спадання функції .

Розв’язання

Відповідь_______________________________

9.(3бали). Точка М знаходиться на відстані 2см від кожної зі сторін правильного трикутника АВС і на відстані 1см від його площини. Знайдіть сторону трикутника.

Розв’язання

Відповідь_______________________________

10. (3 бали). Радіус основи конуса дорівнює 4см, а відстань від центра його основи до твірної – 8см. Знайдіть висоту конуса.

Розв’язання

Відповідь_______________________________

Перегляд файлу

Комплексна контрольна робота з математики

(самоаналіз)

КВПУ гр.________________________________________________________

Прізвище, ім’я_____________________________________________________

Оцінка

Варіант 10

1. (1 бал). Якщо , то виконується умова:

А	Б	В	Г

2. (1 бал). Коренями рівняння є пара чисел:

А	Б	В	Г
3 і 3	2 і 10	-1 і 1	0 і -3

3. (1 бал). Радіанна міра кута 60^о дорівнює:

4. (1 бал). Яка з даних точок належить осі Z ?

М(0;-7;0)

N(8;0;0)

Р(8;0;1)

К(0;0;6)

5. (1 бал). Дано паралелограм АВСД і площину , прямі АС і ВД паралельні площині . Яке взаємне розташування прямої АВ і площини ?

А	Б	В	Г
Пряма перетинає площину	Пряма належить площині	Пряма паралельна площині	Встановити неможливо

6. (1 бал). Відстань між площинами основ циліндра називається:

Віссю циліндра

Висотою циліндра

Радіусом циліндра

Твірною циліндра

7. (2,5 бали). Укажіть для кожної функції відповідну їй похідну:

1. 2. .

А. ; Б. ;

Розв’язання

В. ; Г. .

Відповідь	1
Відповідь	2

8. (3 бали). Розв’яжіть нерівність .

Розв’язання

Відповідь_______________________________

9.(3бали). У правильній чотирикутній зрізаній піраміді висота дорівнює 2 см, а сторони основи 3 см і 5 см. Знайдіть діагональ цієї піраміди.

Розв’язання

Відповідь_______________________________

10. (3 бали). Відстань від точки S до кожної з вершин правильного трикутника АВС дорівнює 5 см, а до його площини – 3 см. знайдіть висоту трикутника.

Розв’язання

Відповідь_______________________________

Перегляд файлу

Комплексна контрольна робота з математики

КВПУ гр.________________________________________________________

Прізвище, ім’я_____________________________________________________

Оцінка

Варіант 2

1. (1 бал). Після спрощення вираз має вигляд:

А	Б	В	Г

2. (1 бал). Якщо , то виконується умова:

А	Б	В	Г

3. (1 бал). Із наведених нижче функцій зростаючою показниковою є:

4. (1 бал). Якщо в куб з ребром 10см вписано кулю, то її радіус дорівнює:

5см

10см

20см

Встановити не можливо

5. (1 бал). Знайти довжину відрізка СD, якщо С(6;-3;2), D(4;1;4).

А	Б	В	Г
24	2	8	4

6. (1 бал). У призмі, що має 6 вершин, в основі лежить:

Трикутник

Чотирикутник

Шестикутник

Інша фігура

7. (2,5 бали). Звільніть від радикала знаменник поданих дробів та вкажіть відповідні їм вирази.

1. ; 2. .

А. ; Розв’язання

Б. ;

В. ;

Г. .

Відповідь	1
Відповідь	2

8. (3 бали). Розв’яжіть рівняння

Розв’язання

Відповідь_______________________________

9.(3бали). Відстань від точки S до кожної з вершин правильного трикутника АВС дорівнює 5см, а до його площини – 3см. Знайдіть висоту трикутника.

Розв’язання

Відповідь_______________________________

10. (3 бали). Бічне ребро правильної шестикутної піраміди дорівнює 12см і утворює з площиною основи кут 60^о. Знайдіть площу бічної поверхні піраміди.

Розв’язання

Відповідь_______________________________

Перегляд файлу

Комплексна контрольна робота з математики

КВПУ гр.________________________________________________________

Прізвище, ім’я_____________________________________________________

Оцінка

Варіант 3

1. (1 бал). Значення дорівнює:

А	Б	В	Г
	0

2. (1 бал). За допомогою трьох різних цифр 5, 6, 7 можна утворити таку кількість двозначних чисел:

А	Б	В	Г
3	4	5	6

3. (1 бал). Градусна міра кута дорівнює:

90^о

60^о

45^о

30^о

4. (1 бал). Перерізом циліндра площиною, паралельною його осі, є:

Трикутник

Круг

Прямокутник

Встановити не можливо

5. (1 бал). Дано паралельні прямі а і в. Скільки існує площин, які проходять через пряму а і паралельні прямій в.

А	Б	В	Г
Одна	Дві	Безліч	Жодної

6. (1 бал). У призмі, що має 8 граней, в основі лежить:

Трикутник

Чотирикутник

Шестикутник

Інша фігура

7. (2,5 бали). Встановіть відповідність між рівнянням та його коренем.

1. 5^х-6=125; 2. 3^х+1+3^х=108.

А. -9; Розв’язання

Б. -3;

В. 3;

Г. 9.

Відповідь	1
Відповідь	2

8. (3 бали). Знайдіть екстремуми функції у=4х³-3х².

Розв’язання

Відповідь_______________________________

9.(3бали). Точки А(2;1;3), С(2;1;5), D(0;1;1) – вершини паралелограма АВСD. Знайдіть координати вершини В та довжини сторін паралелограма.

Розв’язання

Відповідь_______________________________

10. (3 бали). Бічне ребро правильної шестикутної піраміди дорівнює 12см і утворює з площиною основи кут 30^о. Знайдіть площу бічної поверхні піраміди.

Розв’язання

Відповідь_______________________________

Перегляд файлу

Комплексна контрольна робота з математики

КВПУ гр.________________________________________________________

Прізвище, ім’я_____________________________________________________

Оцінка

Варіант 4

1. (1 бал). Значення виразу дорівнює:

А	Б	В	Г
1	3	-5	-3

2. (1 бал). Коренями рівняння є пара чисел:

А	Б	В	Г
-1 і 1	3 і 1	-8 і 12	-2 і 2

3. (1 бал). За допомогою трьох різних цифр 4, 5, 6 можна утворити таку кількість двозначних чисел:

4. (1 бал). Прямий циліндр можна розглядати як тіло, утворене в результаті обертання прямокутника навколо

Сторони

Діагоналі

Вершини

Інша відповідь

5. (1 бал). Перпендикуляр, опущений із вершини конуса на площину його основи, називається:

А	Б	В	Г
Твірною конуса	Висотою конуса	Віссю конуса	Радіусом конуса

6. (1 бал). Знайти координати вектора , якщо

(-6;6;1)

(2;-10;-1)

(-10;14;2)

(-18;20;3,5)

7. (2,5 бали). Встановіть відповідність між рівнянням та його коренем.

1. ;

2. .

А. -12; Розв’язання

Б. -4;

В. 4;

Г. 12.

Відповідь	1
Відповідь	2

8. (3 бали). Знайдіть найбільше і найменше значення функції

Розв’язання

Відповідь_______________________________

9.(3бали). Основа прямої призми – ромб із діагоналями 4 і 2см. Обчисліть площу бічної поверхні призми, якщо її менша діагональ нахилена до площини основи під кутом 45^о.

Розв’язання

Відповідь_______________________________

10. (3 бали). Довжина лінії перетину сфери і площини, віддаленої від її центра на 12см, дорівнює 10см. Знайдіть довжину великого кола сфери.

Розв’язання

Відповідь_______________________________

Перегляд файлу

Комплексна контрольна робота з математики

КВПУ гр.________________________________________________________

Прізвище, ім’я_____________________________________________________

Оцінка

Варіант 5

1. (1 бал). Виберіть точку, через яку проходить графік функції у=2^х+1.

А	Б	В	Г
М(3;7)	N(3;9)	K(4;8)	P(4;9)

2. (1 бал). Для функції знайти у

А	Б	В	Г

3. (1 бал). Якщо , то функція спадає на проміжку:

4. (1 бал). Зрізаний конус можна розглядати як тіло, утворене в результаті обертання прямокутної трапеції навколо її:

Більшої бічної сторони

Основи

Меншої бічної сторони

Висоти

5. (1 бал). Перерізом циліндра площиною, паралельною його основі, є:

А	Б	В	Г
Трикутник	Круг	Прямокутник	Коло

6. (1 бал). Пряма m проходить через середину сторони АВ трикутника АВС. Яке взаємне розташування прямих m і ВС, якщо пряма m не лежить у площині АВС?

Мимобіжні

Перетинаються

Паралельні

Встановити не можливо

7. (2,5 бали). Знайдіть для кожного з рівнянь відповідні корені.

1. ; 2.

А. ; Розв’язання

Б.

В. ;

Г. .

Відповідь	1
Відповідь	2

8. (3 бали). Розв’яжіть рівняння

Розв’язання

Відповідь_______________________________

9.(3бали). Площа перерізу кулі площиною, віддаленою від її центра на 15см, дорівнює 64см². Знайдіть площу великого круга.

Розв’язання

Відповідь_______________________________

Розв’язання

Відповідь_______________________________

Перегляд файлу

Комплексна контрольна робота з математики

КВПУ гр.________________________________________________________

Прізвище, ім’я_____________________________________________________

Оцінка

Варіант 6

1. (1 бал). Значення виразу дорівнює:

А	Б	В	Г
0,016	40	400	5

2. (1 бал). Після спрощення вираз має вигляд:

А	Б	В	Г

3. (1 бал) Якщо , то функція спадає на проміжку:

4. (1 бал). Точка М лежить поза площиною трикутника АВС. Яке взаємне розташування прямих АВ і МС?

Перетинаються

Паралельні

Мимобіжні

Встановити не можливо

5. (1 бал). Яка з точок належить осі х?

А	Б	В	Г
А(0;1;0)	В(0;0;4)	С(-1;0;0)	Д(1;2;0)

6. (1 бал). Площа поверхні куба з ребром 5 см дорівнює:

150см²

100см²

25см²

Інша відповідь

7. (2,5 бали). Встановіть для кожного модуля відповідне йому значення.

А. Розв’язання

Б.

В.

Г.

Відповідь	1
Відповідь	2

8. (3 бали). З 4 учнів потрібно вибрати трьох для виступу в святковому концерті. Скільки варіантів вибору цих трьох учнів існує?

Розв’язання

Відповідь_______________________________

9.(3бали). Висота циліндра дорівнює 8 см, а радіус основи – 5 см. На відстані 4 см від осі циліндра паралельно їй проведено площину. Знайдіть діагональ утвореного перерізу.

Розв’язання

Відповідь_______________________________

10. (3 бали). Знайдіть площу великого круга кулі, якщо площа перерізу кулі площиною, віддаленою від її центра на 12 см, дорівнює 64см².

Розв’язання

Відповідь_______________________________

Перегляд файлу

Комплексна контрольна робота з математики

КВПУ гр.________________________________________________________

Прізвище, ім’я_____________________________________________________

Оцінка

Варіант 7

1. (1 бал). Обчисліть : 4!+3!

А	Б	В	Г
7	12	15	30

2. (1 бал). Укажіть правильну рівність.

А	Б	В	Г

3. (1 бал). Після спрощення Вираз має вигляд:

4. (1 бал). Площа бічної поверхні куба з ребром 5 см дорівнює:

150см²

100см²

25см²

Інша відповідь

5. (1 бал). Тіло, що утворюється при обертанні півкруга навколо його діаметра, називається:

А	Б	В	Г
Кругом	Сферою	Кулею	Колом

6. (1 бал). Дано мимобіжні прямі а і в. Скільки існує площин, які проходять через пряму а і паралельні прямій в?

одна

дві

безліч

жодної

7. (2,5 бали). Укажіть для кожної функції відповідну їй похідну:

1. 2.

А. Б.

Розв’язання

В. Г. .

Відповідь	1
Відповідь	2

8. (3 бали). Розв’яжіть нерівність .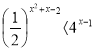

Розв’язання

Відповідь_______________________________

9.(3бали). У кулі на відстані 5 см від центра О проведено січну площину, радіус перерізу дорівнює 12 см. Знайдіть залежність площ від їх радіусів.

Розв’язання

Відповідь_______________________________

10. (3 бали). Висота конуса дорівнює 20 см, а відстань від центра його основи до твірної – 12 см. Знайдіть радіус конуса.

Розв’язання

Відповідь_______________________________

Перегляд файлу

Комплексна контрольна робота з математики

КВПУ гр.________________________________________________________

Прізвище, ім’я_____________________________________________________

Оцінка

Варіант 8

1. (1 бал). Розв’язком нерівності є проміжок:

А	Б	В	Г

2. (1 бал). Знайдіть значення .

А	Б	В	Г

3. (1 бал). За допомогою трьох різних цифр 9, 8, 7 можна утворити таку кількість двозначних чисел:

4. (1 бал). Записати координати вектора , якщо М(2;4;-3) і К(8;1;0)

(10;5;-3)

(-6;3;-3)

(6;-3;3)

(16;4;0)

5. (1 бал). Діагональ прямокутного паралелепіпеда з вимірами 1, 1 і см дорівнює:

А	Б	В	Г
3см	4см	5см	Інша відповідь

6. (1 бал). Якщо в куб з ребром 10 см вписано кулю, то її діаметр дорівнює:

5см

10см

20см

30см

7. (2,5 бали). Укажіть відповідність між рівнянням та його коренями.

1. 2. .

А. -2; Б. -1;

Розв’язання

В. 1; Г. 2.

Відповідь	1
Відповідь	2

8. (3 бали). Знайдіть екстремуми функції .

Розв’язання

Відповідь_______________________________

9.(3бали). Точки В(2;1;3), С(1;1;4), Д(0;1;3) – вершини паралелограма АВСД. Знайдіть координати вершини А та довжини сторін паралелограма,

Розв’язання

Відповідь_______________________________

10. (3 бали). Довжина лінії перетину сфери і площини, яка віддалена від її центра на

12 см, дорівнює 10см. Знайдіть площу діаметральної площини.

Розв’язання

Відповідь_______________________________

Перегляд файлу

Комплексна контрольна робота з математики

КВПУ гр.________________________________________________________

Прізвище, ім’я_____________________________________________________

Оцінка

Варіант 9

1. (1 бал). Якщо, то критичними для функції є точки:

А	Б	В	Г
-64 і 0	64 і 0	-8 і 8	-32 і 32

2. (1 бал). ЗнайдітьР₆.

А	Б	В	Г
6	21	44	720

3. (1 бал). Обчисліть.

-3

4. (1 бал). Діагональ прямокутного паралелепіпеда з вимірами , 2 і 3 дорівнює:

3см

4см

5см

Інша відповідь

5. (1 бал). Діагоналі паралелограма паралельні площині . Яке взаємне розміщення площини і площини паралелограма?

А	Б	В	Г
Збігаються	Перетинаються	Паралельні	Встановити неможливо

6. (1 бал). Перпендикуляр опущений із вершини конуса на площину його основи, називається:

Твірною конуса

Висотою конуса

Віссю конуса

Інша відповідь

7. (2,5 бали). Вкажіть відповідність між рівнянням та його коренем:

1. 2. .

А. -1; Б. 1;

Розв’язання

В. 2; Г. 3.

Відповідь	1
Відповідь	2

8. (3 бали). Розв’яжіть рівняння .

Розв’язання

Відповідь_______________________________

9.(3бали). З точки, віддаленої від площини на 8 см, проведено дві похилі під кутом 45^о до площини. Знайдіть відстань між основами похилих, якщо кут між їх проекціями дорівнює 120^о.

Розв’язання

Відповідь_______________________________

10. (3 бали). Сторона основи правильної чотирикутної піраміди дорівнює 2 см, а висота пірамідисм. Знайти площу бічної поверхні піраміди.

Розв’язання

Відповідь_______________________________

zip

Завантажити

Зберегти на потім

Додав(-ла)

Жуйкова Наталія Миколаївна

Пов’язані теми

Математика, 11 клас, Контрольні роботи

Додано

28 лютого 2019

Переглядів

2580

Оцінка розробки

Відгуки відсутні