Творчий проект на тему "Правильні многогранники"
Київське вище професійне училище будівництва і дизайну
 Творчийпроект
Творчийпроект
на тему :
«Правильні многогранники»
Підготувала: викл. математики Р.І. Максимчук
http://presentation-creation.ru/
Девіз проекту:
Найвище призначення математики полягає в тому, щоб знаходити
прихований порядок в хаосі, що оточує нас
Н. Вінер
Мета проекту:
Практична:
• сформувати в учнів уявлення про існування математичних форм в оточуючому світі;
• розширити і поглибити знання дітей про многогранники та використання їх у природі, архітектурі та в творчості;
• удосконалити та розвивати творчі здібності учнів, уміння застосовувати математичні знання у творчій діяльності;
• Формувати вміння аналізувати інформацію, аналізувати особисті пізнавальні та практичні дії;
• Налагодження міжособистісної взаємодії шляхом зовнішнього діалогу в процесі засвоєння учбового матеріалу;
• Підвищувати рівень активності і самостійності;
• Формувати вміння і навики роботи з Інтернет – ресурсами, розвивати спеціальні дослідницькі вміння і навики.
Освітня:
• Поглибити знання учнів про правильні многогранники;
• Показати значення правильних многогранників з історичної і математичної точки зору;
• Показати взаємозв’язок вивчених на уроці тем з навколишнім світом і оточуючим нас побутом.
Розвиваюча:
• Розвивати пізнавальний інтерес до математики;
• Розвивати художнє бачення, навички режисури;
• Сприяти вихованню активного мислення, комунікативних якостей учнів; Виховна:
• Виховувати творче мислення, всебічно розвинуту особистість;
• Виховувати естетичний смак, уміння цінувати прекрасне;
• Активізувати пізнавальну діяльність учнів, виховувати любов до предмету.
Завдання проекту:
• дослідити «присутність» правильних многогранників в природі та побуті;
• довести необхідність вивчення геометрії для практичного застосування у житті;
• підготувати експозицію творчих робіт учнів;
• зробити презентацію та провести захист проекту.
І Підготовчий етап
«Скажи мені – і я забуду, покажи мені – і я запам’ятаю, дай зробити – і я зрозумію»
Історики – вивчають значення правильних многогранників з історичної і математичної точки зору
Теоретики-дослідники – вивчають матеріал з підручника та додаткових джерел та досліджують застосування многогранників в природі та архітектурі
Практики – виготовляють моделі правильних многогранників для наочності
 |
 |
||
ІІ Відбір матеріалу

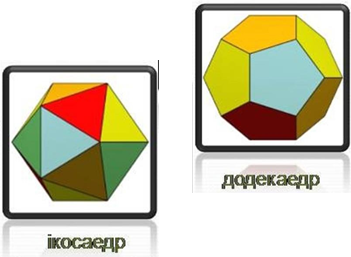
Правильним многогранником є многогранник, грані якого є правильними многокутниками з рівною кількістю сторін, а в кожній вершині многогранника сходиться однакова кількість ребер.
Існує п’ять типів правильних опуклих многогранників: правильний тетраедр, куб, октаедр, додекаедр, ікосаедр.
Історія
Перші згадки про многогранники відомі ще за три тисячі років до нашої ери в Єгипті і Вавилоні.
 Але
теорія многогранників є і сучасним розділом математики. Вона тісно
пов’язана з топологією, має велике значення як для теоретичних досліджень по
геометрії, так і для практичних застосувань в інших розділах
Але
теорія многогранників є і сучасним розділом математики. Вона тісно
пов’язана з топологією, має велике значення як для теоретичних досліджень по
геометрії, так і для практичних застосувань в інших розділах
математики, наприклад, в алгебрі, теорії чисел, прикладній математиці – лінійному програмуванні, теорії оптимального управління.
 Фалес Мілетський (624-548
рр. до н.е.)
Фалес Мілетський (624-548
рр. до н.е.)
Учені і філософи Древньої Греції сприйняли і переробили досягнення культури і науки Древнього Сходу. Не випадково зачатки грецької геометричної науки пов’язані з ім’ям Фалеса Мілетського, засновника іонійської школи. Учені іонійської школи уперше піддали логічній обробці і систематизували математичні відомості, запозичені у давньосхідних народів, особливо у
вавілонян
 Піфагор (580-500 рр. до
н.е.)
Піфагор (580-500 рр. до
н.е.)
Найвідомішою школою Давньої Греції була Піфагорійська, названа на честь свого засновника Піфагора (570–470 р. до н.е.). Відмітним знаком піфагорійців була пентаграма, на мові математики – це правильний неопуклий або зірчастий п’ятикутник.
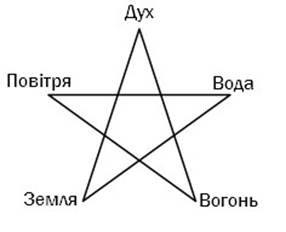 Пентаграмі привласнювалася здатність
оберігати людину від злих духів. Існування тільки п’ять правильних
многогранників: тетраедр, куб, октаедр, додекаедр, ікосаедр, відносили до
будови матерії і Всесвіту.
Пентаграмі привласнювалася здатність
оберігати людину від злих духів. Існування тільки п’ять правильних
многогранників: тетраедр, куб, октаедр, додекаедр, ікосаедр, відносили до
будови матерії і Всесвіту.
 Подальший розвиток многогранників пов’язаний з
Евклідом. Основним його твором є «Начала». Створюючи свій підручник, Евклід
включив до нього багато з того, що було створене його попередниками, обробивши
цей матеріал і звівши його воєдино.
Подальший розвиток многогранників пов’язаний з
Евклідом. Основним його твором є «Начала». Створюючи свій підручник, Евклід
включив до нього багато з того, що було створене його попередниками, обробивши
цей матеріал і звівши його воєдино.
 Услід за Евклідом вивченням правильних
многогранників займався Архімед.
Услід за Евклідом вивченням правильних
многогранників займався Архімед.
Переконавшись в тому, що не можна побудувати шостий многогранник, Архімед став будувати многогранники, у яких гранями є правильні, але не однойменні багатокутники, а в кожній вершині, як і у правильних многогранників, сходиться одне і те ж число ребер. Вийшли так звані напівправильні многогранники.
Напівправильні многогранники Архімеда

Ілюстрації Леонардо да Вінчі

 В епоху
відродження великий інтерес до форм правильних многогранників виявили
скульптори, архітектори, художники.
В епоху
відродження великий інтерес до форм правильних многогранників виявили
скульптори, архітектори, художники.
Леонардо да Вінчі захоплювався теорією многогранників і часто зображував їх на своїх полотнах.
 Іоганн Кеплер (1571-1630)
Іоганн Кеплер (1571-1630)

 Серед учених, що досліджували
многогранники, особливе місце належить Іоганну Кеплеру, який написав етюд
«Про сніжинку», в якому висловив таке зауваження:
Серед учених, що досліджували
многогранники, особливе місце належить Іоганну Кеплеру, який написав етюд
«Про сніжинку», в якому висловив таке зауваження:
«Серед правильних тіл найперше, початок і батько інших – куб, а його, якщо дозволено так би мовити, дружина – октаедр, бо у октаедра стільки кутів, наскільки у куба граней».
Кеплер першим опублікував повний список тринадцяти архімедівських тіл і дав їм ті назви, під якими вони відомі понині
 Леонард Ейлер
Леонард Ейлер
(1707-1783)
Відомий швейцарський математик Ейлер відкрив і довів знамениту формулу
В – Р + Г = 2
що зв’язує числа вершин, ребер і граней будь-якого опуклого многогранника.
Ідеї Піфагора, Платона, Кеплера про зв’язок правильних багатокутників з гармонійним устроєм світу і у наш час знайшли своє продовження в цікавій науковій гіпотезі, яку висловили вчені на початку ХХ століття.
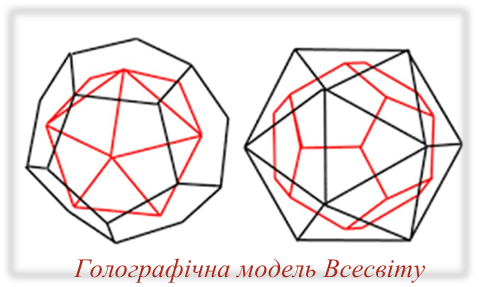 Вони
вважають, що ядро Землі має форму і властивості зростаючого кристала, що
робить дію на розвиток усіх природних процесів, що йдуть на планеті.
Вони
вважають, що ядро Землі має форму і властивості зростаючого кристала, що
робить дію на розвиток усіх природних процесів, що йдуть на планеті.
Промені цього кристала, а точніше його силове поле, обумовлюють ікосаедро-додекаедрову структуру Землі. Вона проявляється в тому, що в земній корі як би проступають проекції вписаних в земну кулю правильних многогранників: ікосаедра і додекаедра.
Правильні многогранники в природі
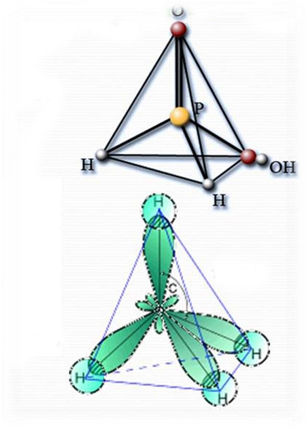
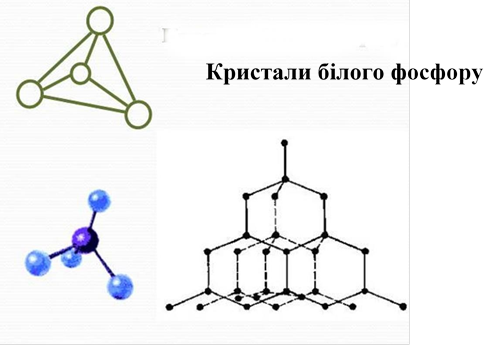 Тетраедр в природі
Тетраедр в природі
Будова решітки кристалу алмаза
Кристалічна решітка метану
Октаедр в природі
 Вуглець (С)
характеризується
Вуглець (С)
характеризується
структурою октаедра
Кристали
алмаза 
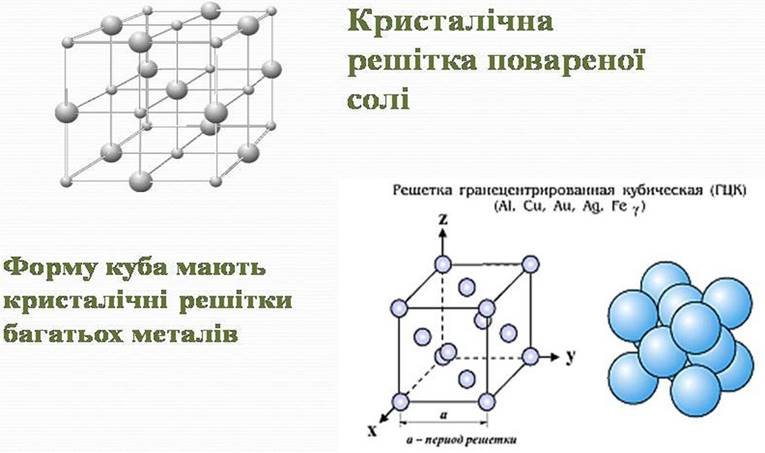
Куб в природі
Ікосаедр в природі

Додекаедр в природі


архітектурі
архітектурі
 Білоруська
національна
Білоруська
національна 
Адміністрація міської
республіканська бібліотеки в Ніцці
бібліотека
архітектурі

Будинок у Словаччині: на з’єднаних між собою тумбах стоять на ребрах кубики.
Кожен кубик – триярусна квартира
ІІІ етап
(практичне завдання)


ДЯКУЮ ЗА УВАГУ!!!


про публікацію авторської розробки
Додати розробку
