Підсумковий урок з геометрії у 11 класі. "Розв'язування прикладних задач з теми площі та об'єми тіл обертання"

Розв’язування прикладних задач з теми площі та об’єми тіл обертання

Мета:

навчальна: систематизувати та узагальнити знання учнів з теми «Тіла обертання»; підвищити рівень сформованості знань, умінь та навичок розв’язувати задачі з теми; формувати вміння застосовувати набуті знання під час розв’язування практичних задач;

розвивальна: сприяти розвитку систематичних знань, логічного мислення учнів, обчислювальних навиків, математичної мови; розвивати просторове уявлення, уміння спостерігати та аналізувати навколишні явища. Формувати в учнів дослідницькі компетентності, соціальні, саморозвитку і самоосвіти, інформаційні та комунікативні;

виховна: виховувати культуру спілкування, працьовитість, колективізм, відповідальність та вимогливість за виконану справу, підвищувати інтерес до вивчення математики.

Тип уроку: узагальнення та систематизація знань.

Обладнання: комп’ютер; презентація; моделі тіл обертання; таблиці; тенісні кульки, метр, лінійка, штангенциркуль, мотузка.

Епіграф уроку: Не достатньо мати лише добрий розум, головне – це раціонально застосувати його.

Рене Декарт.

Хід уроку

І. Організаційно-психологічна частина.

• налаштування учнів на продуктивну роботу на уроці;
• перевірка готовності до уроку;
• перевірка виконання ортопедичного режиму;
• розподіл учнів на групи;

Хвилина відпочинку.

 «Математичний жарт»

Протягом року вам майже ніколи вчитися. У році 365 днів, з них 52 дні неділі і 10 днів державних свят – тобто 62 дні ви разом з близькими відпочиваєте. Зимові і літні канікули не менше 100 днів, тому ви не вчитеся 162 дні. Вночі ви також не вчитеся і це ще півроку – тобто 182 дні. Отже, залишається 20 днів, але заняття у школі тривають не весь день, а лише не більше півдня, тому ще відпадає 10 днів. Залишається лише 100 днів напруженої праці, коли можна отримати глибокі знання. Я гадаю це вам під силу! Тож розпочинаємо свою роботу.

Намагайтесь щодня для кожної справи знайти якийсь позитивний початок, оскільки від настрою, з яким ви розпочинаєте день або якусь справу, залежать ваші успіхи, а, можливо, і невдачі. А я сподіваюсь що у кожного присутнього зараз чудовий настрій.

ІІ. Мотивація навчальної діяльності.

Антична мудрість стверджує «Знання – це сила». На мою думку, знання – це одна із сходинок до успіху в майбутньому. І сьогодні ми будемо плідно працювати, щоб досягнути мети. Отож метою нашого уроку є узагальнення та систематизація знань, умінь та навичок з теми «Тіла обертання. Розв’язування прикладних задач».

ІІІ. Актуалізація опорних знань (використовуємо «асоціативний кущ»).

 

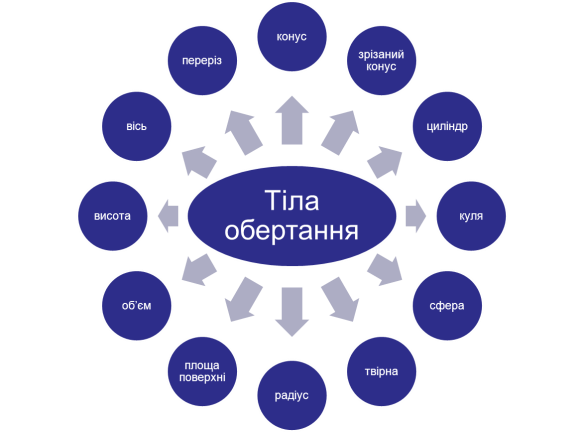
Гра «Мікрофон»

Що можна знайти за допомогою цих формул

«Ти мені, а я тобі»

Питання:

1. Що в перекладі з грецької означає «циліндр»? (коток)
2. Пряма, навколо якої обертається прямокутник? (вісь)
3. Фігура обертання, яка утворюється при обертанні круга навколо його діаметра? (куля)
4. Поверхня кулі? (сфера)
5. Розділ геометрії, в якому вивчаються фігури у просторі? (стереометрія)
6. Добуток площі основи циліндра на його висоту? (об'єм)
7. Розгортка бічної поверхні конуса? (сектор)
8. Основа конуса? (круг)
9. Катет, навколо якого обертається прямокутний трикутник, називається … конуса? (висотою)
10. Перпендикуляр, проведений з довільної точки однієї основи до другої основи циліндра? (висота)
11. Гіпотенуза прямокутного трикутника, яка описує бічну поверхню конуса? (твірна)
12. Розгортка бічної поверхні циліндра? (прямокутник)
13. Футбольна «куля»? (м’яч).
14. Осьовий переріз  зрізаного конуса ( рівнобічна трапеція)
15. Яке тіло утвориться обертанням навколо своєї осі симетрії рівнобічної трапеції. (зрізаний конус)

     Вдосконалення знань і вмінь                                       

Ще зовсім трішки і кожен з вас розпочне нове життя здобуваючи майбутню професію. Звичайно, щоб оволодіти певною професією необхідно вступити до відповідного навчального закладу . Зараз ми перевіримо як кожен із вас готовий до ЗНО.

Індивідуальна робота

 Гра «Готуємось до ЗНО» в подальшою самоперевіркою

1)Квадрат обертається навколо своєї сторони. Знайти об’єм тіла обертання,якщо сторона квадрата 2 см.(в)

А	Б	В	Г	Д
8π/3 см.куб	4π см куб.	8π см куб.	2π см куб.	16πсм куб.

 

2)Твірна конуса у 2 рази більша від його радіуса. Знайти кут нахилу твірної конуса до площини його основи.(Г)

А	Б	В	Г	Д
90°	45°	30°	60°	50°

 

3)Осьовий переріз циліндра є квадратом ,а довжина кола основи 12π см. Знайдіть площу перерізу.(А)

А	Б	В	Г	Д
144	36	64	576	24

4)Металеву кульку,радіус якої 6 см,переплавили в конуси однакового розміру з висотою 3 см і радіусом основи 2 см. Скільки таких конусів одержали?Втратами металу при переплавленні знехтуйте.(Б)

А	Б	В	Г	Д
24	72	12	36	144

Заповніть відповідний бланк

Гра «Відповідність » робота в парах з подальшою взаємоперевіркою 

На рисунку зображений конус,у якого діаметр основи дорівнює твірній. Установіть відповідність   між заданим кутом (1-4) і їх градусними мірами (а-д)

 

КУТ	ГРАДУСНА МІРА КУТА
1.Кут між висотою конуса та його твірною	А.90°
2.Кут між твірною SN і площиною основи конуса	Б.80°
3.Кут радіусами основи АО і ОN,якщо дуга BN=100°	В.30°
4.Кут між прямими SO і ON	Г.40°
	Д.60°

 

           S

 

 

 

 

 

                       В

 

 

 

 

	А	Б	В	Г	Д
1			*
2					*
3		*
4	*

А                    N

 

 

 

 

 

 

 

 

В житті ми майже щодня зустрічаємо різні предмети у формі тіл обертання. Тож давайте пригадаємо їх. (учні по черзі називають предмети )

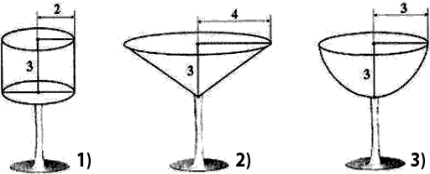
Задача. В який із запропонованих фужерів можна налити найбільше рідини?

 

1. 

.

2. 

.

3. 

.

Отже, як ми бачимо найбільший об’єм має півкуля.

Робота в групі хто швидше розв’яже задачі 

Задача . Скільки потрібно квадратних сантиметрів шкіри, щоб зробити покришку    для футбольного м’яча? (На шви і обрізки додати 5% матеріалу).

Розв'язання:

Діаметр футбольного м’яча стандартний – він дорівнює 25 см.

;

.

Обчислимо 5% від даної площі (м²).

Отже, всього потрібно матеріалу: 0,196+0,0098=0,206 (м²)=2060 (см²).

Відповідь:  2060 см² .

      Задача.  Що вигідніше: купити кавун радіусом 30см і з’їсти у п’ятьох,

чи купити три кавуни діаметром по 20см і поділити на двох?

Розв’язання.

Об’єм кавуна обчислимо за формулою об’єму кулі:

V= R

Об’єм великого кавуна  R=30см  дорівнює

V= 30 = 27000= 36000 (см )

36000  : 5 = 7200 ( см ) – кожному.

Об’єм трьох малих кавунів  R=d:2=10 см  дорівнює

V=3 10 = 4000 ( см )

4000 : 2= 2000 ( см ) – кожному.

Відповідь: один R=30 см.                         

Хвилина відпочинку

Після гарної роботи необхідний відпочинок. Тож я пропоную вам трішки відпочити але цей відпочинок буде  корисним та пізнавальним, увага на екран.

Перегляд відео про 23 лютого день заснування тенісу

 

Теніс популярна гра і сьогодні, наші вихованці часто влаштовують змагання . а чи не замислювалися ви який об’єм  та площу має ця кулька. Тож я пропоную вам за допомогою всіх можливих приладів визначити об’єм цих тенісних кульок.

 

Д1= 6,7 см

 

Д2 =4 мм

 

 

 

 

Молодці справилися із завданням.

В житті ми майже щодня зустрічаємо різні предмети у формі тіл обертання. Тож давайте пригадаємо їх.

А чи знаєте ви, що найдорожчий Платиновий торт  вартістю $130 тис. має форму циліндру. Цей торт прикрашений ювелірними виробами з платини

Платиновий торт, створений знаменитим японським кондитером Нобуе Ікара, коштує не менше автомобіля класу «люкс»: 130 тисяч доларів! Зверху виріб покрито простою білою глазур’ю і декороване десятками ланцюжків, кулонів і шпильок, зроблених з платини найвищої проби. Ікара присвятив цей кондитерський шедевр всім представницям прекрасної статі і конкретно японської актрисі Ринко Кикути. Платиновий торт був створений за замовленням корпорації Platinum Guild International, що спеціалізується на продажу ювелірних прикрас з цього дорогоцінного металу. Компанія розраховувала, що це виріб послужить відмінною рекламою їх продукції.

Жодна жінка на мій погляд не може встояти перед цим маленьким смачненьким десертом. Здогадалися про який десерт йдеться. Звичайно ж Макаруни.  Найдорожчі макаруни у світі Haute Couture ($7,5 тис.)

Макаруни – мигдальне печиво з найніжнішим смаком і прошарком з вершкового крему. Це ласощі популярним у Франції. В кондитерському відділі будь-якого магазину ви без праці зможете знайти десятки видів макарун. У 2008 році французький кондитер П’єр Ерме видозмінив оригінальний рецепт ласощів. За словами П’єра, він готує авторські макаруни виключно з високоякісних і, відповідно, дорогих продуктів, чим і обумовлюється запаморочлива ціна ласощі – майже 7,5 тисяч доларів за кілограм! Клієнти мають можливість вибирати інгредієнти для майбутніх макарун на свій розсуд. Великою популярністю користуються такі незвичайні складові, як бальзамічний оцет, біле і червоне вино, а також морська сіль.

Санде "Золотий достаток". Ресторан "Serendipity 3" може запропонувати смачне блюдо. Це морозиво з фруктами можна покуштувати в Нью-Йорку на свій золотий ювілей - 50-річчя, а обійдеться десерт не 50, а в 1000 доларів. У ресторані стверджують, що за місяць продається лише одне морозиво, але це ж краще, ніж нічого, правда? Морозиво відомо, як найдорожче  у світі. У нього входять 5 порцій таїті ванільного, змішаного з мадагаскарської ванілі і венесуельським шоколадом Chuao, покритого їстівним 23-каратним золотом. У число інших інгредієнтів входять золоті драже, паризькі зацукровані фрукти, марципани і трюфелі. Верху всього пишноти розміщується одна з найбільш дорогих цукерок у світі - Amedei Porcelana, і цукровий квітка. На вершині морозива розташовується в невеликій мисці ікра, підсолоджена маракуйєю, арманьяком і пофарбована в золотистий колір. Щоб повністю відповідати стилю страви до нього подається золота ложка і кубок з кришталю Харкурт. Популярність сандэ була така велика, що воно стало невід'ємною частиною серіалу "Студія 30".

   Підсумок уроку

Хочу наголосити на всебічному застосуванні математики. Її використовують у всіх галузях практичної діяльності людини. Сьогодні ми повторили формули для обчислення площ поверхонь та об’ємів тіл обертання, застосували ці знання, вміння та навики при розв’язування задач з прикладним змістом. Наше суспільство потребує як талановитих дослідників, так і спеціалістів, які добре знають математику та здатні застосувати свої знання на практиці.

Рене Декарт сказав: «Теорія без практики мертва і безплідна, практика без теорії неможлива». Важко з цим не погодитись.

Хочу подякувати за роботу на уроці та підготовку до уроку………….. .

Здайте зошити для перевірки та отримання оцінки.

Ну а на останок я хочу пригостити вас солодощами у формі різних тіл обертання. Нехай кожен вибере собі по душі та отримає своє побажання на найближче майбутнє.

Домашнє завдання : підготувати творчі проекти з теми тіла обертання.    

 

Дякую за увагу, до нових зустрічей.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Бланк  відповідей здобувача освіти 11 класу

______________________________________

 

Тестові завдання

	А	Б	В	Г	Д
1
2
3
4

Завдання на встановлення відповідності

	А	Б	В	Г	Д
1
2
3
4

 

 

Бланк  відповідей здобувача освіти 11 класу

______________________________________

 

Тестові завдання

	А	Б	В	Г	Д
1
2
3
4

Завдання на встановлення відповідності

	А	Б	В	Г	Д
1
2
3
4

 

 

 

 

 

 

 

 

 

 

Гра «Готуємось до ЗНО» в подальшою самоперевіркою

1)Квадрат обертається навколо своєї сторони. Знайти об’єм тіла обертання,якщо сторона квадрата 2 см.

А	Б	В	Г	Д
8π/3 см.куб	4π см куб.	8π см куб.	2π см куб.	16πсм куб.

 

2)Твірна конуса у 2 рази більша від його радіуса. Знайти кут нахилу твірної конуса до площини його основи.

А	Б	В	Г	Д
90°	45°	30°	60°	50°

 

3)Осьовий переріз циліндра є квадратом ,а довжина кола основи 12π см. Знайдіть площу перерізу.

А	Б	В	Г	Д
144	36	64	576	24

4)Металеву кульку,радіус якої 6 см,переплавили в конуси однакового розміру з висотою 3 см і радіусом основи 2 см. Скільки таких конусів одержали?Втратами металу при переплавленні знехтуйте.

А	Б	В	Г	Д
24	72	12	36	144

Заповніть відповідний бланк

Гра «Відповідність » робота в парах з подальшою взаємоперевіркою 

На рисунку зображений конус,у якого діаметр основи дорівнює твірній. Установіть відповідність   між заданим кутом (1-4) і їх градусними мірами (а-д)

КУТ	ГРАДУСНА МІРА КУТА
1.Кут між висотою конуса та його твірною	А.90°
2.Кут між твірною SN і площиною основи конуса	Б.80°
3.Кут радіусами основи АО і ОN,якщо дуга BN=100°	В.30°
4.Кут між прямими SO і ON	Г.40°
	Д.60°

                           S

 

 

 

 

 

                                   B

 

                                           

                            O                   N

 

                                                                               A