Підсумковий урок "Звичайні дроби"

ПІДСУМКОВИЙ УРОК ЗА ТЕМОЮ «ЗВИЧАЙНІ ДРОБИ»

Мета: навчити поєднувати математичну і нематематичну інформацію, удосконалювати знання учнів про звичайні дроби; розвивати логічне мислення, навички усної лічби, математичну мову; виховувати інтерес до нових знань і прагнення їх набувати.

Обладнання: планшети, тести.

                                                  Хід уроку

І. Організаційний момент

 

ІІ. Повідомлення теми, мети уроку.

 

Ш.Історичні повідомлення ( готують учні )      

1. Дробові числа в Єгипті були відомі ще 4000 років потому. Записували їх тоді тільки одиничними дробами( тобто такими ,чисельники яких дорівнюють одиниці) або сумами одиничних дробів. Наприклад, дріб 2/5 єгиптяни писали 1/3 + 1/15 , а дріб 2/13 у вигляді суми 1/8 , 1/52 і 1/104.

2.ажливими і найбільш вживаними були дроби .Такі дроби відіграли визначну роль у музиці. І сьогодні в загальноприйнятому запису найдовша за звучанням ціла нота ділиться на половини, чверті, восьмі, шістнадцяті.

3 Давньогрецькі математики розглядали числа, які зараз  записують у вигляді дробів, але називали їх відношеннями. Римляни користувалися дробами із знаменниками 12, які називали унціями. Коли казали «5 унцій» або «13 унцій» , то мали на увазі 5/12 або 13/12.

4.У Китаї дроби називали , користуючись словом «половина» : .У  Греції  та Єгипті довгий час користувались дробами з чисельником 1, вавілоняни із знаменником 60.

5. Слова «чисельник» і «знаменник» вперше з’явились в ХІІІ ст., «скорочення дробу» і «зведеня дробів до спільного знаменника» - в ХV ст.., а «правильні» і «неправильні» дроби – в ХVІІІ. В Україні спочатку використовували тільки одиничні дроби. Але й зараз дроби називають «половиною», «третиною», «четвертиною» . Числа 1 - півтора, 2- пів третина, 4- пів п’ята.

 

  IV. Актуалізація опорних знань

А) Фронтальне опитування учнів :

1.Які числа називаються звичайними дробами?

2.Що позначає риска дробу?

3 Що називається знаменником дробу і на що він вказує?

4.Що називається чисельником дробу і на що він вказує?

5.Який дріб називається правильним?

6.Який дріб називається неправильним?

7. записати у вигляді правильного дробу.

8. записати у вигляді неправильного дробу.

Б) Робота на планшетах:

1. Записати неправильний дріб із знаменником 5.

2. Виконати дії :

    а)                                    г)

    б)                                       д)

    в)1-

 

 V. Тестування.

 

1. У дробі 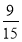знаменником є:

а) 9               б) 15                в) 24                      г)

 

     2. Який із написаних дробів є неправильним?

а)              б)                  в)                        г)

 

      3. На 3 і 5 ділиться число:

а) 205           б) 710              в) 925                     г) 405

 

      4. Яка з нерівностей є правильною:

а) >          б) <         в) <                  г) <

 

      5. =

а)                  б)              в) 2                          г)

 

      6. ++=

а)                б)             в)                       г)

 

      7. - =

а)                 б)             в) 1                      г) 1

 

      8. =

а)                   б)             в) 1                      г)

 

      9. 2=

а)                   б) 1           в) 2                   г)

 

     10. :=

а)                   б) 13           в) 6                       г)

 

 

      11.6:2=

а) 3                   б) 6             в) 3                   г) 3

 

      12.Якщо 5 : х = , то х дорівнює:

а) 6                       б) 294              в) 4                г) 60

Клас розбиваємо на групи:

1-а група: фахівці (перевірка виконання тестових завдань) ;

2-а група: філологи (завдання « Чи правильно ми говоримо?»);

3-я група: веселуни ( веселі задачі) ;

4-а група: розумники ( розгадування кросворду) ;

5-а група: практики (розв’язування практичних задач) ;

6-а група: кодувальники (задачі клоуна).

 VI. Чи правильно ми говоримо?   

Прийшов тато з міста, дає сину медівника та й каже:

- На, Васильку, та поділися з Петриком по щирості!

- А як діляться по щирості? – запитує Василько.

- Отак, сину, - каже тато, - більшу половину даси Петрику, а меншу – візьмеш собі.

- То дайте Петрику медівника, нехай він ділиться по щирості.

Чи правильно тут використовується термін «половина»?

Чи може бути одна половина меншою, а друга – більшою?

Слід говорити: більша частина, менша частина, оскільки половини мають бути однаковими. Адже дріб означає половину.

 

Назвіть дроби, які дорівнюють .

 

 .

   VII. Веселі задачі

1.Скільки буде, якщо ми цілий пиріг поділимо на 2 частини?

• на 4 частини?
• на 8 частин?
• На 16 частин?

На 64 частини? (Або крихти).

 

2.У мами дві доньки й один синок. Донечці пиріжечок, другій теж пиріжечок. А синочку? Ой, забула? Хай кожна сестриця дасть братові половинку. Так і зробили. То кому краще?

 

3.Великий російський письменник Л. М. Толстой писав, що  людину можна оцінювати дробом, знаменник якого складає те хороше, що вона думає про себе сама, а чисельник – те хороше, що думають про неї інші! Як ви вважаєте, чи правильно це?

(Учні висловлюють свою думку.)

 

VІІІ. Кросворд (ключове слово виділене – Буняковський)

    1.Закінчити речення:

«Числа ;  ;  ;    називають….

2. Одиниця вимірювання кутів.

3. Найменше натуральне число.

4. Дробову риску можна розуміти, як знак…

5. Ділення чисельника і знаменника дробу на їх спільний дільник.

6. Результат множення.

7. Дріб, у якому чисельник менший від знаменника.

8. Число записане над рискою дробу.

9. Знаменник, до якого зводять дроби при додаванні з різними знаменниками.

10. Компонент дії додавання.

12. Відстань між кінцями відрізку.

13. Закон множення для трьох множників.

  Розповідь вчителя.

  Віктор Буняковський один з провідних математиків 30 – 50 років 19 століття народився 3 грудня 1804 року в містечку Бар Подільської губернії. У 1921 році Віктор опинився у Парижі. В Сорбоні і в коледжі Буняковський вивчив математику під керівництвом Лапласа, Пуассона, Фур’є, Ампера та ін. Але найбільше він займався математикою у Коші. Буняковський зробив численні відкриття в теорії ймовірностей, з якою ми познайомимся при  вивченні наступної теми.

 

IХ Задачі клоуна.

 Через два дні до нас у місто приїжджають артисти цирку. Ви, мабуть, хочете дізнатись трохи про гостей, які незабаром завітають до нас. Вони прислали розповідь про себе, але її треба розшифрувати.

   Я веселий клоун . Мій зріст ( назви його в метрах). Мій друг важить  годинах).А після вистави ви зможете з’їсти у кафе морозива (назви у кілограмах). Ми продали 576 білетів, що становить усіх білетів. Скільки всього білетів ми продали?

 

Х. Розв’язування практичних задач.

1. Галина Василівна залишила дітям на столі сливи. Прокинувся Микола, з’їв 9 слив, що становить усіх слив. Потім Володя з’їв того, що було, а Катя - того, що залишилося. Скільки слив на тарілці залишилось?

2.Відстань від дому до школи 1км 300м . 1км Василь пройшов за од. До дзвінка залишилось 8 хвилин . Чи встигне дійти до школи Василь з тією самою швидкістю?

3. Маса слона 5т. Маса миші – 50г. Отже , миша більша від слона у 50:5 =10 разів? Яку частину становить маса миші від маси слона ?

4. Назвати дроби менші за .

5. Чи можна назвати найбільший дріб ?

 

ХІ. Оцінювання учнів.

 

ХІІ. Підсумок уроку.

 У давнину дії зі звичайними дробами викликали великі труднощі. Вавілоняни пояснювали це «втручанням злих духів». Англійський чернець Бєда , який був досить освідченню людиною свого часу, писав:»У світі є багато речей , але немає нічого важчого, як чотири дії арифметики.». Тоді ж , мабуть виникло німецьке прислів’я :«Потрапити у дроби», що означало – опинитися у скрутному становищі. А причина цих труднощів, полягала в тому, що не було відповідної теорії.

  Я думаю ,що ви не потрапите в скрутне становище через дроби, оскільки вмієте виконувати дії над ними, і ваші знання з кожним роком будуть поповнюватися. Спасибі вам за урок, ви гарно на ньому попрацювали.