Питання для самоконтролю та опорні конспекти з «Технічної механіки» («Теоретична механіка») для студентів ІІ та ІІІ курсу

Дана методична розробка є розробкою «Питання для самоконтролю та опорні конспекти з технічної механіки». Метою її написання є надання можливості студентам більш цілеспрямовано і ефективно працювати самостійно з літературою по  вивченню основних тем розділу «Теоретична механіка».

Методична розробка включає:

• питання для самоконтролю;
• опорні конспекти;
• перелік літератури, які можна використати для підготовки з вказаними параграфами і сторінками.

Питання для самоконтролю і опорні конспекти відповідають таким тематичним контролям:

1. Вступ. Основні поняття та аксіоми статики.
2. Плоска система збіжних сил.
3. Плоска система довільно розміщених сил.
4. Просторова система сил.
5. Центр ваги тіла.
6. Кінематика.
7. Динаміка.

 

 

 

 

 

 

 

 

 

Література

1. Ердеді О. О., Анікін І. В. Технічна механіка. – М.: В. школа, 1983.
2. Павловський М. А. Теоретична механіка. – К.: Техніка, 2004.
3. Бялер І. Я., Левінсон В. Н. Технічна механіка. – К.: В. школа, 1971.
4. Пастушенко С. І., Руденко О.Г. Практикум з теоретичної механіки частина І. – В.: Нова книга, 2006.
5. Пастушенко С. І., Руденко О.Г. Практикум з теоретичної механіки частина ІІ. – В.: Нова книга, 2007.

 

 

 

 

 

 

 

 

 

Тематичний контроль № 1

Вступ. Основні поняття та аксіоми статики.

 

1. Зміст предмету «Теоретична механіка». 
2. Роль і значення механіки  в техніці.
3. Механічний рух.
4. Рівновага. Абсолютно тверде тіло.
5. Матеріальна точка.
6. Сила та  її  характеристики. 
7. Система  сил.  Еквівалентні  сили.  Рівнодійна  і зрівноважувальні сили.
8. Аксіоми статики.
9. Вільне і невільне тіло.
10. В’язі та їх реакції. Основні види в’язей та їх реакції.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Література:   / 1 / стр.5 – 18.

   / 2 / стр. 5 – 13.

   / 3 /  стр. 5 – 8.

   / 4 /  стр.13 – 17.

 

 

 

 

 

 

 

 

 

Вступ. Основні поняття та аксіоми статики.

 

Література:   / 1 / стр.5 – 18.

   / 2 / стр. 5 – 13.

   / 3 /  стр. 5 – 8.

   / 4 /  стр.13 – 17.

 

 Механікою називається наука про механічний рух або  рівновагу матеріальних тіл  і виникаючу при  цьому взаємодію між ними.  Відноситься

механіка до природничих наук. 

 Теоретична механіка – це частина механіки, в якій вивчаються

найзагальніші закони механічного руху або рівноваги матеріальних тіл і механічної взаємодії між ними.

 Механічний рух – найпростіша форма руху матерії, яка зводиться до простого переміщення за часом фізичних тіл з одного положення в просторі в інше. 

 Матеріальною точкою  називається  тіло,  розмірами  якого  можна  знехтувати  при  розв'язанні  певних  задач. 

 Абсолютно  твердим  називається  тіло,  відстань  між  будь-якими точками якого не змінюється під час рівноваги або руху.  

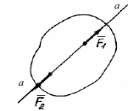
 Сила – фізична величина, яка є кількісною мірою механічної взаємодії між матеріальними тілами. Сила – величина векторна, її дія на абсолютно  тверде  тіло  визначається:  значенням  або  модулем  сили;  напрямом  дії сили;  точкою,  в  якій  вона  прикладена.  Пряма  аа,  уздовж  якої

спрямована сила, називається лінією  дії сили. Основною  одиницею сили  є                       

1  ньютон  (Н).  Це  сила,  яка  масі  в  1  кг  надає  прискорення  в  1  м/с².

Графічно  сила  зображується  спрямованим  відрізком-вектором, довжина якого виражає у вибраному масштабі  величину  сили,  а  напрям  відрізка

відповідає  напряму  сили.  Силу  позначатимемо буквою  F , а її величину (модуль) як F. Сукупність сил, що діють на абсолютно тверде тіло, називатимемо системою сил  (F₁ ,..., F_n).

 Наведемо ще такі визначення:

1. Тіло, яке не взаємодіє з іншими тілами і якому з даного положення можна надати будь-яке переміщення у просторі, називається вільним.

2. Якщо одну систему сил (F₁ ,..., F_n), що діють на вільне тверде тіло, можна замінити іншою системою (P₁ ,..., P_m), не порушуючи при цьому стану спокою чи руху, в якому знаходиться тіло, то такі дві системи сил називаються еквівалентними: (F₁ ,..., F_n)~ (P₁ ,..., P_m).

3. Система сил (F₁ ,..., F_n), під дією якої вільне тверде тіло знаходиться  у  стані спокою, називається  зрівноваженою, або еквівалентною  нулю:                   (F₁ ,..., F_n)~ 0.

4. Якщо задана система сил (P₁ ,..., P_m), еквівалентна одній силі, то ця сила називається рівнодійною  R  заданої системи сил: (P₁ ,..., P_m), ~  R .

5. Сила, яка прикладена до тіла в точці, називається зосередженою.

 Точкою прикладання  сили називається та  матеріальна частка тіла, до  якої ця сила безпосередньо прикладена.

6. Сили, що діють на всі точки довжини, поверхні чи об'єму, називаються розподіленими.

 Величину  сили,  яка  припадає  на  одиницю  довжини,  площі  або об’єму, називають інтенсивністю. Звичайно розподілену силу позначають  буквою  q,  яка  має  розмірність  Н/м,  Н/м²,  Н/м³  відповідно.

7. Зовнішні сили – це сили, що діють на тіло або механічну систему з боку матеріальних точок або інших тіл, якi не входять в цю систему.

8. Внутрішні сили – це сили взаємодії між точками однієї механічної системи.

 Класифікація систем сил:

- система збіжних сил, плоска й просторова; 

- плоска система паралельних сил; 

- довільна плоска система сил;

- просторова система паралельних сил;

- довільна просторова система сил.

Аксіома статики
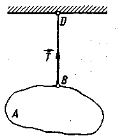
Вільне абсолютно тверде тіло може знаходитися під дією двох сил у рівновазі тоді й тільки тоді, коли ці сили рівні за модулем і діють уздовж однієї прямої у протилежних напрямах.
Дія заданої системи сил на абсолютно тверде тіло не порушується, якщо до неї додати або відняти зрівноважену систему сил.
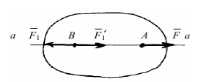
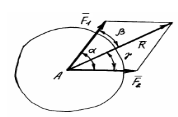
Система двох сил,  прикладених в одній точці до абсолютно твердого тіла, має рівнодійну, яка зображується діагоналлю паралелограма, побудованого на цих силах, і прикладена в тій самій точці.
Сили взаємодії двох матеріальних тіл і завжди рівні за величиною  і діють по одній прямій у протилежних напрямах.
Невільне  матеріальне  тіло  можна  розглядати  як  вільне, якщо  в’язі  замінити їх реакціями.

 

Види в’язей і їх реакції

 В'язями називають тіла або сукупність тіл, які обмежують рух даного тіла чи даної матеріальної системи.

Сила, з якою в'язь діє на тіло, щоб перешкодити будь-яким його переміщенням, називається реакцією в'язі.

 

Ідеально гладенька поверхня	Реакція – направлена по нормалі від поверхні
Нитка	Реакція – направлена вздовж нитки до точки її закріплення
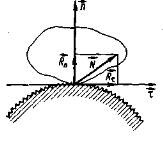
Шорстка поверхня	Реакція – розкладається на дві складові
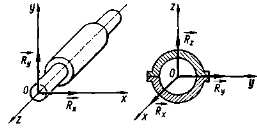
Шарніри: циліндричні і сферичні	Реакції – визначаються складовими по осях координат
Ідеальні стержні	Реакція – направлена вздовж осі стержня
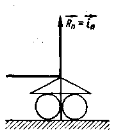
Котки	Реакція – направлена перпендикулярно до опорної площини котка

 

 

Тематичний контроль № 2

Плоска система збіжних сил.

 

1. Поняття  про  збіжні  сили  на  площинні. 
2. Додавання сил.
3. Силовий багатокутник.
4. Геометричний  засіб  визначення рівнодійної. 
5. Теорема про рівновагу тіла під дією трьох непаралельних сил.
6. Проекції  сил  і  рівнодійної  системи  сил  на  вісь.  Рівняння рівноваги.
7. Раціональний вибір координатних осей при рішенні задач.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Література:   / 1 / стр.19 – 24.

   / 2 / стр.19 – 21.

   / 3 /  стр. 11 – 14.

   / 4 / стр.19 – 28.

 

 

 

 

 

 

 

Плоска система збіжних сил.

 

Література/ 1 / стр.19 – 24.

   / 2 / стр.19 – 21.

   / 3 /  стр. 11 – 14.

   / 4 / стр.19 – 28.

 

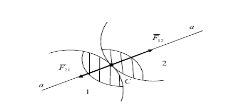
 Найпростішою  є  система  збіжних  сил,  тобто  система  сил,  лінії  дії яких перетинаються в одній точці (точці О збігу сил). Вона може бути просторовою чи плоскою. В останньому випадку всі лінії дії сил системи належать одній площині.

 

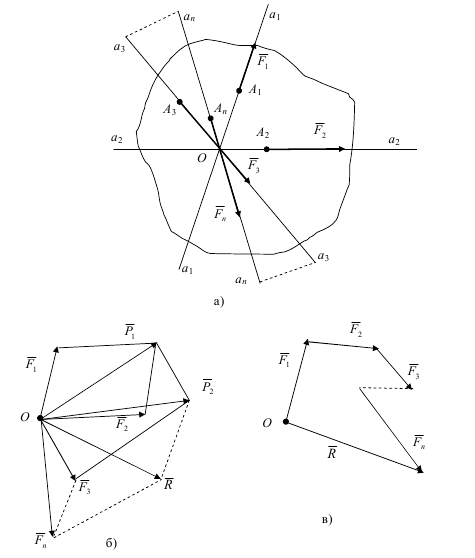
а)  система  збіжних  сил з лініями дії і точками прикладання;

б) перенесення сили  уздовж лінії дії  в точку О збігу;

в) знаходження рівнодіючої за правилом многокутника.

 

 

 

 

Умови рівноваги системи збіжних сил

Геометрична умова рівноваги	Для рівноваги системи збіжних сил необхідно і достатньо, щоб рівнодійна сила дорівнювала нулю.
Аналітична умова рівноваги	Для рівноваги  просторової  системи  збіжних  сил  необхідно  і  достатньо,  щоб суми проекцій цих сил на кожну з трьох координатних осей дорівнювали нулю.

 

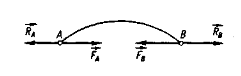
 Теорему про рівновагу трьох непаралельних сил застосовують  в тих випадках, коли треба знайти дві невідомі сили (реакції в’язів), які зрівноважують третю відому силу  (наприклад, силу  ваги тіла),  якщо відомо  точку прикладання однієї з невідомих сил і лінію дії іншої.

 Теорема. Якщо тіло перебуває в рівновазі під дією трьох непаралельних сил, з яких принаймні дві лежать в одній площині, то лінії дії всіх трьох сил перетинаються в одній точці, а вектори сил утворюють замкнений трикутник.

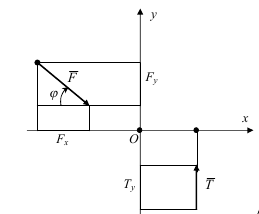
 Проекція сили на вісь – алгебраїчна величина, яка дорівнює довжині відрізка між проекціями початку і кінця сили на цю вісь. Проекція має знак “+”, якщо вектор сили нахилений у бік додатнього напрямку осі, і знак “-” –  якщо  в  бік  від’ємного  напрямку. 

Тому  буде

Тематичний контроль № 3

Плоска система довільно розміщених сил.

 

1. Плоска  система  довільно  розміщених  сил. 
2. Пара  сил  та  її характеристики.
3. Додавання пар, що  лежать  в одній площині.  Умова рівноваги пар. 
4. Момент сили відносно точки.
5. Зведення сили і системи сил до однієї точки.
6. Головний вектор  і  головний  момент  плоскої  системи  довільно

розміщених сил. Рівняння  рівноваги. 

7. Раціональний вибір  центра моментів  при розв’язуванні задач.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Література:   / 1 / стр.28 – 34, 34 – 39.

   / 2 / стр. 22 – 27, 28 – 32.

   / 3 / стр. 17 – 33.

   / 4 /  стр.29 – 36 .

 

 

 

 

 

 

 

 

Плоска система довільно розміщених сил.

 

Література:   / 1 / стр.28 – 34, 34 – 39.

   / 2 / стр. 22 – 27, 28 – 32.

   / 3 / стр. 17 – 33.

   / 4 /  стр.29 – 36 .

 

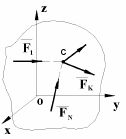
 Лема. Прикладену до тіла в точці О силу  F  можна перенести паралельно самій собі в будь-яку його іншу точку О₁ (центр приведення), додаючи при цьому, для збереження механічного стану тіла, пару сил ( F, F´), з моментом m_О1=m(F,F´), рівним моменту М_О1= (F),  вихідної сили  F  відносно центра приведення О₁.

а) до тіла прикладена розташована в площині  сила .

б) прикладено в площині у цьому центрі еквівалентну нулю систему  двох сил.

в) в центрі приведення побудовано вектор, рівний моменту отриманої пари

сил, і вектор, рівний моменту вихідної сили відносно полюса.

 Парою сил називається система двох, розташованих в одній площині паралельних сил, які рівні за величиною і протилежно направлені.

 Площина S, яка проходить через лінії дії сил пари, називається площиною дії пари. 

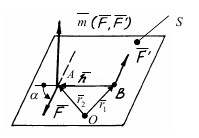
 Дія  пари  сил  на  тіло  призводить до його обертання навколо осі, яка перпендикулярна до площини дії пари сил.

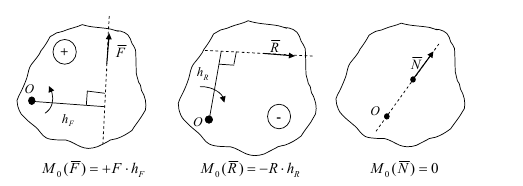
 Відповідно до механічної схеми на рис. 4.8 отримаємо наступні властивості моменту пари сил:

  -  за  величиною  момент  пари  сил  дорівнюватиме  модулю  вектора

m(F,F´):

 У цьому випадку h визначають плечем  пари сил (найкоротший відрізок між лініями дії сил, що складають пару);

- пара сил не має рівнодійної, тому що при  F=F´ виконується рівність  R= F +F´=0; при  цьому  властивості  сумісної механічної  (обертальної) дії сил пари на тіло зберігаються і проявляються у вигляді моменту m(F,F´)=hxF,   пари,  рівному  сумі  моментів  Мо(F) + Мо(F´) заданих сил  відносно  будь-якої  точки  О  тіла.

  Силовий фактор, під дією якого тіло може здійснювати обертальний рух, називається моментом сили відносно точки (полюса).

 З  математичної точки зору момент сили  F   відносно  точки  О визначається вектором M₀(F), який дорівнює векторному добутку радіуса-вектора r_A  точки А прикладання сили на її вектор  F :

 

 

 

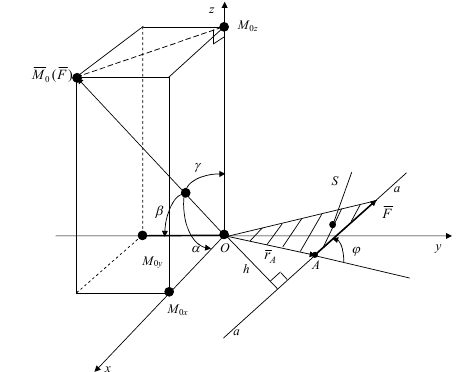
   а) додатній            б) від’ємний

 Для визначення алгебраїчного моменту сили відносно точки треба виконати такі дії:

  1) провести лінію дії сили;

  2) з вибраної точки опустити  перпендикуляр до лінії  дії  сили  (довжина   перпендикуляра h – плече сили);

  3) скласти добуток плеча на модуль сили;

  4) взяти знак “+”, якщо сила намагається повернути плече відносно

вибраної точки проти ходу стрілки годинника  і знак “-“ – за ходом стрілки годинника .

 Довільну  систему  сил,  що  діють  на тверде тіло, можна замінити еквівалентною системою, яка складається з  однієї  сили,  що  прикладена  в  довільно  обраному  центрі  зведення  і дорівнює головно вектору цієї системи сил, і  приєднаної пари  сил, момент якої  дорівнює головному  моменту  всіх сил відносно  обраного центра зведення.

----------------------------------------------

 

.

 

Умова рівноваги системи сил

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тематичний контроль № 4

Просторова система сил.

 

1. Сили в просторі, що сходяться в одній точці.
2. Рівняння рівноваги просторових збіжних сил.
3. Момент сили відносно осі. Момент пари, як вектор.
4. Приведення довільної просторової системи сил до сили та пари.
5. Рівняння рівноваги сил, довільно розташованих в просторі.
6. Рекомендації по методиці рішення задач на рівновагу просторової системи сил.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Література:   / 1 / стр.52 - 60.

   / 2 / стр.42 – 48. 

   / 3 /  стр. 42 – 45.

   / 4 /  стр.90 – 116 .

 

 

 

 

Просторова система сил.

 

Література:   / 1 / стр.52 - 60.

   / 2 / стр.42 – 48. 

   / 3 /  стр. 42 – 45.

   / 4 /  стр.90 – 116 .

 

Просторова система збіжних сил

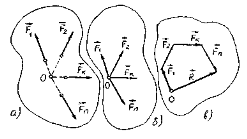
а)  дія сил у просторі, які перетинаються в одній точці,

б) зведення системи сил до рівнодійної,

в) побудова силового многокутника.

 

Довільно просторова система сил

 Відповідно до теореми Пуансо довільна система сил у просторі в загальному випадку  зводиться у  центрі  О до  двох силових факторів:  сили, яка дорівнює головному вектору F_о , і пари сил з моментом, який дорівнює

головному моменту M_о вихідної системи сил. Однак, на практиці між параметрами (величинами і взаємним напрямком) векторів F_о і M_о виникають різні співвідношення, що призводять до окремих випадків приведення довільної системи сил.

 Приведення  системи  сил  до пари  сил  (F,F´) з  моментом  m_O= OAх F. У цьому випадку в центрі приведення О головний вектор системи F_о=0, а головний момент  M_о= m_O  є перпендикулярним до пл. Е дії пари сил  (F,F´).

 

 

 

 

 

 

 

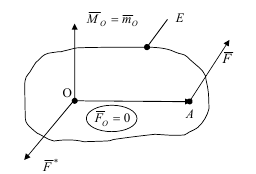
Рівновага системи сил у просторі

Просторова система збіжних сил	Аналітична  умова рівноваги	Для рівноваги збіжної системи сил у просторі необхідно і достатньо, щоб проекції рівнодійної на координатні осі цієї системи дорівнювали нулю.
Просторова система довільних сил	Геометрична умова рівноваги	Для рівноваги довільної системи сил у просторі необхідно і достатньо, щоб одночасно головний вектор і головний момент цієї системи дорівнювали нулю.
	Аналітична умова рівноваги	Для рівноваги довільної просторової системи сил, необхідно і достатньо, щоб алгебраїчні суми проекцій всіх сил на координатні осі були рівними нулю і алгебраїчні суми моментів всіх сил відносно  координатних осей також були рівними нулю.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 Тематичний контроль № 5

Центр ваги тіла.

 

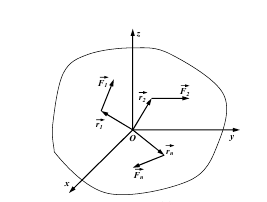
1. Поняття  про  центр  паралельних  сил. 
2. Формули  координат  центра  тяжіння твердого тіла.
3. Формули координат центра тяжіння об’єму, площі, статичний момент площі.
4. Формули координат центра тяжіння лінії.
5. Положення центра тяжіння простих геометричних фігур  і  перерізів
6. прокатних профілів.
7. Центр ваги  складних  плоских  фігур. 
8. Методи  визначення  центрів  тяжіння симетричних тіл.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Література:   / 1 / стр.61 – 65 .

   / 2 / стр.48 – 58.

   / 3 /  стр. 47 – 51.

   / 4 / стр.132 – 139 .

 

 

 

 

 

 

 

 

Центр ваги тіла.

 

Література/ 1 / стр.61 – 65 .

   / 2 / стр.48 – 58.

   / 3 /  стр. 47 – 51.

   / 4 / стр.132 – 139 .

 

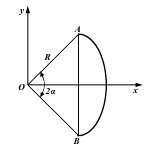
 Розглянемо дві паралельні сили F₁  і F₂ , направлені в один бік. Така  система  сил  зводиться до рівнодійної  R .  При цьому виконуються співвідношення:

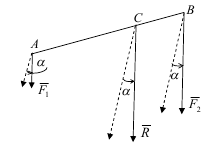
 Якщо сили F₁ і F₂ повернути на однаковий кут α навколо точок їх  прикладання А і В, то рівнодійна  R  повернеться на той самий кут навколо точки С,  оскільки  співвідношення  не  зміняться. Такі ж  міркування  можна привести і для двох паралельних сил, направлених у різні боки.

 Точка С, через яку проходить лінія дії рівнодійної системи паралельних сил при будь-яких поворотах цих сил навколо точок їх прикладання на однаковий кут, називається центром паралельних сил.

 У яких випадках існує така точка С і як знайти їх координати? На це запитання дає відповідь теорема про центр паралельних сил.

 Сили тяжіння окремих частин тіла до Землі направлені приблизно  до  його  центра.  Оскільки  розміри  тіл,  що розглядаються в задачах механіки, малі щодо радіуса Землі, то ці сили  умовно можна вважати паралельними. Рівнодійна цих паралельних  сил  є вагою  тіла,  а  центр  даної  системи паралельних  сил,  в  якому  прикладена  вага  тіла,  називається центром ваги тіла. Центр ваги твердого тіла займає положення, яке не залежить від орієнтації тіла у просторі.

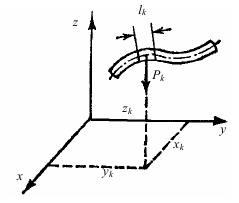
 Якщо  позначити  вагу  окремих  частин  тіла G_k ,  то координати  центра  ваги  визначаються  за такими формулами:

 

 

 

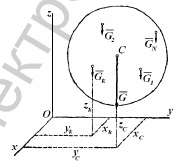
Центр ваги однорідного твердого тіла
Центр ваги однорідної пластини
Центр ваги однорідного стержня

 

Способи визначення координат центра ваги

 Спосіб  симетрії.  Якщо  однорідне  тіло  має  площину,  вісь  або центр  симетрії, то  його центр  ваги знаходиться  відповідно в  площині,  на осі або в центрі симетрії.

 

 Спосіб розбиття. Якщо тіло можна розбити на скінченне число таких часток, для яких положення центрів ваги відомі, то координати центра ваги тіла можна обчислити за формулами.

 

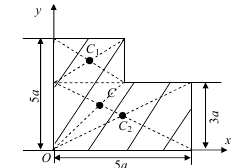
 Спосіб доповнення (або від’ємних площин). Якщо тіло має порожнину  (виріз),  то  цю  порожнину  (виріз)  можна  розглядати  як  тіло  з від’ємною вагою (площею) і для розрахунків використовувати спосіб розбиття.

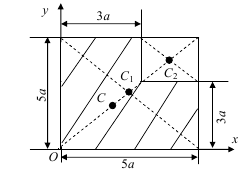
Центр ваги деяких фігур
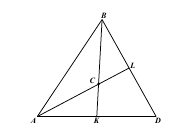
Центр ваги трикутника
Центр ваги дуги кола
Центр ваги колового сектора

 

Тематичний контроль № 6

Кінематика.

 

1. Кінематичні  рівняння  руху. 
2. Траєкторія,  шлях,  швидкість,  прискорення, кінематика обертального руху.
3. Класифікація рухів: прямолінійний рівномірний, прямолінійний

рівнозмінний.

4. Способи задання руху точки: координатний, натуральний.
5. Визначення швидкості, прискорення і шляху при всіх видах задання руху точки.
6. Нормальна, дотичне і повне прискорення.
7. Поступальний рух.
8. Обертальний рух твердого тіла навколо нерухомої осі.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Література:   / 1 / стр.69 – 110 .

   / 2 / стр. 62 – 147.

   / 3 /  стр. 53 – 84.

   / 4 / стр.154 – 177, 203 – 267, 325 – 355 .

 

 

 

 

 

 

Кінематика.

 

Література:   / 1 / стр.69 – 110 .

   / 2 / стр. 62 – 147.

   / 3 /  стр. 53 – 84.

   / 4 / стр.154 – 177, 203 – 267, 325 – 355 .

 

 Кінематикою  називається  розділ  теоретичної  механіки,  в  якому вивчається рух системи матеріальних точок з геометричної точки зору, зокрема  рух твердого  тіла  і матеріальної  точки  незалежно від  діючих на них сил.

  Вивчаючи рух тіла, завжди слід знати, відносно якого іншого тіла, що  називається  тілом  відліку, розглядається  цей рух.  Сукупність  тіла відліку,  з  яким  пов’язана  система  координат,  і  годинника  називають системою  відліку. 

Способи задання руху точки

 Натуральний спосіб. Якщо траєкторія точки відома наперед, то для визначення  закону  її  руху  в  просторі  достатньо  задати  положення точки  на  траєкторії.  Отже,  S  є  функцією часу:

 

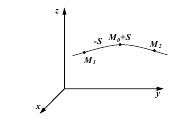
 Координатний спосіб. Цей спосіб визначення руху точки полягає в тому, що задаються координати точки як функції часу:

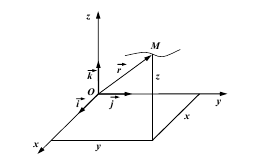
Швидкість руху точки

  Важливою  характеристикою  руху  точки  є  її  швидкість.  Нехай точка М  довільно  рухається  по деякій  кривій і в момент часу t займає положення  M₁,  а  через  досить  малий  проміжок  часу ∆t вона  займає положення.  Положення M визначається радіус-вектором r, а положення М₁ – радіусом- вектора  r+∆r. Тоді  Напрямок  вектора збігається  з  напрямком  вектора ∆r. Очевидно, що  середня швидкість лише наближено відображає характер дійсного руху точки. Щоб одержати швидкість у даний момент часу або у даній точці, слід перейти до границі. Отже,  швидкість точки  дорівнює першій  похідній радіуса-вектора точки за часом.

Одиниці вимірювання: м/с.

 

 

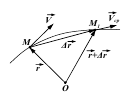
Прискорення матеріальної точки

 Якщо швидкість точки змінюється за величиною чи за напрямком, або за величиною і за напрямком, то для характеристики такого руху вводять поняття прискорення.

 Розглянемо загальний випадок зміни швидкості. Якщо в момент часу t₁  швидкість точки була v₁, а в момент часу t₂ вона стала , то величину:                          

називають середнім прискоренням точки за час.  Прискорення в будь-яку мить часу виражається (подібно миттєвій швидкості) рівнянням:

 Оскільки вектор dv₂ спрямований перпендикулярно до вектора v₂, то складову прискорення a_n називають нормальним прискоренням. Вектор a_n  паралельний dv₂, тобто спрямований по радіусу r до центра кривизни траєкторії. Нормальне прискорення визначає зміну швидкості за напрямом.

 

 Спрямована по дотичній до траєкторії, тому її називають тангенціальним прискоренням a_t. Тангенціальне прискорення визначає зміну швидкості за величиною.

Повне прискорення при криволінійному русі і його модуль дорівнюють:

.

Одиниці вимірювання: м/с².

 

 

 

Швидкість руху точки
Координатний спосіб
Напрям швидкості
Натуральний спосіб
Прискорення руху точки
Координатний спосіб
Напрям прискорення
Натуральний спосіб

 

 Рух  твердого  тіла,  закріпленого  в  одній  точці,  називається обертанням навколо нерухомої точки - центра обертання. Рух твердого тіла, при якому всі точки описують окружності, центри яких лежать на одній прямій, називається обертанням навколо нерухомої осі. Координатою в цьому випадку є кут повороту φ.

 

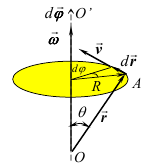
 Мірою переміщення матеріальної точки за малий проміжок часу служить вектор елементарного повороту, який направлений вздовж осі обертання.

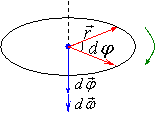
 Кутова швидкість матеріальної точки або тіла це фізична величина, яка визначається відношенням вектором елементарного повороту до тривалості цього повороту.

 Перша похідна за часом від кута повороту називається кутовою швидкістю:

Одиниці вимірювання: рад/с.

 Перша похідна від  кутової швидкості називається  кутовим прискоренням:

Одиниці вимірювання: рад/с².

 Знайдемо швидкість:

 У випадку, коли вісь обертання нерухома, вектор ε  паралельний вектору ω, і тому вектор [ε,r] спрямований убік швидкості v, тобто по дотичній до траєкторії , та являє собою тангенціальне прискорення:

 Нормальне прискорення:

 Модуль повного прискорення:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тематичний контроль № 7

Динаміка.

1. Основні закони динаміки.
2. Кількість руху, імпульс сили.
3. Робота, потужність.
4. Момент  інерції. 
5. Основний  закон  динаміки  обертального  руху. 
6. Робота  та потужність при обертальному русі.
7. Принцип Даламбера для матеріальної точки.
8. Принцип Даламбера для механічної системи.
9. Метод кінетостатики.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Література:   / 1 / стр.113 – 151 .

   / 2 / стр. 172 – 189, 219 – 240, 264 – 270, 271 – 297.

   / 3 /  стр. 87 – 117.

   / 5 /  стр.10 – 61, 102 – 109, 129 – 140, 189 – 218, 315 - 332.

 

 

 

 

 

 

Динаміка.

 

Література:   / 1 / стр.113 – 151 .

   / 2 / стр. 172 – 189, 219 – 240, 264 – 270, 271 – 297.

   / 3 /  стр. 87 – 117.

   / 5 /  стр.10 – 61, 102 – 109, 129 – 140, 189 – 218, 315 - 332.

 

 Динаміка вивчає зв'язок між взаємодіями тіл і виникаючими в результаті  цього  змінами  в  русі  взаємодіючих  тіл.

 Сила - це фізична величина, що визначає  зміну стану руху тіл,  і яка виникає  в результаті взаємодії тіл.

 Мірою  інертності  тіла  служить  величина, що  називається  масою  цього  тіла.

 Перший закон Ньютона. "Тіло перебуває в стані спокою або рухається рівномірно й прямолінійно, якщо рівнодійна всіх сил, що діють на тіло, дорівнює нулю”.

 Другий закон Ньютона.Прискорення,  що  надане  діючою  на  матеріальну  точку (тіло)  силою,  прямо  пропорційне  цій  силі,  збігається  з  нею  за напрямком й обернено пропорційне масі цього тіла.

 Третій закон Ньютона. Якщо тіло 1 діє на тіло 2 з деякою силою F₂₁, то й тіло 2, у свою чергу, буде діяти на тіло 1 з такою ж по величині й протилежно спрямованою силою F₁₂.

Кількість руху матеріальної точки є векторною величиною, яка є добутком маси на вектор її швидкості: Одиниці вимірювання: кгм/с.         Імпульс сили дорівнює добутку сили на проміжок часу її дії: Одиниці вимірювання: кгм/с. Механічна робота та потужність

 Механічна робота - це скалярна фізична величина, яка є мірою одної дії сили Р під час переміщення S точки її прикладання.

.

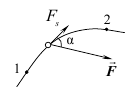
Одиниця роботи у системі СІ - Дж. Дж = Н·м.

 Потужність - скалярна фізична вели­чина, яка дорівнює відношенню роботи А до проміжку часу t, протягом якого вона була виконана:

Одиниця потужності у системі СІ - Вт. Вт = Дж/с.

 Робота сили тяжіння при вільному падінні з висоти:

 Робота,  виконувана  силою  пружності:

 Елементарна робота сили, яка прикладена до тіла, що обертається відносно осі, дорівнює моменту цієї сили відносно осі на елементарний кут повороту тіла:

 Потужність сили, яка прикладена до тіла, що обертається відносно нерухомої осі, дорівнює добутку моменту цієї сили відносно осі на кутову швидкість тіла:

 Швидкість зміни моменту імпульсу  тіла відносно нерухомої осі обертання дорівнює результуючому моменту відносно цієї ж осі всіх зовнішніх сил, що діють на тіло.

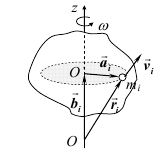
 Силою інерції матеріальної точки називають вектор, який дорівнює за модулем добутку маси точки на її прискорення і який спрямований протилежно вектору прискорення.

 

Принцип Даламбера
Для матеріальної точки	У будь який момент руху матеріальної точки активні сили і реакції в’язей зрівноважуються силою інерції, яка умовно прикладається до даної точки
Для механічної системи	У будь який момент часу головний вектор активних сил, головний вектор в’язей і головний вектор сил інерції складають зрівноважену систему сил

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рецензія

 

На методичну розробку по спеціальності  5.10010201 «Експлуатація та ремонт машин і обладнання агропромислового виробництва»  з дисципліни «Технічна механіка» при вивченні самоконтролю та опорних конспектів тем розділу «Теоретична механіка»  ВП НУБіП «Немішаївський агротехнічний коледж».

Методичну розробку підготовлено викладачем коледжу Лоїк О. А. з метою допомоги знань студентам, передбачених навчальним планом.

Методична розробка  з дисципліни «Технічна механіка» складено у відповідності з програмою для вищих навчальних закладів по підготовці молодших спеціалістів 5.10010201 «Експлуатація та ремонт машин і обладнання агропромислового виробництва» затвердженої начальником Департаменту кадрової політики, аграрної освіти і науки 24 грудня 2003р.

В методичній розробці охоплено весь матеріал тем розділу «Теоретична механіка», що дає змогу виявити у студентів знання, а також уміння і навички у межах затвердженої програми.

Методична розробка надає можливості студентам цілеспрямовано і ефективно працювати самостійно з літературою при вивченні основних тем розділу. Закріпити, розширити та поглибити знання матеріалу з технічної механіки. Це стосується питань статики, кінематики точки і твердого тіла, складного руху точки, динаміки абсолютного і відносного руху матеріальних точок, що дозволить перевірити і оцінити якість засвоєння теоретичного матеріалу.

Методична розробка базується на матеріалах, необхідних для забезпечення об’єктивного знання студентів.

 

 

 

 

 

 

Рецензент:

Голова циклової комісії

технічних дисциплін         Н. І. Мельченко

 

Викладач          О. А. Лоїк

 

 

 

 

 

 

 

 

Анотація

 

до методичної розробки з дисципліни «Технічна механіка»

для самоконтролю  знань студентів

 

Методична розробка відповідає вимогам навчальної програми, затвердженої навчально-методичним центром по підготовці молодших спеціалістів. Загальна кількість годин на дисципліну – 216 год.

Методична розробка дає можливість виявити рівень знань,  сформовані уміння студентів, закріпити, розширити та поглибити знання матеріалу з технічної механіки.

Методичну розробку розглянуто і затверджено на засіданні циклової комісії технічних дисциплін.

 

 

     Протокол № ___ від «____» _____ 20__ р.

     Голова циклової комісії

     ___________ Н. І. Мельченко

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВП НУБіП України «Немішаївський агротехнічний коледж»

 

 

 

Питання для самоконтролю

та опорні конспекти

з «Технічної механіки»

(«Теоретична механіка»)

для студентів ІІ курсу

 

     

          Виконала  викладач                    Лоїк О. А.

 

 

 

 

                                               

 

 

                     Розглянуто та схвалено на засіданні циклової комісії

                                                                                «Технічних дисциплін»

                                                                Протокол № ____ від _______20____р.

                                                                ___________________ Н. І. Мельченко