План-конспект уроку "Логарифмічна функція"
Тема уроку. Логарифмічна функція, її властивості і графік. слайд № 1
Мета уроку: слайд № 2
навчальна
- ввести поняття логарифмічної функції, дослідити її властивості, побудувати графік логарифмічної функції,
-
формувати вміння будувати графік логарифмічної функції
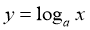 , застосовувати властивості логарифмічної функції при виконанні завдань, будувати графіки логарифмічної функції за допомогою перетворень графіку функції
, застосовувати властивості логарифмічної функції при виконанні завдань, будувати графіки логарифмічної функції за допомогою перетворень графіку функції 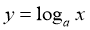 ;
;
розвиваюча
- розвивати логічне мислення;
виховна
- виховувати активність, самостійність, почуття відповідальності, культуру мовлення і математичних записів.
Тип уроку: засвоєння нових знань, формування вмінь.
Наочність та обладнання: комп’ютерна презентація.
Підручник:
А.Г. Мерзляк, Д.А. Номіровський В.Б., Полонський, М.С. Якір «Алгебра. 11 клас. Підручник для загальноосвітніх навчальних закладів. Академічний рівень, профільний рівень». – Х.: Гімназія, 2011.
Хід уроку
І. Організаційний момент
Привітання. Перевірка готовності учнів до уроку, налаштування на роботу.
ІІ. Актуалізація опорних знань
1. Повторити означення логарифма, властивості логарифмів слайд № 3
і формули логарифмування слайд № 4.
2. «Логарифмічна розминка» слайд № 5
(усно)
1. Обчислити:
1) log327 • log216 • log51
![]()
2) log2log2 3) lgtg10•lgtg20• lgtg30 • … • lgtg590• lgtg600
![]() 2. Чи мають вирази зміст ? а) log б) log3log3(1/3);
2. Чи мають вирази зміст ? а) log б) log3log3(1/3);
в) log3(-2)2.
(письмово)
Знайти значення виразу log32 • log43 • log54 • … • lg9.
Тестова робота слайд № 6
Обчислити:
|
|
1. 1) 28, 2) 13, 3) 75, 4) 30 2. 1) 0, 2) 1, 3) 4, 4) 8 3. 1) 7, 2) -1, 3) -2, 4) 1
4. 1) 45, 2) 49, 3) 47, 4) 5. 1) 3,5, 2) ln2, 3) ln124, 4) 32
6. 1)
|
Перевіримо відповіді
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
|
Номер правильної відповіді |
3 |
1 |
2 |
3 |
1 |
2 |
|
Правильна відповідь |
75 |
0 |
-1 |
47 |
3,5 |
10 |
Усно порівняти числа слайд № 7:
а) log232 і log264, б) log41/4 і log41/8 , в) log3(-1) і log3(-2),
г) log25 і log27, д) log0,31,7 і log0,31,9
Дані числа можна порівняти, користуючись властивостями показникової функції.
Але простіше це зробити за допомогою нової функції, з якою ми повинні ознайомитися на уроці.
Згадаємо:
З якою дією пов’язана поява логарифмів?
Які умови накладаються на основу а показникової функції?
Які властивості має показникові функція (за графіками при 0< a <1 і a > 1)? слайд №8
Чи існує функція, обернена до показникової? Чому?
ІІІ. Сприйняття й усвідомлення нового матеріалу
Оскільки показникова функція у = ах (a > 0, а ≠ 1) визначена на інтервалі (– ∞; + ∞) і строго монотонна на ньому, то за теоремою про існування оберненої функції існує функція, обернена до неї.
Функцію, обернену до показникової у = ах (a > 0, а ≠ 1), називають логарифмічною функцією з основою а і позначають
у = logax (a > 0, а ≠ 1). слайд №9
Оскільки графіки взаємно обернених функцій симетричні відносно прямої у = х, то, користуючись графіком показникової функції у= ах , можна побудувати графік логарифмічної функції у = logax. слайд № 10
Користуючись графіком, дослідимо властивості логарифмічної функції (записуємо в зошити).
1. Область визначення D(y) = (0; +∞). слайд № 11
2. Область значень Е(у) = (–∞; +∞). слайд № 12
3. Функція ні парна, ні непарна.
Знайдемо область визначення заданих функцій (усно): слайд № 13
у = loga (–x); у = loga (![]() ); у = loga (x–1);
); у = loga (x–1);
у = log0,1 x2; у = logх (x+3);
4. Нулі функції: у=0 при х=1. слайд № 14
Знайдемо нулі функцій (усно):
у = log3 (x+5); у = log5 (x–3); у = log1/4 x+2.
5. Проміжки знакосталості: слайди № 15-18
|
|
у > 0 |
у <0 |
|
a > 1 |
х1; |
х(0;1 |
|
0< a <1 |
х0;1 |
х1; |
З’ясуємо (усно) слайд № 19
20.7. Додатним чи від’ємним числом є:
|
1) |
2) |
3) |
4) |
20.18. Порівняйте:
|
1) |
2) |
6. Монотонність.
Якщо a > 1, то функція є зростаючою; слайд № 20
якщо 0< a <1, то функція є спадною. слайд № 21
Дослідити функції на монотонність (усно) слайд № 22
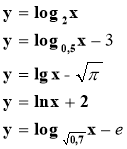
Повернемося до питання, яке ще не з’ясовано.
Порівняти: слайд № 23
log25 і log27, log0,31,7 і log0,31,9
Виконати усно. слайд № 24
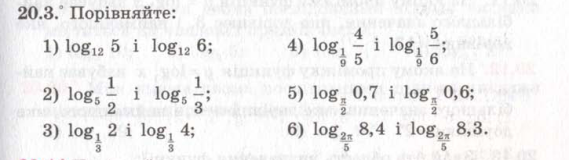

слайди № 25-26
7. Логарифмічна функція неперервна.
8. Логарифмічна функція диференційовна.
9. Пряма у=0 – вертикальна асимптота, коли х прямує до 0 справа.
10. Логарифмічна функція не має екстремумів та найбільшого і найменшого значень на всій області визначення.
слайд № 27

Графік логарифмічної функції. слайд № 28
Який з графіків є графіком функції у= log0,4х? слайд № 29
Побудуємо в зошитах графіки логарифмічних функцій: слайд № 30
у= log2х і у= log1/2х.
Згадаємо, як побудувати таких функцій (усно): слайд № 31
у= lg(х+2), у= │log1/2х│, у= lg(–х), у= – log3/2х.
№ 20.25. Нехай ![]() . Поясніть, за допомогою яких перетворень можна побудувати графіки функцій:
. Поясніть, за допомогою яких перетворень можна побудувати графіки функцій:
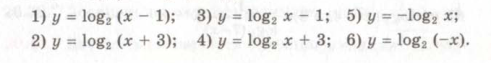
Використовуючи наявні графіки (*), побудувати
І варіант ІІ варіант
у=│log2х-2│ у= │log1/2(х+2)│
Трохи відпочинемо.
«Логарифмічна комедія» слайд № 32
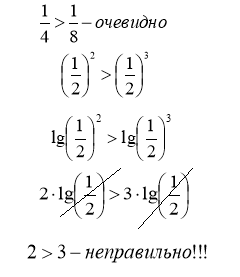
ІV. Формування вмінь застосовувати властивості логарифмічної функції при розв’язування завдань.
слайди № 33-34
![]()
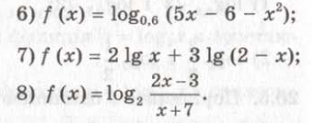
![]()
![]()
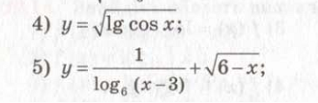
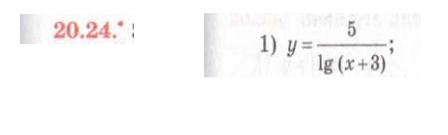
![]()

![]()
![]()
![]()

![]()
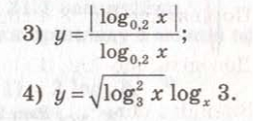
![]()
V. Підведення підсумків уроку.
Контрольні питання.
1. Яку функцію називають логарифмічною? Привести приклади.
2. Сформулювати властивості логарифмічної функції. слайди № 35-36
3. Коментар домашнього завдання.
VІ. Домашнє завдання.
П. 20 вивчити, №20.14, 20.22, 20.20, 20.29 слайд № 37
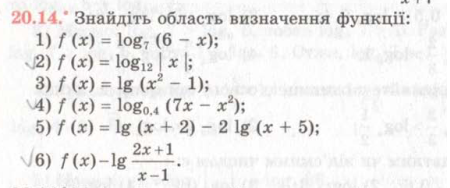


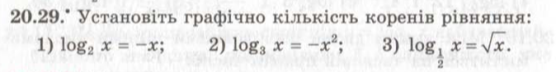


про публікацію авторської розробки
Додати розробку
