План-конспект уроку на тему "Відсоткові розрахунки", 10 клас

                                                        Урок 6

 

ТЕМА:  Відсоткові розрахунки

МЕТА :Узагальнити знання учнів, удосконалити вміння виконувати вправи та розв'язувати задачі, що передбачають відсоткові розрахунки. Розвивати логічні  мислення. Виховувати взаєморозуміння та повагу один за одного.

     Хід роботи

I. Перевірка домашнього завдання по готовим записам.

1.

2. Звільнитися від ірраціональності в знаменнику:

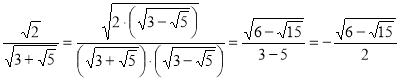
II.Актуалізація опорних знань

Математичний  диктант

 

1. Що називають відсотком?

2. Подайте у вигляді дробу (звичайного і десяткового)

2%;    20%;    50%;    63,5%;    75%;    100%;    135%;    250%

3. Подайте у вигляді відсотків

0,3;     0,04;      0,23;     ;    1,05;   ;    2,45

4. Що називається пропорцією? Наведіть приклади пропорцій.

5. Знайдіть невідомий член пропорції

а)    б)     в)      г) 

6. Що означає зменшення величини на 50%; на 10%; на 25%

7. Що означає збільшення величини на 100%;     на 200%;   на 300%

 

III. Перевірка математичного диктанту.

( Взаємоперевірка за відповідями викладача)

 

IV. Розв'язування задач.

     Викладач : ви знаєте, що існують 3 основні задачі на відсотки давайте їх повторимо

1) Знаходження відсотків від числа

2) Знаходження числа за його відсотками

3) Знаходження відсоткового відношення двох чисел

                 %

V. Розв'язування задач колективом

Основні задачі на відсотки:

1) Знаходження відсотка від числа: р% від числа а дорівнює: а %

2) Знаходження числа за його відсотком: якщо р % від числа х дорівнює b,  число дорівнює: х =  b : .

3) Знаходження відсоткового відношення двох чисел : число а становить . 100% від числа b.

Приклад 1.

Задачі  на знаходження відсотків від числа.

А) Скільки кілограм солі міститься в 50 кг 9 відсоткового розчину ?

    Розв'язання

50 кг ·% = 50 кг · 0,09 = 4, 5 кг.

Відповідь : 4,5 кг .

 

Б) Із 40 учнів дев'ятого класу 15 %  отримали річну оцінку з математики 12 балів. Скільки учнів отримало цю оцінку ?

40 % 40 · 0,15 = 6 (учнів)

Відповідь : 6 учнів.

В) Товар коштував 60 грн. Через деякий час його ціна знизилась на 40 %. Визначте нову ціну товару.

Визначимо, на скільки знизилася ціна товару:

60 грн. ·% = 60 грн. · 0,4 = 24 грн.

Тоді нова ціна товару:

60 грн. – 24 грн. = 36 грн.

Відповідь : 36 грн.

Приклад 2

Задачі  на знаходження числа та його відсотком.

А) Руда містить 8% олова. Скільки кілограм руди треба взяти, щоб отримати 96 кг олова?

     Розв'язання

96 кг :

Відповідь : 80 м ²

Б) Насос перекачав до басейну

 

48м³ : = = 80 м ³

Відповідь : 80 м ³

Ціну на товар знизили на 10 %, і він став коштувати 324. якою була початкова ціна товару?

Оскільки ціну на товар знизили на 10%, то 100% - 10 % = 90 % від початкової ціни вартість становить 324 грн. Отже, маємо :

324грн:

Відповідь : 360 грн.

Приклад 3

Задачі на знаходження відсоткового відношення двох чисел.

А) Знайдіть відсоток вмісту срібла в сплаві, якщо в 300 г сплаву міститься 63 г срібла.

    Розв'язання

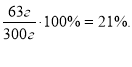
Відповідь :21%.

Б) Скільки відсотків години становлять 24 хв. ?

       Розв'язання

В одній годині 60 хв. Отже, маємо :

Відповідь:40%

 

 V. Робота з таблицею.

Відсотки

Відсоток – це сота частина деякого числа ( яке береться за одиницю ). 1% від числа
Знаходження відсотка від числа
р% від числа	Знайти 15% від 180. Розв’язання: Відповідь: 27.
Знаходження числа за його відсотком
Якщо р% від будь – якого числа дорівнює b, то все число дорівнює:	Знайти число, 22% якого дорівнює 33. Розв’язання. Шукане число – х – це розв’язок рівняння: Відповідь: 150.
Знаходження відсоткового відношення двох чисел
Число а складає від числа b	Скільки відсотків складає число 24 від числа 120 ? Розв’язання. Шукане число відсотків – х. Відповідь: 20%
Зміна числа, що виражена у відсотках
Число а збільшилось на р%: Число а зменшилось на р%:	Вартість товару а = 120 грн. збільшилась на 5%. Нова вартість товару: Відповідь: 126 грн.

 

 

 

VI. Самостійна  робота на 2 варіанта.

     Варіант 1

1. Вкладник поклав до банку 4000 грн. під 8% річних. Скільки грошей буде на

його рахунку через два роки?

2. Банк сплачує своїм вкладникам 6% річних. Скільки грошей треба покласти в банк, щоб через рік отримати 480 грн. прибутку?
3. Поклавши до банку 900 грн., через рік клієнт отримав відсотки, що становили 108 грн. Скільки відсотків річних сплачує цей банк?

Варіант 2

1. Вкладник поклав до банку 2000 грн. під 6% річних. Скільки грошей буде на його рахунку через два роки?
2. Банк сплачує своїм вкладникам 8% річних. Скільки грошей треба покласти в банк, щоб через рік отримати 600 грн. прибутку?
3. Поклавши до банку 1100 грн., через рік клієнт отримав відсотки, що становили 88 грн. Скільки відсотків річних сплачує цей банк?

Викладач збирає зошити на перевірку

VII. Підсумок уроку

VIII. Домашнє завдання

1) Руда містить 8% олова. Скільки грамів руди треба взяти, щоб отримати 96 кг олова??

2)Знайдіть відсоток вмісту срібла в сплаві, якщо 300 г сплаву міститься 63 г срібла.

3)Підприємець поклав у банк 50000гр. Під 10 % річних. Яка сума буде у нього на рахунку через 2 роки.