План уроку "Конус та його елементи"

 

ПЛАН УРОКУ

 

Дата «____»_________________ 202_ р.

Предмет: Геометрія

Тема: Тіла обертання

Тема уроку: Конус

Мета уроку:

 - сформувати в учнів поняття конуса та його елементів, а саме: твірної, осі, висоти, радіуса, діаметра; визначити види перерізів конуса; навчити учнів знаходити елементи конуса та визначати взаємне розміщення січної площини і конуса у просторі; застосовувати знання з теми для розв’язування задач;

- розвивати просторову уяву, індивідуальні здібності та пізнавальну активність учнів;

- виховувати творчу, працелюбну особистість шляхом навчання за допомогою швидкозмінних форм подачі інформації.

Тип уроку: урок вивчення нового матеріалу

Вид уроку: лекція  з елементами  пошукового практикуму.

Методи: словесні, наочні, частково пошукові, евристичні, практичні

Дидактичне забезпечення: «Робочий зошит з теми «Конус»», презентація викладача, моделі конуса

Обладнання: ноутбук, проектор, екран

Хід уроку

1. Організаційний момент.

Повідомлення теми і мети уроку. Для того, щоб дізнатися, над якою темою ми будемо працювати, нам необхідно розгадати наступний ребус

На партах для кожного учня приготовлено робочі зошити з теми «Конус».

2. Актуалізація опорних знань.

Учні працюють в підготовлених «Робочих зошитах».

(Проводиться у вигляді тесту з теми «Циліндр»).

1) Яка фігура є основою циліндра?

 а) Еліпс     б) Круг      в) Коло       г) Трикутник

2) Чому дорівнює площа основи циліндра з радіусом 2см?

 а) 4π     б) 8π        в) 4         г) 2π

3) Як називається відрізок, виділений білим кольором?

а) діагональ циліндра                              

б) апофема циліндра

в) твірна циліндра

г) висота циліндра

4) Чому дорівнює площа осьового перерізу циліндра,  радіус якого 1см  та твірна 3см?

      а) 6 см²

б) 3 см²

в) 6π см²

 г) 3π см²

 

 

5) Площа перерізу, утвореного січною площиною, перпендикулярною до осі циліндра, дорівнює 81π . Чому дорівнює радіус циліндра?

	А	Б	В	Г
1
2
3
4
5

 

а) 3 см

б) 9 см

в) 81 см

г) 6 см

 

 

(Правильність виконання завдання перевіряється з використанням методу взаємоперевірки).

 

 

 

III. Мотивація навчальної діяльності.

У навколишньому світі багато що пов’язує нас з геометрією. Існує чимало професій, представники яких не можуть обійтися без геометричної фігури, про яку ми сьогодні говоритимемо.  Слюсарі ,столяри, малярі, пожежники, геологи – усі вони мають справу з конусами, форми яких відтворюють також  природа, техніка та архітектура. 

 

   

 

   IV. Сприйняття й усвідомлення нового матеріалу.

Допоміжним засобом є презентація викладача, створена у програмі Power Point (ілюстративний матеріал до уроку, перевірка виконаних завдань).

Учні працюють в «Робочих зошитах», розроблених до уроку.

Пояснення і осмислення навчального матеріалу відбувається за допомогою інтерактивних методів: проводиться пошуковий практикум, знаходяться відповіді на проблемні питання, розв’язуються задачі-тести.

 

Лекція викладача з елементами проблемних питань та пошукового практикуму.

Назва цієї фігури пішла від грецького “конос”, так греки називали соснову шишку. А конус і справді схожий на неї.

Конусом називається тіло, яке складається з круга – основи конуса, точки, яка не лежить у площині цього круга – вершини конуса і всіх відрізків, що сполучають вершину конуса з точками основи. Відрізки, що сполучають вершину конуса з колом його основи – твірні конуса.

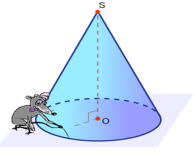
Конус називається прямим, якщо пряма, що сполучає вершину конуса з центром основи, перпендикулярна до площини основи.

 

 

Косий (похилий) конус – конус, у якого ортогональна проекція вершини не збігається з центром його основи.

 

 

 

 

 

 

 

 

 

 

 

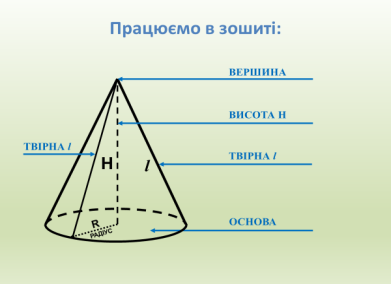
Теоретичні відомості

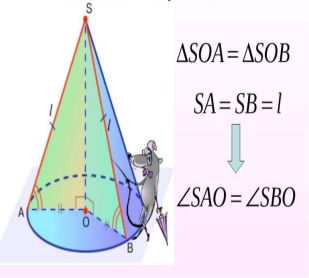
Всі твірні  конуса рівні між собою і складають рівні кути з основою.

                                          

 

 

 

 

 

 

 

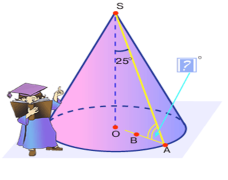?   Пошуковий практикум

 

Чому дорівнює  кут між твірною  і основою конуса, якщо  відомо  кут між висотою і твірною.

 

 

 

 

Теоретичні відомості

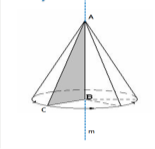Наочно прямий круговий конус можна розглядати як тіло, утворене в результаті обертання прямокутного трикутника навколо його катета як осі.

 

 

 

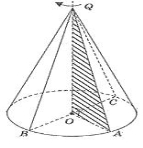
 Конус може бути отриманий шляхом обертання рівнобедреного трикутника навколо його висоти, опущеної на основу.

 

 

?     Проблемне питання у процесі осмислення нового матеріалу.

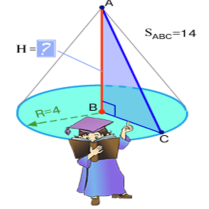Конус утворено при обертанні прямокутного трикутника S = 14 см2. Радіус основи конуса 4 см.

 Знайдіть висоту цього конуса.

 

 

 

 

Теоретичні відомості

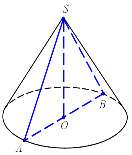Перерізи конуса площинами

Осьовий переріз конуса -це переріз, який проходить через вісь конуса.

ΔSAB – рівнобедрений.

SA=SB=l

AB=2R=d   

 

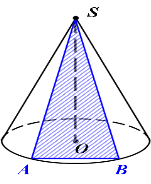
Переріз конуса площиною, яка проходить через його вершину, є рівнобедрений трикутник, у якого бічні сторони є твірними конуса.

 

 

? Пошуковий практикум

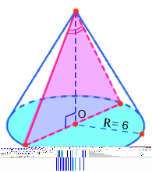Чому дорівнює площа осьового перерізу, якщо  радіус основи конуса дорівнює 6 см, а твірна  см?

 

 

 

Теоретичні відомості

Площина, паралельна площині основи конуса, перетинає конус по кругу, а бічну поверхню -  по колу з центром на осі конуса.

 

 

 

 

 

Задача-тест                                        

Через середину висоти конуса провели площину, яка перпендикулярна до осі конуса, та отримали круг r = 5 см. Чому дорівнює площа основи конуса?

А) 25 π;

Б) 10  π;

В) 100  π;

Г) 5 π;

Д) Інша відповідь.

 

 

Теоретичні відомості

 

? Пошуковий практикум (додатково)

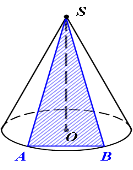1. Переріз конуса площиною, що проходить через вершину, перетинає його основу по хорді довжиною 6см, яку видно з вершини під кутом 60°. Знайти площу утвореного перерізу.

 

 

 

Задача

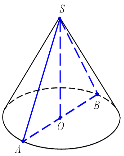2. Осьовий переріз конуса – прямокутний трикутник. Знайдіть площу цього перерізу, якщо радіус основи 5 см.

 

 

 

 

V. Осмислення нового матеріалу.

1. Розв’яжіть кросворд:

1.Фігура, утворена від обертання прямокутного трикутника навколо катета. (Конус).

2. Перпендикуляр, опущений з вершини конуса на площину основи. (Висота)

3. Відрізок, що сполучає вершину конуса з точкою кола. (Твірна)

4. Переріз, що проходить через вісь конуса. (Осьовий)

5. Вона сполучає вершину з центром прямого конуса. (Вісь)

6.Найвища точка конуса. (Вершина)

7 .Нижня частина конуса. (Основа)

					1
				2
		3
			4
						5
6

2 Виконайте тестове завдання:

 1. Конус – це тіло, утворене в результаті обертання…

А) Прямокутного трикутника навколо одного з катетів

Б) Прямокутного трикутника навколо гіпотенузи

В) Прямокутника навколо однієї з його сторін

Г)Трикутника навколо однієї зі сторін

Д) Правильного трикутника навколо однієї зі сторін

2. Якщо SB і SK – твірні конуса, то вони…

А) Мимобіжні

Б) Перпендикулярні

В) Паралельні

Г) Перетинаються

Д) Інша відповідь

3. Переріз конуса площиною, що проходить через його вершину є…

А) Кругом

Б) Півкругом

В) Рівнобедреним трикутником

Г) Прямокутником

Д) Рівностороннім трикутником

 4. Який переріз конуса, що проходить через його вершину, має найбільшу площу…

А) Круг

Б) Осьовий переріз

В) Рівнобедрений трикутник

Г) Прямокутний трикутник

Д) Рівносторонній трикутник

 

(Правильність виконання завдання перевіряється з використанням методу взаємоперевірки).

 

VI. Математичний вернісаж: «Конус навколо нас»

(перегляд презентації викладача).

Демонструються різні приклади використання зображень конусів, конусних  форм у природі та житті людей.

 

VII. Підбиття підсумків  уроку

• Роз’яснення незрозумілих питань.
• Самооцінювання робіт учнями.
• Оголошення оцінок за урок.

 

Твій настрій:

                                    

                       САМООЦІНКА:                ОЦІНКА ВИКЛАДАЧА:

 

VIII. Домашнє завдання.

1. Підручник під редакцією О. С. Істера «Математика: (алгебра і початки аналізу та геометрія, рівень стандарт)» для 11 класу, задачі №№ 6.4, 6.12, 6.17.
2. Творче завдання:  Напишіть реферат з елементами дослідження: «Конуси навколо нас чи ми навколо конусів».