Площа трикутника, заданого координатами своїх вершин

Площа трикутника, заданого координатами своїх вершин

Визначимо площу S трикутника А₁А₂А₃, якщо задані координати його вершин А₁(x₁;y₁), А₂(x₂;y₂), А₃(x₃;y₃).

 Будемо розглядати орієнтовані трикутники, тобто такі трикутники, відносно вершин якого зазначено, яка з них вважається першою, другою, третьою. Якщо через вершини трикутника А₁А₂А₃  будемо вважати додатною (від’ємною), коли рух по дузі кола А₁А₃, що містить вершину А₂, здійснюється в напрямку, протилежному напрямку руху (співпадає з напрямком руху)  кінця годинникової стрілки.

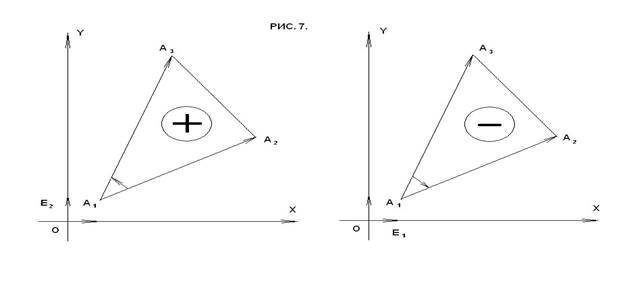
Розглянемо сторони трикутника А₁А₂ і А₁А₃ як вектори  

, де 𝑎 (а₁;а₂) і 𝑏⃗ (b₁;b₂). Знайдемо координати цих векторів: а₁=х₂-х₁;

b₁=x₃-x₁;                                                                                       а₂=y₂-y₁; b₂=y₃-y₁. 

Нехай  - кут від вектора a до вектора b , що співпадає з внутрішнім кутом трикутника. Тоді кут  > 0 у випадку додатної орієнтації трикутника і 

 0 в іншому випадку.

          За відомою формулою площа трикутника дорівнює : 

S   a  b sin,                                                        (*)

де a  a12 a22,b  b12 b22,sin aa21ba222 b1b12a2 b22 . 

1

Підставивши ці значення в  рівність (*), маємо:

S  12  a12 a22  b12 b22  a21ba222 b1b12a2 b22  12a1b2 b1a2, a1 

тобто S  x₂  x₁y₃  y₁x₃  x₁y₂  y₁, або

x1 y1 1

1 x2 x1 y2  y

S  x3 x1 y3  y1 x₂ y₂ 1

2

x3 y3 1

Якщо орієнтація трикутника А₁А₂А₃ додатна, то  > 0 і  S > 0; якщо ж

вона від’ємна, то   0 і  S  0.

ВПРАВИ:

№1. Обчислити площу трикутника, вершинами якого є точки: а) А(2;-3), В(3;2) і С(-2;5);

б) М₁(-3;2), М₂(5;-2), М₃(1;3);

в) М(3;-4), N(-2;3) і  P(4;5).

№2. Вершинами трикутника є точки А(3;6), В(-1;3),  С(2;-1). Обчислити довжину його висоти, що проведена з вершини С.

№3.  Визначити площу паралелограма, вершинами якого є точки А(-2;3), В(4;-

5) і С(-3;1).

№4. Вершинами паралелограма є точки А(3;7), В(2;3) і С(-1;4). Обчислити довжину його висот, що проведені з вершини В до вершин  паралелограма  АВСD.

№5.  Площа трикутника S=3, двома його вершинами є точки А(3;1) і В(1;-3), а третя вершина С лежить на осі Оу. Визначити координати вершини С.

№6. Площа трикутника S=4, двома його вершинами є точки А(2;1) і В(3;-2), а третя вершина С лежить на осі Ох. Визначити координати вершини С.

№7. Площа паралелограма S=12;  двома його вершинами є точки А(-1;3) і      В(-2;4). Знайдіть дві інші вершини цього паралелограма за умовою, що точка перетину його діагоналей лежить на осі абсцис.

№8. Площа паралелограма S=17;  двома його вершинами є точки А(2;1) і     В(5;-3). Знайдіть дві інші вершини цього паралелограма за умовою, що точка перетину його діагоналей лежить на осі ординат.