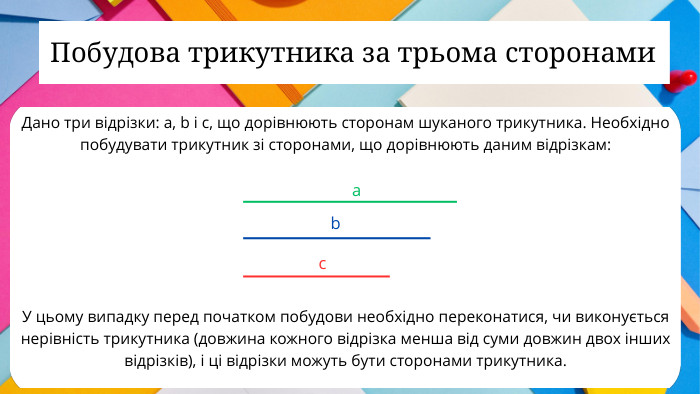
Побудова трикутника за трьома сторонами.

Побудова трикутника за трьома сторонами. Геометрія. 7 клас.

Центром кола, вписаного в трикутник, є точки перетину …Скільки кіл можна вписати в трикутник ?Коло, яке дотикається до всіх сторін трикутника, називається …В трикутник CDE вписано коло з центром в точці А. Знайдіть ∠E трикутника, якщо ∠ACD = 35°, а ∠E на 20° більший за ∠С. В трикутник CDE вписано коло з центром в точці А. Знайдіть ∠D трикутника, якщо ∠ACD = 25°, а ∠AED = 30°. Коло, вписане в рівнобедрений трикутник, ділить його бічну сторону на відрізки 5 см і 8 см, починаючи від основи. Знайдіть периметр трикутника. Згадаймо й знайдемо

1) усі побудови виконуються тільки за допомогою циркулята лінійки без поділок;2) за допомогою лінійки можна провести довільну пряму,провести пряму через задану точку,провести пряму, що проходить через дві дані точки;3) за допомогою циркуля можна провести коло (частину кола)довільного або заданого радіусаз довільним або заданим центромта відкласти від початку даного променя відрізок заданої довжини. При побудові фігур у геометрії домовилися дотримуватися таких правил:

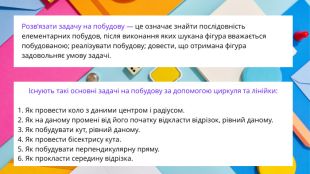
Розв’язати задачу на побудову — це означає знайти послідовність елементарних побудов, після виконання яких шукана фігура вважається побудованою; реалізувати побудову; довести, що отримана фігура задовольняє умову задачі.Існують такі основні задачі на побудову за допомогою циркуля та лінійки: 1. Як провести коло з даними центром і радіусом.2. Як на даному промені від його початку відкласти відрізок, рівний даному.3. Як побудувати кут, рівний даному.4. Як провести бісектрису кута.5. Як побудувати перпендикулярну пряму.6. Як прокласти середину відрізка.

Побудова трикутника за трьома сторонами. Дано три відрізки: a, b і c, що дорівнюють сторонам шуканого трикутника. Необхідно побудувати трикутник зі сторонами, що дорівнюють даним відрізкам: У цьому випадку перед початком побудови необхідно переконатися, чи виконується нерівність трикутника (довжина кожного відрізка менша від суми довжин двох інших відрізків), і ці відрізки можуть бути сторонами трикутника.аbc

Отже, побудуймо шуканий трикутник за допомогою циркуля і лінійки.1. За допомогою лінійки (нагадую, що лінійка без поділок) проводимо довільну пряму l.2. Позначаємо на ній точку В.3. Розхилом циркуля, що дорівнює довжині більшого відрізка a,описуємо коло з центром у точці В і радіусом a. Щоб не захаращувати малюнок, робимо тільки «засічку» з перетином прямої, тобто описуємо частину кола заданого радіусу.4. Нехай С — точка перетину цього кола з прямою l. Отже, ми відклали сторону а, що дорівнює ВС.5. Розхилом циркуля, що дорівнює довжині відрізка с, описуємо частину кола з центром у точці В.6. Розхилом циркуля, що дорівнює довжині відрізка b, описуємо частину кола з центром у точці C.7. Точка A — точка перетину цих кіл.8. Проведімо відрізок AC, з’єднуючи точки А і С за допомогою лінійки.9. Проведімо відрізок AB, з’єднуючи точки А і В за допомогою лінійки.10. Трикутник ABC має сторони, що дорівнюють a, b, c. Побудова

Доведімо, що побудований трикутник є шуканим. Для цього скористаймося ознаками рівності трикутників. За побудовою BC дорівнює a,BA дорівнює c,AC дорівнює b. Отже, побудований трикутник АВС є шуканим, за третьою ознакою рівності трикутників. Доведення

Завдання для самостійного опрацювання. Одна із сторін трикутника дорівнює 2,8 см, а друга - 0,6 см. Знайдіть тре тю сторону цього трикутника, якщо її довжина, виражена в сантиметрах, дорівнює цілому числу.​