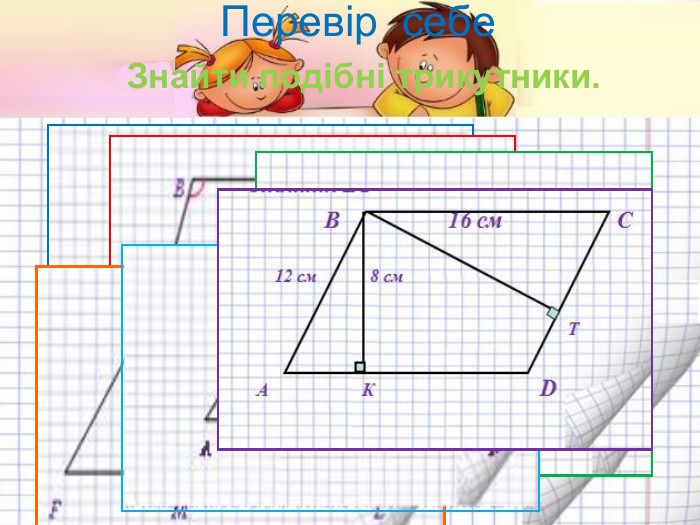
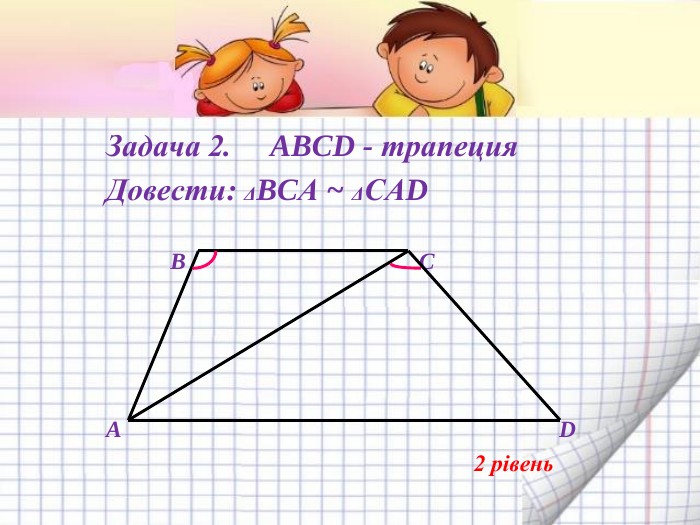
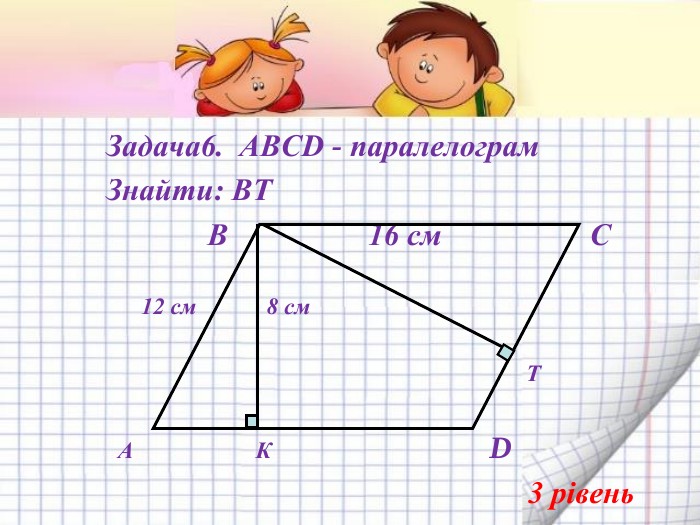
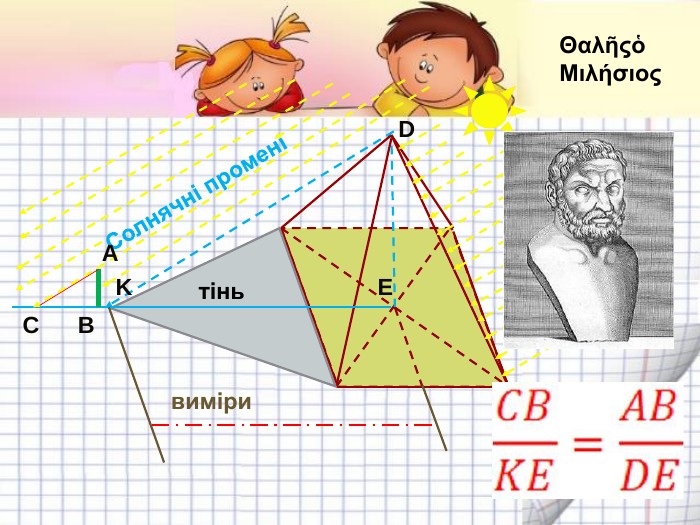
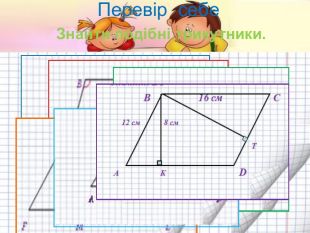
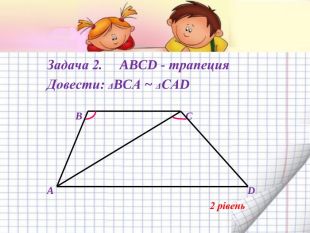
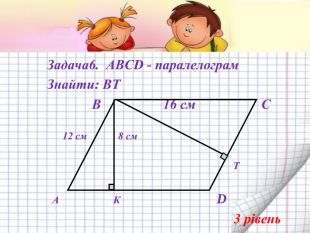
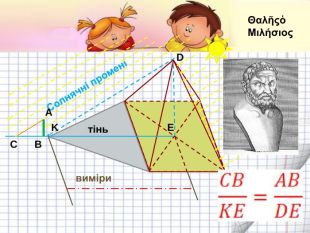
Подібність трикутників
Про матеріал
Урок - презентація з теми " Подібність трикутників". В ньому пропонуються різні види роботи для здобувачів освіти. Розглядаються задачі прикладного змісту, розв'язок яких націлений на розвиток критичного та логічного мислення. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Чудово. Дякую.


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку