Похідна функції. Частина 1

Математична скарбничка. Похідна функції та її застосування Частина 1. Півненко С.В.
Робочий зошит для учнів загальноосвітніх навчальних закладів та студентів закладів, що здійснюють загальноосвітню підготовку
Методична розробка включає приклади розвязання, основні теоретичні иатеріали необхідні для застосування навчок відшукання похідної.
Всі наведені матеріали – власна розробка автора. Завдяки наочним акцентам сприяє кращому розумінню та засвоєнню даної теми
Матеріал розташований на 14 сторінках
 ПОХІДНА ФУНКЦІЇ. ПРАВИЛА ОБЧИСЛЕННЯ ПОХІДНИХ.ТАБЛИЦЯ ПОХІДНИХ
ПОХІДНА ФУНКЦІЇ. ПРАВИЛА ОБЧИСЛЕННЯ ПОХІДНИХ.ТАБЛИЦЯ ПОХІДНИХ
𝑢 ![]() стала
стала
![]() 𝜗′
𝜗′
![]() 𝜗′
𝜗′
![]() 𝑢′
𝑢′
Степеневі Показникові Тригонометричні
𝑐′ 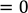
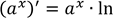 𝑎 (sin 𝑥)’ = cos x 𝑥′
𝑎 (sin 𝑥)’ = cos x 𝑥′ 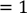
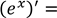 𝑒𝑥 (cos𝑥)’= - sin x
𝑒𝑥 (cos𝑥)’= - sin x
![]()
![]() Логарифмічні (𝑡𝑔 𝑥)′ =
Логарифмічні (𝑡𝑔 𝑥)′ = ![]()
𝑐𝑜𝑠![]() 𝑥
𝑥
![]()
![]()
![]()
![]() ′ = 1 (ctg 𝑥)′ = −
′ = 1 (ctg 𝑥)′ = −
𝑥 (ln𝑥)
𝑥 𝑠𝑖𝑛![]() 𝑥
𝑥
′ ![]()
![]()
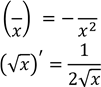
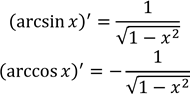 (log𝑎 𝑥)′ =
(log𝑎 𝑥)′ = ![]() Обернені тригонометричні x
Обернені тригонометричні x ![]() 𝑎
𝑎
(𝑎𝑟𝑐𝑡𝑔 𝑥)![]()
(𝑎𝑟𝑐𝑐𝑡𝑔 𝑥)![]()
Приклад 1![]() 𝟏
𝟏
![]()
![]()
![]() Знайти похідні:
Знайти похідні:
![]() ′
′
(𝑥4)′ = ________ (𝑥−3)′ = ________ ![]() ________
________
(𝑥12)′ = _______ (𝑥−12)′ = _______ ![]() ′ _______
′ _______
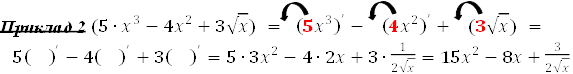 ′ ′
′ ′
![]()
Знайти похідні:
(4𝑥3 − 12𝑥2)′ =
5 ′
(6𝑥10 − 𝑥![]() 5) =
5) =
2 ′
![]() (6√𝑥 − ) =
(6√𝑥 − ) =
𝑥
(7𝑥
8 − 𝑥99)′ =
(3 𝑠𝑖𝑛 𝑥 − 2 𝑐𝑜𝑠 𝑥)′ =
′
(11𝑥![]() ) =
) =
(4 𝑎𝑟𝑐𝑠𝑖𝑛 𝑥 − 2 𝑎𝑟𝑐𝑐𝑜𝑠 𝑥 + 3𝑡𝑔 𝑥)′ =

Приклад 3
![]()
(𝑙𝑛 𝑥)′ = 𝟏![]() 𝒙 ; (𝑙𝑜𝑔𝑎 𝑥)′ = 𝑥
𝒙 ; (𝑙𝑜𝑔𝑎 𝑥)′ = 𝑥![]() 𝑙𝑛1 𝑎 ; (𝑙𝑜𝑔3 𝑥)′ = 𝑥
𝑙𝑛1 𝑎 ; (𝑙𝑜𝑔3 𝑥)′ = 𝑥![]() 𝑙𝑛
𝑙𝑛
![]()
![]() Обчислити похідні:
Обчислити похідні:
(3 ln 𝑥)′ =
(log2 𝑥)′ =
′
(log0,3 𝑥) =
(3 log2 𝑥 − 5 ln 𝑥)′ =

в) Похідна добутку та частки двох функцій
![]() 𝜗′
𝜗′
![]()
![]() 𝑢
𝑢
𝜗 𝜗
𝑢 = 3𝑥 + 5 𝜗 = 5𝑥2 − 1
𝑢’(𝑥) = 3 𝜗′(𝑥) = 10𝑥
′
![]() 𝝑′
𝝑′
![]()
![]() 𝟏𝟎𝒙
𝟏𝟎𝒙 ![]() 𝟏𝟓𝒙𝟐
𝟏𝟓𝒙𝟐 ![]() 𝟑𝟎𝒙𝟐 + 𝟓𝟎𝒙
𝟑𝟎𝒙𝟐 + 𝟓𝟎𝒙
![]() 𝟒𝟓𝒙𝟐
𝟒𝟓𝒙𝟐 ![]() 𝟓𝟎𝒙
𝟓𝟎𝒙 ![]() 𝟑
𝟑
![]()
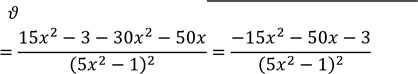 𝑢
𝑢 ![]()
![]()
![]() Обчислити похідні функцій:
Обчислити похідні функцій:
![]()
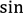 𝑥
𝑥 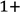 𝑥
𝑥
![]()
![]()
![]()
![]()
![]() 𝑥
𝑥![]() 𝑥
𝑥
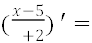 𝑥
𝑥
![]()
![]()
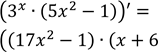
![]() (3𝑡𝑔 𝑥
(3𝑡𝑔 𝑥 ![]()
![]()
![]() Похідна складної функції
Похідна складної функції
′
![]() 𝜑′
𝜑′
|
|
|
Приклад 1 𝑦 ![]()
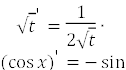
![]() 𝑦′
𝑦′ ![]() ′ [ 𝑡′ ]
′ [ 𝑡′ ] ![]()
![]()
𝑥
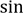 𝑥
𝑥
![]()
![]()
![]()
![]() ( мал.)
( мал.)
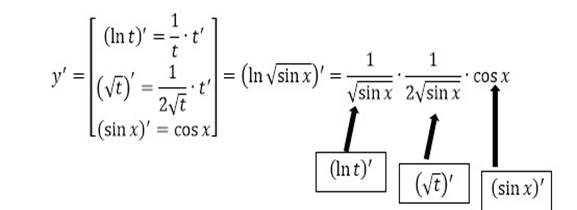
![]() Обчислити похідні заданих функцій:
Обчислити похідні заданих функцій:
𝑦 ![]()
𝑦′ ![]()
𝑦′ ![]()
![]()
𝑦′ ![]()
𝑦′ = (sin(18𝑥 − 3))′ = 𝑦′ = (ln5𝑥)′ = 𝑦′ = (sin(22𝑥 − 4))′ =
𝑥 ′
𝑦′ = (sin( − 3) =
2
𝑥 ′ 𝑦′ = (arcsin (4 − )) =
7
′
𝑦′ ![]()
![]() ′
′
𝑦′ = () =
Завдання 2
![]() Обчислити похідні складних функцій:
Обчислити похідні складних функцій:
𝑥2
1) 𝑦 = 𝑠𝑖𝑛 ![]()
1−𝑥
2) 𝑦 = cos(5𝑥3 − 6)
![]()
3) 𝑦 = 𝑙𝑛 √𝑡𝑔 𝑥
![]() 𝑥
𝑥
4)
𝑥
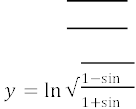 5) 𝑦 = √1−sin 𝑥 1+sin 𝑥
5) 𝑦 = √1−sin 𝑥 1+sin 𝑥
𝑥
6)
𝑥
![]() 1 7) 𝑦 = ln 𝑡𝑔 cos 32
1 7) 𝑦 = ln 𝑡𝑔 cos 32
√𝑥
8) 𝑦 = 𝑒𝑠𝑖𝑛 (5𝑥3−6𝑥2+3)
9) 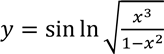
![]()


Завдання для роботи в групах (peer2peer)
High level (I)
Обчислити похідну функції:

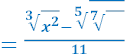 𝒙𝟑
𝒙𝟑
а)𝒚
![]() 𝒙 𝟑
𝒙 𝟑
𝟏𝟏𝒙𝟏𝟎−𝟔𝒙𝟓
б)𝒚 = ![]() 𝟏𝟐𝟏𝒙𝟏𝟐
𝟏𝟐𝟏𝒙𝟏𝟐
𝟒 𝐬𝐢𝐧 𝒙−𝟓 𝐜𝐨𝐬 𝒙
в)𝒚 = ![]()
𝐜𝐨𝐬 𝒙
г) 𝒚 = 𝟑𝒆𝒙(𝟏 − 𝒙𝟑)

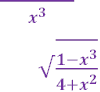 д) у
д) у ![]() 𝒔𝒊𝒏𝟑𝒙)
𝒔𝒊𝒏𝟑𝒙)
𝐥𝐧(𝟓𝒙−𝟏)
е) 𝒚 =
є) 𝒚 = 𝐬𝐢𝐧
ж) Розвязати рівняння: 𝒚′′ − 𝟑𝒚′ = 𝟎,
якщо 𝒚 = 𝟓𝒙𝟑 − 𝟔𝒙𝟐 + 𝟑
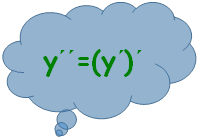

г) 𝒚 = 𝒙𝟑 ∙ 𝒔𝒊𝒏𝟐𝒙 
д) 𝒚 = (𝒙𝟓 − 𝒙𝟐) ∙ 𝐥𝐧 𝒙
 𝒙𝟐−𝟑
𝒙𝟐−𝟑
е) 𝒚 = 𝟒![]() +𝒙𝟐
+𝒙𝟐
𝑥3
є) 𝑦 = 𝑠𝑖𝑛 1![]() −𝑥2
−𝑥2
ж)Розв’язати рівняння 𝑦′ − 3𝑦 = 0, якщо 𝑦 = 5𝑥2 − 3𝑥
Low level (III)
Обчислити похідну функції:

![]() а) 𝒚 = 𝟓𝒙𝟐 − 𝟒𝒙𝟑 + 𝟑
а) 𝒚 = 𝟓𝒙𝟐 − 𝟒𝒙𝟑 + 𝟑
𝒙 𝟏
б) 𝒚 ![]()
𝒙
в) 𝒚 = 𝟏𝟏 𝐬𝐢𝐧 𝒙 + 𝟑
г) 𝒚 = 𝒙𝟒 ∙ 𝒆𝒙
д) 𝒚 ![]()
 е) 𝒚 =
е) 𝒚 = ![]()
𝟏+𝒙

𝒙
є) 𝒚 = 𝟓 𝐜𝐨𝐬 (![]() + 𝟑)
+ 𝟑)
𝟓
ж) Розв’язати рівняння 𝒚′ = 𝟎,
якщо 𝒚 = 𝟑𝒙𝟐 − 𝟏𝟔𝒙𝟑
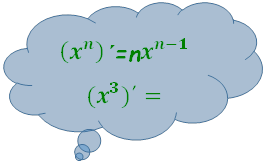
Super low level (IV)
Обчислити похідну функції:
 а) 𝒚 = 𝟑𝒙 − 𝟐𝒙𝟐
а) 𝒚 = 𝟑𝒙 − 𝟐𝒙𝟐
б) 𝒚 = 𝟑 𝐬𝐢𝐧 𝒙 − 𝟐
в) 𝒚 = 𝒙𝟏𝟎 − 𝟓𝒙𝟓 ![]()
г) 𝒚 = 𝒆𝒙 − 𝟓𝒙
 д) 𝒚 = 𝒆𝒙 ∙ 𝐬𝐢𝐧 𝒙
д) 𝒚 = 𝒆𝒙 ∙ 𝐬𝐢𝐧 𝒙
𝟒𝒙𝟐
 е) 𝒚 =
е) 𝒚 = ![]()
𝐜𝐨𝐬𝒙
 є) 𝒚 = 𝒆𝟓𝒙−𝟑
є) 𝒚 = 𝒆𝟓𝒙−𝟑
ж) Розв’язати рівняння 𝒚′ = 𝟎, якщо 𝒚 = 𝟓𝒙𝟐 − 𝟏𝟎𝒙


про публікацію авторської розробки
Додати розробку

