Показникова функція та її практичне застосування
«Показникова функція та її практичне застосування»
Урок систематизації та узагальнення знань учнів з теми «Показникова функція та її практичне застосування» може бути проведеним в кінці вивчення теми «Показникова функція», що дасть можливість систематизувати знання учнів означення та основних властивостей показникової функції, уміння застосовувати їх для розв’язання показникових рівнянь та нерівностей. Для цього учням пропонується розв’язання домашнього завдання на два варіанти, яке отримали учні на даний урок. При цьому, використовуючи метод аналогії, рівняння та нерівності, що розв’язуються одним способом, записані парами.
Під час актуалізації опорних знань перевіряються теоретичні знання з теми та вміння їх використовувати на початковому та середньому рівнях. Для цього пропонуються тестові завдання з вибором правильної відповіді та відкритої форми.
Домашнє завдання, яке отримують учні в кінці уроку, складене із завдань чотирьох рівнів. Виконання цих завдань підготує учнів до контрольної роботи, яка буде запропонована на наступному уроці.
Поставивши перед собою мету, ми провели дослідницьку роботу і виявили, що показникова функції має прикладне значення в наступних областях природничих наук: фізиці, хімії, біології, географії, астрономії, а також економіці банківської справи і виробництва.
Урок супроводжується двома презентаціями (учительською та учнівською).
Тема. Показникова функція та її практичне застосування
Мета:
навчальна: систематизувати, узагальнити знання учнів означення та основних властивостей показникової функції; уміння застосовувати їх до розв’язування показникових рівнянь і нерівностей, формувати початкові вміння моделювати реальні процеси за допомогою показникових функцій;
розвивальна: вдосконалювати навички застосовувати властивості показникової функції до розв’язування показникових рівнянь і нерівностей, розвивати творчу пошукову самостійність учнів з метою встановлення інтеграційних зв’язків математики з різними галузями наук та виробництвом, уміння працювати з додатковою літературою;
виховна: виховувати працьовитість, культуру математичної мови, вміння спілкуватися та висловлювати думку публічно.
Хід уроку
- Організаційний етап.
Привітання. Перевіряємо готовність учнів до уроку.
- Перевірка виконання домашнього завдання.
Учні перевіряють правильність виконання домашнього завдання на два варіанти за готовими розв’язками, які з’являються перед ними на моніторі комп’ютера з використанням методу аналогій. Під час перевірки коментують розв’язання, посилаючись на властивості показникової функції, методи розв’язання показникових рівнянь і нерівностей. Показникові рівняння і нерівності, що розв’язуються одним способом, записані парами.
1) Спосіб зведення рівняння (нерівності) до спільної основи.
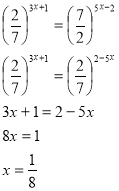

2) Метод винесення спільного множника за дужки.


3)Зведення до квадратного, методом введення допоміжної змінної.

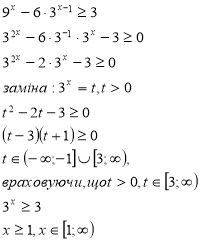
4) Однорідні показникові рівняння (нерівності).

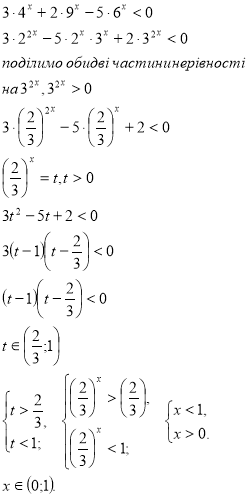
5) Рівняння, у яких основи спряжені ірраціональні вирази.

6) Нерівності виду ![]() або
або ![]()
![]()


- Мотивація навчальної діяльності, повідомлення мети і завдань.
В курсі математики ми отримуємо великий об’єм математичних знань. Інколи багато понять курсу алгебри та математичного анализу 10-11 класів носять абстрактний характер, і часто виникає запитання : «А де застосовуються ці знання, які ми отримуємо на уроках математики?» Так виникла ідея: дослідити, в яких областях науки, техніки знайшла застосування показникова функція. Поставивши перед собою мету, ми провели дослідницьку роботу і виявили, що показникова функції має прикладне значення в наступних областях природничих наук: фізиці, хімії, біології, географії, астрономії, а також економіці банківської справи і виробництва.

- Відтворення і корегування опорних знань, навичок і вмінь.
Фронтальне опитування та розв’язування тестових завдань.
- Яка функція називається показниковою?
- Які з наведених функцій є показниковими?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
- Серед наведених назвіть зростаючу та спадну функцію (пояснити свій вибір).
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
- Назвіть спільні властивості зростаючої і спадної показникової функцій.
-
Задано показникову функцію
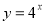 . Виберіть правильне твердження.
. Виберіть правильне твердження.
А. Графіком заданої функції є пряма.
Б. Задана функція спадає на всій області визначення.
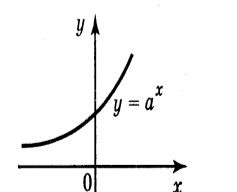
В. Графік заданої функції має вигляд:

Г. Графік заданої функції має вигляд:
- Використовуючи властивості показникових функцій, порівняйте числа:
а) 2-7 і 26 ; б) 1,73 і 1; в) ![]() ; г)
; г) ![]() .
.
- Знайдіть область визначення функцій:
а) y = 2x + 6; б) ![]() ; в) y = 3x + l; г)
; в) y = 3x + l; г) ![]() .
.
- Порівняйте числа х і у, якщо відомо, що правильна нерівність:
а) ![]() <
< ![]() ; б)
; б) ![]() <
< ![]() ; в) 3х <
; в) 3х < ![]() ; г)
; г) ![]() <
<![]() .
.
- Порівняйте основу a > 0 з одиницею, якщо відомо, що правильна нерівність:
а) а-2 > а2; б) аπ > а3; в) ![]() ; г)
; г) ![]() .
.
- Означення показникових рівнянь (нерівностей) та методи їх розв’язання.

- Сприймання й усвідомлення нового матеріалу.
-
Демонстрація учительської презентації з метою представлення навчального проекту. Ключове питання проекту: «Як застосовується показникові функція у природничих науках та економіці?».

В процесі реалізації проекту учні розглянули тематичні питання:
« Як застосовується показникова функція у банківських розрахунках?»
«Яким є застосування показникової функції у виробничих розрахунках?»
«Яким чином застосувується показникова функція у географії?»
«Як застосовується показникова функція в біології та хімії?»
«Яке застосування має показникова функції у фізиці та астрономії?
- Демонстрація однієї з учнівських робіт.
- Підсумки уроку. Рефлексія.
Які знання ви систематизували на уроці і що нового ви дізналися під час роботи над проектом?
Учитель повідомляє оцінки за дослідницьку діяльність учням, які попередньо представили результати своєї проектної діяльності.
- Домашнє завдання.
Початковий рівень
- Яка з даних функцій є показниковою?
|
А |
Б |
В |
Г |
|
|
|
|
|
- Яка з даних функцій є зростаючою?
|
А |
Б |
В |
Г |
|
у= |
у=10 |
|
|
-
Відомо, що

 . Порівняйте m і n.
. Порівняйте m і n.
|
А |
Б |
В |
Г |
|
mn |
mn |
m=n |
mn |
Середній рівень.
-
Графік функції
 перенесли паралельно на 2 одиниці вліво вздовж осі абсцис і на 6 одиниць вниз вздовж осі ординат. Графік якої функції було отримано?
перенесли паралельно на 2 одиниці вліво вздовж осі абсцис і на 6 одиниць вниз вздовж осі ординат. Графік якої функції було отримано?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Розв’яжіть рівняння
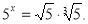
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Розв’яжіть рівняння

|
А |
Б |
В |
Г |
|
3 |
2 |
1 |
0 |
4. Розв’яжіть нерівність ![]()
![]() .
.
Достатній рівень.
-
Розв’яжіть нерівність
 .
.
-
Розв’яжіть рівняння
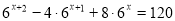 .
.
-
Розв’яжіть рівняння
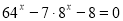 .
.
-
Розв’яжіть рівняння
 .
.
-
Розв’яжіть нерівність 5
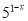 125.
125.
-
Розв’яжіть нерівність
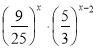
 .
.
Високий рівень.
1. Розв’яжіть рівняння ![]() .
.
2. Розв’яжіть рівняння ![]() .
.
3. Розв’яжіть нерівність ![]() .
.
4. Розв’яжіть нерівність ![]() .
.
Література
- А.Г.Мерзляк, Д.А.Номіровський, В.Б.Полонський, М.С.Якір
Алгебра, 11 клас: Підручник для загальноосвітніх навчальних закладів. Академічний рівень, профільний рівень. Харків, «Гімназія» 2011.
- Нелін Є.П. Алгебра і початки аналізу: Дворівневий підручник для 10 кл. загальноосвітніх навчальних закладів. Харків, «Світ дитинства», 2007
- Ясінський В.В. Математика: Навчальний посібник для слухачів ФДП НТУУ «КПІ», Київ 2005
1


про публікацію авторської розробки
Додати розробку
