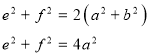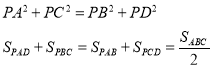Помічник з геометрії за власними розробками

1. Якщо у багатокутника п сторін, у нього  діагоналей.

                        D                                C

                                   K

                                                                B

      A

Якщо АК та ВК  – бісектриси,

то ;

                     c

           D                    C

       d                          b

               E         F

A                                  B

                    a

Якщо AE=EC i  DF=FB,

;

                        b

      B                                 C

  E

                    K   L                         

A                      a                     D            

              B                          C

                            O

       A                             H      P      <О=90°

       B                       C

                                              ; 

                                             CH- висота, <ACD=90°

A                               H   D                        

  В            b       C

                  О

h                                             ; <O=90°

A                   a                        D

          B                                C

       b       e              f

A            a           D                        для ромбу

B                                              C

      P

A                                              D

Якщо Р – будь-яка точка всередині ABCD,

То

Формула для знаходження площ трикутників, довжини сторін якого не є натуральними числами   

                  B 

A                          D                         C

Якщо BD – медіана,   то S_ABD= S_CBD

             B

A                         N                                                  C

Якщо BN – бісектриса, то   

Медіани трикутника – перетинаються в одній точці і поділяються нею у відношенні 2:1, рахуючи від вершини.

Точка перетину медіан трикутника називається центроїдом трикутника.

Довжини медіан трикутника визначаються через довжини його сторін за формулами:

m_a²= (2(b²+c²)-a²)

m_b²=  (2(a²+c²)-b²)

m_b²= (2(a²+b²)-c²)

m_a²+ m_b²+ m_b² = (a²+ b²+c²)

Бісектрисою трикутника називають відрізок бісектриси його кута, обмежений вершиною та протилежною стороною.

Точка перетину бісектрис трикутника називається інцентром і є центром кола, вписаного у трикутник.

                          В

                с

                     l_a          L_a

А                                   С

                   b

l_a²=bc - BL_a·CL_a

                     B

        D                                            E

A                                       F                               C

Якщо   DE,DF,EF –  середні лінії, то

S _ADF=S _BDE= S_DFE =S_EFC= S_ABC

                          B

             E             S₂          S₃               K

                 S₁                                                 S₄

A                             S₆             S₅                              C

                                          D

Якщо  BD, CE, AK – медіани,       S₁=S₂=S₃=S₄=S₅=S₆=

                               B

                                       y

               c    D

                                   x                  b

                                                E

A                                                    C

;

                    A

                K                    T

            L                                    S

                               P

B             N                                            M              C

Якщо AB //TN, AS //KM,  BC //KS,

           x  S₁   y                                                      

          x   S₂    y

         x    S₃       y

        x      S₄        y

       x       S₅           y

      x         S₆            y

     x           S₇             y

   x                               y

S₂: S₁=3:1; S₃: S₁=5:1; S₄: S₁=7:1

                           B

               D                       E

                          G

A                                           C

S_DGE=

                                                          C

         B

                                    ) ά

A                                                                 D

Якщо ABCD – довільний чотирикутник, то

;

                                                       C

               B

                                S₃

                  S₄                                  S₂

                              S₁

    A

                                                                       D

Якщо ABCD –  довільний чотирикутник, то

                              ;

      D              n             C

  p                                       p

A                    m                    B

Якщо ABCD –  рівнобока трапеція

(AD=CB=p,  AB=m, DC= n) ,

тоді

Висотою трикутника називається перпендикуляр, опущений з його вершини на пряму, якій належить протилежна сторона трикутника.

Точка перетину висот трикутника називається ортоцентром трикутника.

;