Шепетівська міська рада

Управління освіти виконавчого комітету

Методичний кабінет

 

 

 

 

 

 

 

ГЕОМЕТРИЧНІ НЕРІВНОСТІ

 

 

 

 

 

 

Кикоть В.М.,

Кислюк О.О.,

вчителі математики

НВК № 3 м. Шепетівки

 

 

 

 

 

2017

 

Кикоть В.М., Кислюк О.О.

 

 

 

 

 

 

ГЕОМЕТРИЧНІ НЕРІВНОСТІ

 

 

 

Посібник для підготовки учнів 7-11 класів до олімпіад

 

 

 

 

 

 

 

 

 

 

Шепетівка

2017

УДК 51

ББК 22.1я721

К-77

 

Автори:

В.М. Кикоть, вчитель-методист, вчитель вищої категорії, вчитель математики НВК № 3 м. Шепетівки

О.О. Кислюк, спеціаліст ІІ категорії, вчитель математики НВК №3 м. Шепетівки

 

 

 

 

К-77 Математика. Посібник для підготовки учнів 7-11 класів до олімпіад. Шепетівка, 2017. – 20с.

 

 

 

Матеріали упорядковані з метою надання допомоги з питань підготовки учнів до олімпіади у загальноосвітніх навчальних закладах (тема “Геометричні нерівності”).

Призначені для використання вчителями математики.

 

 

 

 

 

 

ББК 22.1я721

ISBN 978-966-07-0846-4

ЗМІСТ

 

ПЕРЕДМОВА

ГЕОМЕТРИЧНІ НЕРІВНОСТІ

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

ПЕРЕДМОВА

Незаперечною є істина, що для того, щоб навчитися розв’язувати задачі, треба їх розв’язувати. Але для надання більшої ефективності цьому заняттю потрібен певний теоретичний і практичний фундамент. Надто, коли мова йде про олімпіадні задачі.

Математична олімпіада – це інтелектуальне змагання високого рівня. Природно, що на ньому пропонуються завдання, нетрадиційні для повсякденної навчальної діяльності в школі.

Тема "Геометричні нерівності" є і почесною, і важкою. Не перерахувати олімпіадних і конкурсних завдань на цю тему. Та і, здавалося б, легкі, майже очевидні нерівності частенько виявляються "міцним горішком". Щоб учні не боялися цієї теми не обходили її стороною, дуже важливо правильно розставити акценти, зробити перші кроки! Не відштовхнути, не злякати, а надихнути!

Запропонований підбір задач є дуже доречним для учнів при їх першому знайомстві з геометричними нерівностями.

ГЕОМЕТРИЧНІ НЕРІВНОСТІ

Однією з перших нерівностей, з якою зустрічаємося при вивченні геометрії, є так звана нерівність трикутника. А саме: для будь-яких точок А, В, С площини АВ≤ВС+СА. У випадку, коли А, В, С є вершинами трикутника, нерівність стає строгою. Вже навіть така найпростіша властивість дає змогу розв’язувати змістовні задачі.

Задача 1. У трикутнику довжини двох сторін відповідно дорівнюють 3,14 та 0,67. Знайти довжину третьої сторони, якщо відомо, що вона виражається цілим числом.

Розв’язання. Якщо ця довжина дорівнює a, то a<3,14+0,67 та
a>3,14-0,67. А отже, a=3.

Задача 2. У площині взяли довільний трикутник ABC і коло радіуса 1. Довести, що на колі знайдеться точка, сума відстаней від якої до вершин трикутника не менша 3.

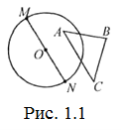
Розв’язання. Нехай М та N – дві діаметрально протилежні точки на колі (рис. 1.1).

Тоді MN=2. А отже, MA+AN≥2, MB+BN≥2, MC+CN≥2. Додавши ці нерівності,одержимо (MA+MB+MС)+(AN+BN+CN)≥6.

А тому, принаймні в одних дужках сума не менша від 3.

Розглянемо дещо складніший приклад застосування нерівності трикутника.

Задача 3. На сторонах трикутника ABC побудовано квадрати ВСКМ, BAQT, ACNP у зовнішній бік. Довести нерівності 5Р₁<2Р₂<6Р₁, де Р₁ – периметр трикутника ABC, Р₂ – периметр шестикутника MKNPQT.

Розв’язання.

Нехай BC=a, AC=b (Рис. 1.2).

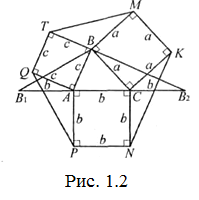
Очевидно, що P₂=P₁+KN+PQ+TM<P₁+(a+b)+(b+c)+(c+a)=3P.

Отже, 2Р₂<6Р₁. Для доведення нерівності 5Р₁<2Р₂ достатньо довести нерівність 3Р₁<2Р₂-2Р₁ тобто 3Р₁<2(KN+PQ+TM).

Для цього на прямій АС візьмемо точки В₁ та В₂ так, щоб АВ₁=СВ₂=b. Тоді ∆ВАВ₁=∆QAP, а ∆ВСВ₂=∆KCN (за двома сторонами та кутом між ними). Отже, BB₁=PQ, а ВВ₂=KN. Із трикутника В₁ВВ₂: ВВ₁+ВВ₂>В₁В₂, а значить, PQ+KN>3b. Аналогічно доводимо, що ТМ+PQ>3c, TM+KN>3а. Додавши останні три нерівності, одержуємо потрібну нерівність.

Нерівність трикутника може бути використана і для доведення ал­гебраїчних нерівностей. Наприклад.

Задача 4. Довести, що для додатних чисел а, b, с виконується нерів­ність .

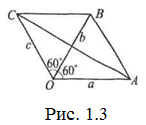
Розв’язання. Відкладемо відрізки ОА=а, ОВ=b, ОС=с так, щоб ˂AOB=˂BOC=60° (Рис. 1.3).

Тоді за теоремою косинусів

, , .

А отже, задана нерівність зводиться до очевидної: АВ+ВС≥АС.

Зі сторонами трикутника можуть бути пов’язані і дещо складніші нерівності. Наприклад.

Задача 5. Нехай а, b, с – сторони трикутника із периметром 1. Довести нерівність

Розв’язання. .

Аналогічно .

Отже, всі три дроби додатні. Нехай для визначеності а – найбільша із сторін трикутника. Тоді Оскільки на цьому проміжку
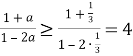– зростає, – спадає, то . Але ,
тому задана нерівність виконується.

Відзначимо, що можна одержати і більш точну оцінку:

Справді, зафіксуємо а і покладемо b=d+x, c=d-x. Розглянемо тепер різницю

Після нескладних спрощень одержимо, що вона дорівнює

.

Таким чином, найменше значення заданої суми досягається при b=с, якщо а – фіксоване. Зрозуміло, що при цьому а=b=с, бо інакше, зафіксувавши, наприклад, с. ми могли б зменшити суму, взявши а=b. А отже,

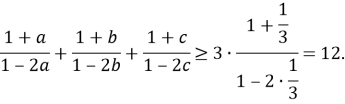
Крім сторін, у нерівностях можуть фігурувати також інші елементи трикутника чи інших фігур.

Задача 6. Довести, що в будь-якому трикутнику сума медіан т_а+m_b+т_с більша периметра, але менша периметра.

Розв’язання. Нехай для трикутника ABC точка D – симетрична до А відносно середини А₁ сторони АС (Рис. 1.4).

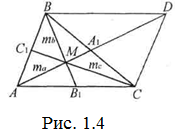
Тоді 2т_а=AD<AB+BD=AB+AC=b+c.

Аналогічно доводимо, що 2m_b<a+c, 2m_c<b+a. Додавши ці нерівності, одержимо m_a+m_b+m_c<a+b+c.

В іншу сторону, якщо М – точка перетину медіан, то АМ+ВМ>АВ, ВМ+СМ>ВС, АМ+СМ>АС.

Додаючи ці нерівності і враховуючи, що

, одержимо

звідки і випливає потрібна нерівність.

Задача 7. Довести нерівність де – бісектриса три­кутника AВС, проведена до основи а, р – його півпериметр.

Розв’язання. Нехай продовження бісектриси AD перетинає описане навколо трикутника ABC коло в точці М. Тоді AD·DM=CD·DB. Оскільки ∆ABD~∆AMC (за двома рівними відповідними кутами), то АВ·АС=AD·AM=AD(AD+DM)=AD²+BD·DC. Крім того, за властивістю бісектриси трикутника , звідки . Тоді

.

А отже, .

Задача 8. Всередині трикутника ABC розташований відрізок MN. Довести, що його довжина не перевищує найбільшої сторони трикутника.

Розв’язання. Нехай пряма MN, що проходить через внутрішні точки М, N трикутника ABC, перетинає сторони в точках М₁ та N₁, причому для визна­ченості візьмемо, що М₁ лежить на АВ, N₁ – на ВС (Рис. 1.5).

 

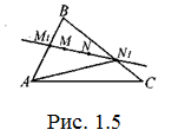
Зрозуміло, що MN≤M₁N₁. З двох кутів AM₁N₁ та BM₁N₁ принаймні один не  менший за 90⁰. А тому М₁N₁≤AN₁ або M₁N₁≤BN₁≤ВС. Аналогічно, з кутів BN₁A та CN₁A принаймні один не менший за 90°. Отже, AN₁≤AB або AN₁≤AC.

Таким чином, MN не перевищує довжини принаймні однієї, отже, і найбільшої сторони трикутника ABC.

Узагальнюючи задачу 8, приходимо до такого твердження: довжина відрізка всередині опуклого многокутника не перевищує довжини найбільшої сторони або найбільшої діагоналі цього многокутника.

Відзначимо також, що якщо всередині опуклого многокутника лежить інший опуклий многокутник, то периметр Р₂ зовнішнього многокутника не менший, ніж периметр Р₁внутрішнього.

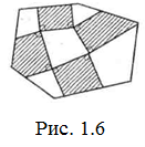
Справді, побудуємо на сторонах внутрішнього многокутника півсмуги, паралельні сторони яких перпендикулярні до відповідних сторін цього многокутника (Рис. 1.6). Якщо Р – та частина периметра зовнішнього многокутника, яка знаходиться всередині цих півсмуг, то, очевидно, справджуються нерівності Р₁ ≤Р₂ та Р₂Р₁.А тому Р₂≥Р_1.

Крім лінійних елементів у нерівності можуть входити кути та площі фігур. Зокрема, досить очевидним є твердження, що площа трикутника не перевищує півдобутку будь-яких двох його сторін:

.

Задача 9. Площа трикутника зі сторонами а<b<с дорівнює 1. Довести, що .

Розв’язання. Оскільки, то .

Задача 10. Довести, що площа трикутника, вершини якого лежать на сторонах паралелограма, не перевищує половини площі паралелограма.

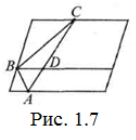
Розв’язання. Якщо дві вершини трикутника лежать на одній стороні паралелограма, то його основа і висота не перевищують відповідно сторони і висоти паралелограма (Рис. 1.7). Отже, твердження задачі в цьому випадку справедливе.

Якщо ж усі вершини трикутника лежать на різних сторонах паралелограма, то знайдуться дві вершини, наприклад А і С, які лежать на протилежних сторонах. Проведемо тоді через В пряму, паралельну основі паралелограма. В результаті трикутник ABC розіб’ється на два трикутники BCD та ABD, спільна основа BD яких лежить на одній стороні відповідних паралелограмів. Тому приходимо до вже розглянутого випадку.

Задача 11. У будь-який опуклий многокутник площі S можна помістити прямокутник, площа якого не перевищує 2S.

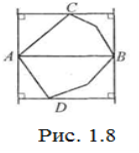
Розв’язання. Справді, нехай АВ найбільша діагональ чи сторона такого многокутника (Рис. 1.8).

Проведемо через А та В прямі, перпендикулярні до АВ і розглянемо перпендикулярні до них прямі, які мають із заданим многокутником лише одну спільну точку (відповідно точки С та D) або цілу сторону (наприклад АВ, якщо АВ – сторона многокутника; тоді точку С чи D візьмемо на цій стороні). Ці чотири прямі обмежують прямокутник, площа якого S₀=2S_∆АCB+2S_∆АDB<2S, де S – площа заданого опуклого многокутника.

Задача 12. Довести нерівність , де S— площа трикутника, р – його півпериметр.

Розв’язання. Із формули Герона маємо:

.

Тут ми скористалися відомою нерівністю Коші між середнім арифметичним і середнім геометричним кількох додатних чисел

. Звідси і випливає потрібна нерівність.

Відзначимо, що для доведення окремих нерівностей як допоміжний засіб може використовуватися площа. Наприклад.

Задача 13. Довести, що h_a+h_b+h_c≥9r, де h_a, h_b, h_c – висоти трикутника, а r – радіус вписаного в нього кола.

Розв’язання. Оскільки ah_a=2S=r(a+b+c), то Аналогічно знаходимо .

Звідси ,

бо для додатних чисел х, у завжди .

Що ж стосується нерівностей із кутами, то у більшості з них фігурують тригонометричні функції цих кутів. Тому такі нерівності доречніше розглядати у тригонометрії.

Задача 14. Доведіть, що в трикутнику проти більшої сторони лежить більший кут.

Доведення. Нехай b>с. Доведемо, що В>С (рис. 1.9).

 

 

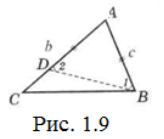
Відкладемо AD=c на стороні b. Тоді ˂1=˂2 і ˂1<B (складає частину кута В). ˂2>C (оскільки ˂2 – зовнішній для ∆BDC). Звідки, і ˂1>C, і тим більше В>С. Що й потрібно було довести.

Задача 15. Доведіть що проти більшого кута в трикутнику лежить більша сторона.

Доведення. Нехай В>С. Доведемо, що у такому випадку b>с. Припустимо протилежне: b<с. Але тоді, за попередньою задачею В˂С, що протирічить умові. Отже, наше припущення невірне, а тому b˃с.

Задача 16. Доведіть нерівність трикутника: кожна сторона менше суми двох інших сторін і більше їх різниці.

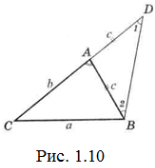
Доведення. Нехай а – найбільша сторона в трикутнику ABC (рис.1.10).

Доведемо, що а<b+с і а>b-с. На продовженні АС відкладемо AD=c.

Тоді (оскільки А – зовнішній кут для ∆BDA). ˂DBC> ˂2, тобто (оскільки ˂2 складає частину кута DBC).

У трикутнику BDC сторона а лежить проти кута , а сторона b+с – проти кута, більшого за .

Отже, а<b+с. Тим більше, с<а+b і b<а+с. Перенесемо в останній нерівності с в ліву частину, отримаємо: а>b-с. Що й потрібно було довести.

Задача 17. Точка К знаходиться усередині ∆АВС. Що більше: ˂BAC чи ˂BKC (рис.1.11)?

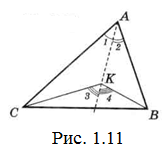
Розв’язання.

Проведемо пряму АК. Очевидно, що ˂3> ˂1 (він зовнішній для ∆АКС) і ˂4> ˂2 (зовнішній для ∆АКВ). Тоді і ˂BКC=˂3+˂4 буде більшим, ніж ˂BAC=˂1+˂2.

Задача 18. Яку сторону видно під найбільшим кутом:

a) з центру вписаного кола;

b) з центру описаного кола?

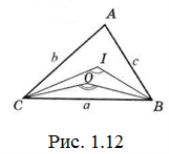
Розв’язання. Нехай в ∆АВС а˃b˃с (Рис. 1.12).

Тоді, за задачею 14, А˃В˃С. Оскільки , то він буде найбільшим із кутів ВІС, АІС, АІВ. Оскільки ˂ВОС=2А (як центральний кут), то він буде більшим серед кутів ВОС, АОС, АОВ. Таким чином, з центра вписаного і з центра описаного кіл під найбільшим кутом видно найбільшу сторону.

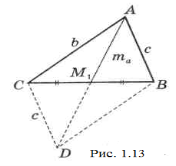
Задача 19. Доведіть, що медіана трикутника менша півсуми прилеглих до неї сторін.

Доведення. Згідно рисунка 1.13, доведемо, що .

Продовживши медіану вдвічі, отримаємо паралелограм ABDC.

І (за нерівністю трикутника для ∆АСD), що й потрібно було довести.

Задача 20. Доведіть, що для суми медіан будь-якого трикутника справедлива наступна подвійна нерівність: .

Доведення. Згідно із задачею 19, .

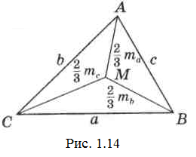
Додавши ліві і праві частини нерівності, отримаємо: . Далі для ∆АМВ (рис.1.14): .

Далі для ∆BМВ: і ∆CМВ: .

Додавши ліві і праві частини нерівностей, отримаємо:

.

Що й потрібно було довести.

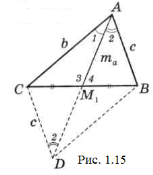
Задача 21. У ∆АВС (b>с) проведена медіана (рис. 1.15). Який з кутів більший ˂1 чи ˂2? ˂3 чи ˂4?

Розв’язання.

Продовживши медіану , отримаємо паралелограм ABDC, в якому CD=c і ˂ADC=˂2 (як внутрішні різносторонні). У трикутнику ACD проти сторони b лежить ˂2, а проти с – ˂1. Оскільки b>с, то ˂2> ˂1. крім того, ˂3=˂2+B (зовнішній для ∆АВМ₁), a ˂4=˂1+C (зовнішній кут для ∆ACM₁). Тоді очевидно, що ˂3> ˂4.

Задача 22. Доведіть, що відрізок між вершиною і протилежною стороною трикутника менший найбільшої з двох інших сторін.

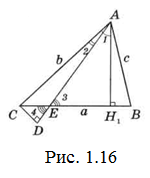
Доведення. Нехай в ∆АВС b>с і АЕ – даний відрізок (рис. 1.16).

Доведемо, що АЕ<b. Проведемо висоту АН₁. ˂l+C=90° (з ∆АН₁С). Тоді ˂2+C<90° і ˂3<90°, оскільки ˂3=˂2+C (зовнішній для ∆АСЕ). Значить, і вертикальний з ним ˂4<90°. Отже, висота в ∆АСЕ потрапить на продовження АЕ. У прямокутному ∆ACD AC>AD (гіпотенуза більше катета) і тим більше АС>АЕ, тобто АЕ< b, що і потрібно було довести.

Задача 23. Доведіть, що відрізок, розміщений між двома сторонами трикутника, менший найбільшої із сторін трикутника.

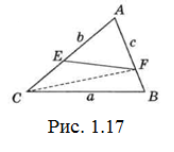
Доведення. Нехай сторона а найбільша, a EF – цей відрізок (рис. 1.17).

Проведемо CF. Тоді для ∆AFC EF<AF або EF<CF (у залежності від того, який з відрізків AF або CF більший).

Нехай AF більший і EF<AF. Але AF<AB=c і с<а (за умовою). Значить, EF<a. Нехай CF більший відрізок. Тоді EF<CF. Але для ∆АВС CF<a (оскільки а> b – найбільша сторона). І тим більше EF<a. Ми показали, що у будь-якому випадку EF<a. Що й потрібно було довести.

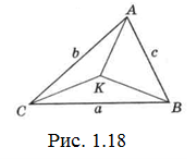
Задача 24. Доведіть, що для довільної точки К усередині трикутника ABC справедливо наступна нерівність: p<KA<KB<KC<2p (Рис. 1.18).

Доведення.

Ліва частина нерівності майже очевидна: КВ+КС>а; КС+КА>b і КА+КВ>с. Додавши ліві і праві частини і розділивши на 2, отримаємо потрібне. Помітимо також, що ліва частина нерівності виконується і для будь-якої точки К в площині ∆АВС (не обов’язково усередині).

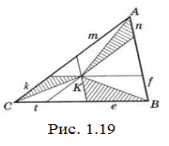
Для доведення правої частини нерівності проведемо через точку К прямі паралельно сторонам ∆АВС. Сторони отриманого паралелограма позначимо m і n, e і f, k і t (рис. 1.19).

Запишемо нерівність трикутника для трьох заштрихованих трикутників: КА<m+n; KB<e+f; KC<k+t. Додавши ліві і праві частини, отримаємо: KA+KB+KC<m+n+e+f+k+t. Оскільки сума m+n+e+f+k+t складає лише частину периметра ∆АВС, то КА+КВ+КС<2р.

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

 

1. Вишенський В.А., Ядренко М.Й. Вибрані задачі з алгебри й геометрії // К.: Вища школа, 1978, 72 с.
2. Коксетер Г.С., Грейтцер С.Л. Новые встречи с геометрией //М.: Наука, 1978, 224 с.
3. Прасков В.В. Задачи по планиметрии. Ч. 1 //М.: Наука, 1991, 320 с.
4. Прасков В.В. Задачи по планиметрии. Ч. 2 // М.: Наука, 1991, 240 с.
5. Федак І.В. Розв'язування рівнянь. Доведення нерівностей: Посібник для підготовки до математичних олімпіад у 9-10 класах //Тернопіль, 1997, 64 с.
6. Федак І.В. Довжини, кути, площі, цікаві лінії і точки // Тернопіль, 1998, 50 с.
7. Филипповский Г. Школьная геометрия в миниатюрах // Киев, “Грот”, 2002, 239с.
8. Яремчук М.Л., Попруженко М.Г. Збірник геометричних задач. Планіметрія //К., Радянська школа, 1996.