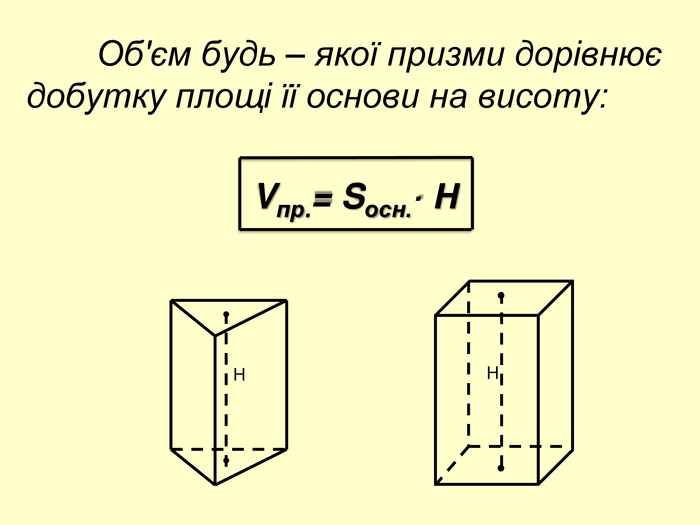
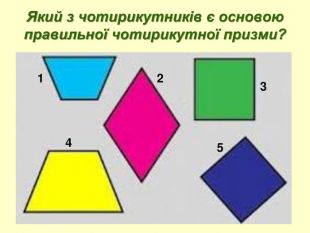
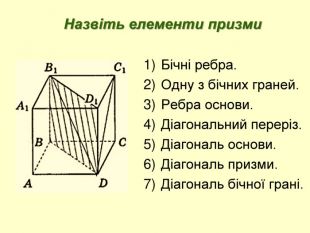
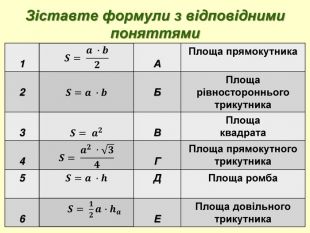
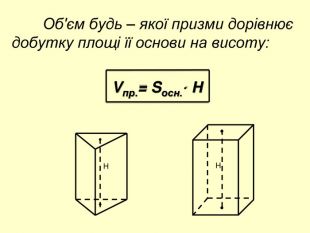
Додаток до уроку з геометрії для 11 класу з теми "Об'єм призми"
Про матеріал
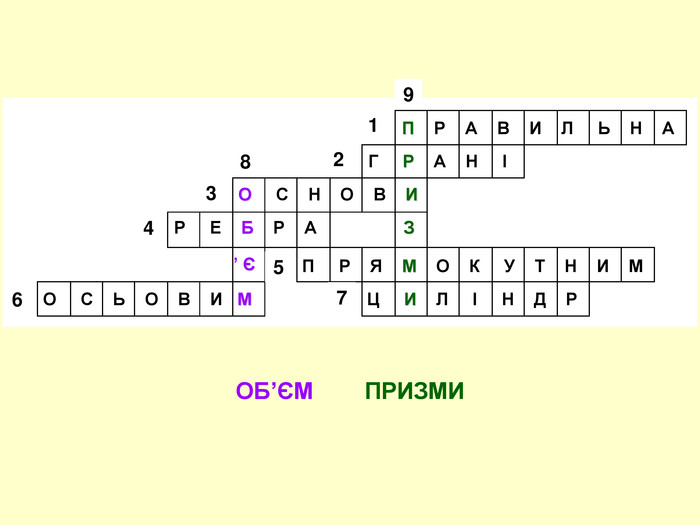
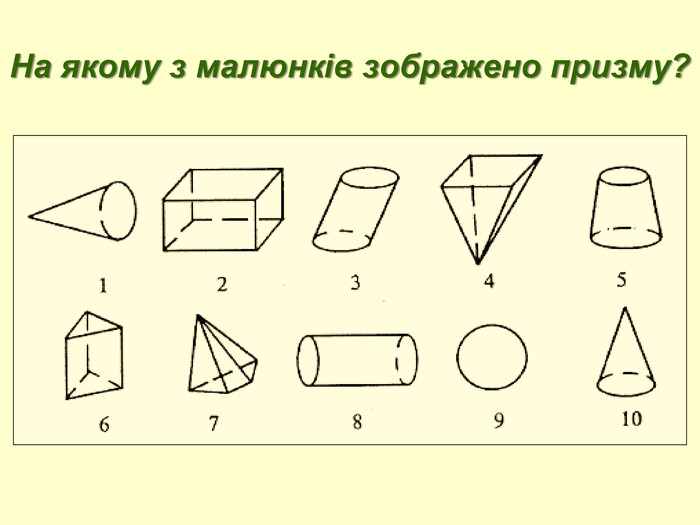
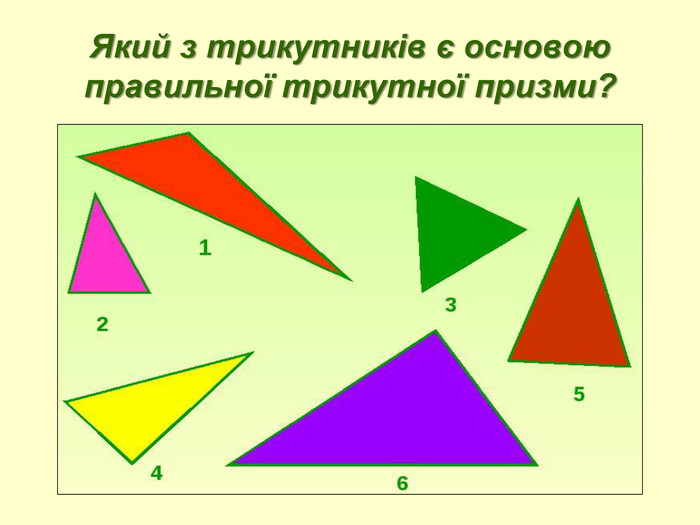
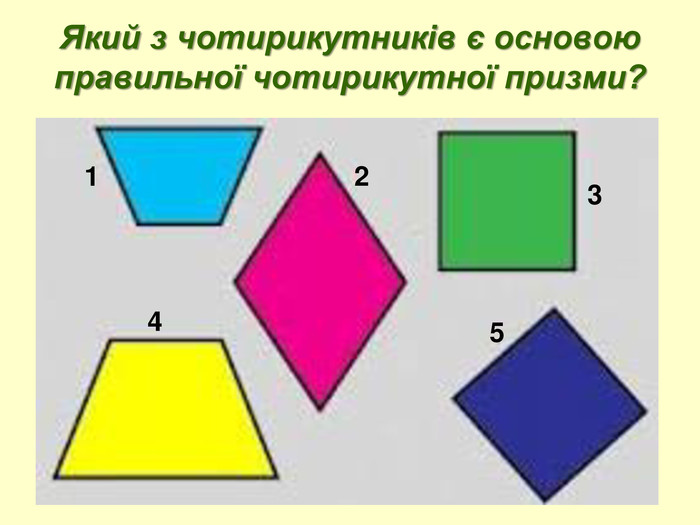
Матеріал містить презентацію з теми "Об'єм призми" і є додатком до уроку для учнів 11 класу. Презентація включає завдання з геометрії з професійним спрямуванням для професії "Кухар; кондитер" та технологію критичного мислення.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку