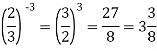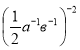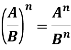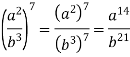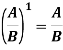Посібник для уроків алгебри І семестр 8 класу
Любі учні!
 Ти продовжуєш вивчати одну з найважливіших математичних дисциплін – алгебру. В оволодінні навчальним матеріалом курсу тобі допоможе цей посібник. Він складається з трьох блоків, кожен з яких містить уроки розбору матеріалу блоку, уроки фронтального опрацювання матеріалу, уроки внутрішньопредметного узагальнення. Також посібник містить завдання по підготовці до індивідуального опрацювання матеріалу, які позначені значком .
Ти продовжуєш вивчати одну з найважливіших математичних дисциплін – алгебру. В оволодінні навчальним матеріалом курсу тобі допоможе цей посібник. Він складається з трьох блоків, кожен з яких містить уроки розбору матеріалу блоку, уроки фронтального опрацювання матеріалу, уроки внутрішньопредметного узагальнення. Також посібник містить завдання по підготовці до індивідуального опрацювання матеріалу, які позначені значком .
Будь уважний, активний і наполегливий, не лінуйся і таким чином принесеш радість собі, своїм батькам і Творцю.
Нехай Бог посилає мудрості у вивченні алгебри!!!
Тема №1. Степінь з цілим показником
Урок №1

Степінь з цілим показником
«Вчора - вже пройшло, завтра – ще не
настало, щоб любити у мене є тільки СЬОГОДНІ»
Мати Тереза
Питання
- Степінь з цілим показником.
- Стандартний вигляд числа.
-
Функція
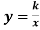 , її графік та властивості.
, її графік та властивості.
Література
Істер О.С. Алгебра: підручник для 8-го класу загальноосвітніх навчальних закладів, К.: Ґенеза, 2016 рік, § 9 – 12, стор. 69 – 111.
|
1. Степінь з цілим показником |
||
|
1.1 |
Степенем з цілим від’ємним показником називається дріб, чисельник якого дорівнює 1, а знаменник – є степеню з тією ж основою і додатним показником, тобто |
|
|
1.2 |
Властивості степеня з цілим показником
|
|
|
2. Стандартний вигляд числа |
||
|
2.3 |
Стандартним виглядом числа b називають його запис у вигляді добутку
|
2000000 =
0, 00004 = 4 |
|
3. Функція |
||
|
3.4 |
Оберненою пропорційністю називається функція, яку можна задати формулою виду |
|
|
3.5 |
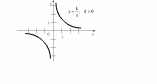
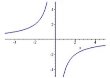
Криву, яка є графіком оберненої пропорційності, називають гіперболою. |
k > 0
k < 0
|
|
3.6 |
Властивості оберненої пропорційності 1. Область визначення функції – всі дійсні числа,
крім 0 (
2. Область значень – всі дійсні числа, крім 0 ( 3. Графік – гіпербола. 4. Якщо k > 0, то графік лежить у І і ІІІ координатних чвертях, якщо k < 0 – у ІІ і ІV. 5. Гілки гіперболи необмежено наближаються до осей координат. |
|
Уроки №2 – 4
«Одного разу ви зрозумієте, що ваша
велич починається там, де закінчується гординя»
Збірка «Хліб наш насущний»
Фронтальне опрацювання матеріалу
Означення та властивості степеня з цілим показником
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 1.2 блоку № 1.
- Усно дай відповідь на питання:
- Що називається степенем з цілим від’ємним показником?
- Сформулювати властивості степеня з цілим показником.
Завдання 2.
Розв’язати математичне кодування. В ньому схований рік народження французького лікаря та математика 15 століття.
![]()
![]()
![]()
![]()
1 4 4 5
У 1445 році народився великий математик Ніколя Шюке, який вперше ввів від’ємні та нульові степені. А пізніше Ісаак Ньютон став застосовувати їх систематично.
ІІ. Відпрацювання практичних умінь та навичок
Розв’яжи письмово вправи з підручника, стор. 72 – 79:
Завдання 3.
268 (1, 3, 5, 7, 9, 11, 13, 15); 272; 276 (2, 4, 6, 8, 10, 12); 278; 281.
Завдання 4.
Виконати завдання математичного лото, запропонованого вчителем.
Завдання 5.
- 304 (1, 3, 5, 7, 10, 12); 306; 308.
-
Спростіть вираз і дізнайтесь, які вітаміни найбільш потрібні для щоденного раціону людини.
-
|
|
|
|
|
|
|
А |
D |
B6 |
E |
С |
- Подай вирази у вигляді степеня і з’ясуй, в яких продуктах міститься найбільша кількість вітамінів.
|
|
|
|
|
|
|
|
|
|
|
|
молоко, кефір |
сир |
шоколад |
зелений перець |
кава |
печінка |
чіпси |
м’ясо |
кока-кола |
хліб |
- Знайшовши правильні відповіді, дізнаєтесь, які мінеральні речовини та мікроелементи необхідні нашому організму для повноцінного розвитку.
|
|
|
|
|
|
|
|
|
калій |
ртуть |
кальцій |
залізо |
сірка |
фтор |
натрій |
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач
Завдання 6.
-
Обчисли:
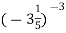 .
.
-
Спрости вираз: a)
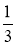 p-2q -5 ∙
p-2q -5 ∙ 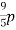 6q3; б)
6q3; б) 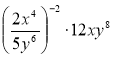 .
.
-
Спрости вираз:
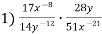 ; 2)
; 2) 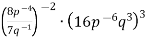
-
Обчисли:
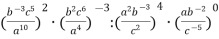

Готуємось до індивідуального опрацювання
-
Обчисли:
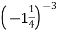 .
.
-
Спрости вираз: 1)
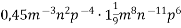 ; 2)
; 2) 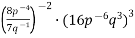 .
.
-
Спрости вираз:
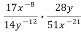 .
.
Уроки №6, 7
«Що умієте — не забувайте,
Що не вмієте — того учіться»
Володимир Мономах
Фронтальне опрацювання матеріалу
Стандартний вигляд числа
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 2.3 блоку № 1.
- Усно дай відповідь на питання:
- Що називається степенем з цілим від’ємним показником?
- Сформулювати властивості степеня з цілим показником.
- Що називають стандартним виглядом числа?
Завдання 2.
Розгляньте приклад розв’язування задачі

ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
- Запишіть у стандартному вигляді:
- число 38 000;
-
 число 190 000;
число 190 000;
-
число, що дорівнює масі Венері
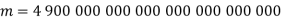 кг;
кг;
- число, що дорівнює масі атома Купруму
![]() кг.
кг.
- Розв’яжіть задачі і запишіть відповідь у стандартному вигляді:
- Одна пляшка лимонаду містить 78 000 калорій. Скільки кілокалорій отримує щодня Оксана з цього напою, якщо до її щоденного раціону сходить дві такі пляшки?
- Одна банка яблучного соку містить 46 000 калорій. Скільки кілокалорій отримує щодня Олег із цього напою, якщо до його щоденного раціону входить дві такі банки?
-
Маса Юпітера становить
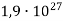 кг, а маса Марса –
кг, а маса Марса – 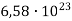 кг. Визначте у скільки разів маса Юпітера більша за масу Марса.
кг. Визначте у скільки разів маса Юпітера більша за масу Марса.
-
Маса Сатурна становить
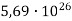 кг, а маса Землі –
кг, а маса Землі – 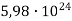 кг. Визначте у скільки разів маса Сатурна більша за масу Землі.
кг. Визначте у скільки разів маса Сатурна більша за масу Землі.
Завдання 4.
4.1. Подайте у вигляді степеня числа 10 вираз:
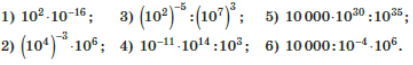
4.2. Визначте порядок числа:
![]()
4.3. Для того щоб зібрати 1 кг меду, бджола повинна облетіти 8 500 000 квітів білої акації та 4 000 000 квітів еспарцету. Визначте у скільки разів кількість квітів білої акації більша за кількість квітів еспарцету.
4.4. У таблиці наведена кількість запасів прісної води на Землі.

- Запишіть подані значення у стандартному вигляді.
- Визначте й запишіть:
А) у скільки разів кількість прісної води у льодовиках перевищує її кількість у річках та озерах;
Б) у скільки разів кількість прісної води у підземних джерелах менша від її кількості у льодовиках.
4.5. Спростіть вираз
![]()
та знайдіть його значення при ![]() .
.
Завдання 5.
5.1. Виконайте вправи 344, 350 ст. 84, 85 підручника.
5.2. Виконайте самостійно практичну роботу.
 Практична робота
Практична робота
 Тема. Стандартний вигляд числа.
Тема. Стандартний вигляд числа.
Мета: дати уявлення про стандартний вигляд числа.
Завдання. Подати у стандартному вигляді число 1) а = 4 350 000. 2) а = 0,000508
Хід роботи
1)
- У даному числі постав кому так, щоб у цілій частині залишилася одна цифра, відмінна від нуля.
- Запиши отримане число.
- Порахуй скільки цифр відокремили комою справа, помнож записане число на 10 в цьому степені.
- Запиши відповідь.
2)
- Перенеси кому вправо так, щоб у цілій частині залишилася одна цифра, відмінна від нуля.
- Запиши отримане число.
- Порахуй скільки цифр відокремили комою зліва.
- Зроби це число від’ємним – це показник степеня.
- Помнож число з п.2 на 10 зі знайденим показником.
- Запиши відповідь.

Очікуваний результат
- Отже, 4 350 000 = 4,35·106
Відповідь: 4,35·106 .
-
 Отже, 0,000508 = 5,08·10-4
Отже, 0,000508 = 5,08·10-4
Відповідь: 5,08·10-4.
Уроки №8, 9
«Алгебра – щедра, вона
часто дає більше, ніж в неї просять»
О. Суворов
Фронтальне опрацювання матеріалу
Функція ![]() , її графік і властивості
, її графік і властивості
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 3.4 – 3.6 блоку № 1.
- Усно дай відповідь на питання:
- Яка функція називається оберненою пропорційністю?
- Що є графіком оберненої пропорційності?
-
Перерахувати властивості оберненої пропорційності.
- Усно виконати вправи, запропоновані вчителем у презентації.
Завдання 2.
Усно розв’яжи вправи:
-
В яких координатних чвертях розміщений графік функції
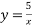 ?
?
|
А |
Б |
В |
Г |
|
І, ІV |
І, ІІ |
ІІ, ІV |
І, ІІІ |
-
Знайди значення функції
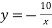 , якщо
, якщо  .
.
|
А |
Б |
В |
Г |
|
|
0,4 |
|
4 |
- Яка з наведених функцій є оберненою пропорційністю?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайди значення аргументу при якому значення функції
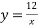 дорівнює 3:
дорівнює 3:
|
А |
Б |
В |
Г |
|
|
4 |
2 |
|
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Письмово розв’яжи вправи з підручника, стор. 92 – 94: 371; 373; 379; 384 (1, 2).
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач
Завдання 4.
Письмово розв’яжи вправи з підручника, стор. 93 – 94: 375; 374; 380.

Готуємось до індивідуального опрацювання
-
Виконай дії: 1)
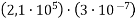 ; 2)
; 2) 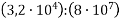 .
.
-
Запиши число у стандартному вигляді: 1)
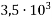 ; 2)
; 2) 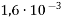 ; 3)
; 3) 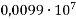 .
.
-
Задай формулою обернену пропорційність, якщо відомо, що її графік проходить через точку
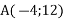 .
.
-
Знайди масу газу об’ємом V з густиною
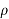 , якщо
, якщо 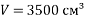 ;
; 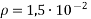 г/см³.
г/см³.
-
Знайди значення k, при якому графік функції
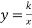 проходить через точку А (– 3; 4). Побудуй графік цієї функції.
проходить через точку А (– 3; 4). Побудуй графік цієї функції.
Урок №11
«Не будь переможений
злом, але перемагай зло добром»
Послання ап. Павла до колосян 12:21
Внутрішньопредметне узагальнення матеріалу
Степінь з цілим показником
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори блок № 1.
- Дай письмово відповідь на питання, запропоновані вчителем.
Завдання 2.
Усно виконай вправи:
-
Обчисли
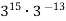 .
.
|
А |
Б |
В |
Г |
|
9 |
|
6 |
|
- Запиши у стандартному вигляді число 0,00213.
|
А |
Б |
В |
Г |
|
21,3 |
|
|
|
-
Спрости вираз
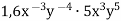 .
.
|
А |
Б |
В |
Г |
|
|
|
8у |
|
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 3.
Письмово виконай вправи:
-
Обчисли значення виразу:
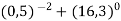 .
.
-
Виконай дії: 1)
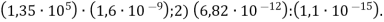 Результат запиши у стандартному вигляді.
Результат запиши у стандартному вигляді.
-
Обчисли:
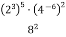 .
.
-
Спрости вираз:
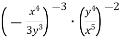 .
.
-
Розв’яжи графічно рівняння
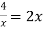 .
.
Тема №2. Раціональні вирази, додавання і віднімання раціональних виразів
Урок №1

Раціональні вирази, додавання та віднімання раціональних виразів
«І все, що тільки робите, словом
чи ділом, – усе робіть у Ім’я Господа Ісуса»
Послання ап. Павла до Колосян 3:17
Питання
- Раціональні вирази. Раціональні дроби.
- Основна властивість раціонального дробу.
- Додавання та віднімання раціональних дробів.
Література
Істер О.С. Алгебра: підручник для 8-го класу загальноосвітніх навчальних закладів, К.: Ґенеза, 2016 рік, § 1– 4 , стор. 5 – 38
|
||
|
1.1 |
Раціональні вирази – це математичні вирази, які містять дії додавання, віднімання, множення, ділення та піднесення до степеня з цілими показником. |
|
|
1.2 |
Якщо чисельник і знаменник дробу – многочлени, то дріб називають раціональним дробом. |
|
|
1.3 |
Значення змінних, при яких вираз має зміст, називають допустимими значеннями змінних у виразі. |
Допустимі значення змінної – всі числа, крім – 2. |
|
1.4 |
Всі допустимі значення змінних називають областю допустимих значень (ОДЗ) цього виразу. |
|
|
1.5 |
Щоб знайти допустимі значення змінних раціонального дробу, потрібно:
|
ОДЗ: |
|
1.6. |
Дріб дорівнює нулю, якщо чисельник цього дробу дорівнює нулю, а знаменник – не дорівнює нулю. |
|
|
||
|
2.7 |
Основна властивість дробу Якщо чисельник і знаменник дробу помножити або поділити на один і той самий вираз (що не дорівнює нулю), то одержимо дріб, що дорівнює даному. |
|
|
2.8 |
Скоротити дріб означає поділити чисельник і знаменник дробу на спільний дільник. |
|
|
2.9 |
Для того, щоб скоротити дріб, треба:
|
|
|
2.10 |
Якщо змінити знак у чисельнику (або знаменнику) дробу одночасно із знаком перед дробом, то одержимо дріб, тотожно рівний даному. |
|
|
||
|
3.11 |
Щоб додати (відняти) раціональні дроби з однаковими знаменниками, потрібно додати (відняти) їх чисельники, а знаменник залишити той самий. |
|
|
3.12 |
Щоб додати (відняти) раціональні дроби з різними знаменниками, потрібно:
|
|
Уроки №2, 3
«Для всього свій час, і година своя кожній
справі під небом: час мовчати і час говорити»
Книга Еклезіаста 3: 1, 7
Фронтальне опрацювання матеріалу
Раціональні вирази. Раціональні дроби
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 1.6 блоку № 2.
- Усно дати відповіді на питання:
- Який вираз називається раціональним?
- Які дроби називають раціональними?
- Що називають допустимими значеннями змінної ?
- Як знайти допустимі значення раціонального дробу?
-
Коли дріб дорівнює нулю?
- Переглянь скрайб-презентацію, запропоновану вчителем.
Завдання 2.
- Запам’ятай!

- Усно розв’яжи вправу 1, стор. 8 підручника.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
- Розглянь приклад:

- Користуючись розглянутим прикладом, письмово виконай вправи 4 (1), 6 стор. 8 підручника.
Завдання 4.
- Розглянь приклади:



- Користуючись розглянутими прикладами, письмово виконай вправи, стор. 9, 10 підручника: 7 (2, 4, 6, 8); 9; 11 (1, 3); 15 (1, 3); 13 (2, 4); 23.
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач
Завдання 5.
Виконай письмово вправу, запам’ятай інформацію і використовуй у житті.
|
|
ІМТ в межах 18,5-24,99 кг/м² – показник нормальної ваги.
При цьому об’єм талії у жінок не повинен перевищувати 80 см, а у чоловіків – 94 см |
Уроки №4 – 6
«...помилки друзів ми повинні уміти
виправляти або зносити, якщо вони не серйозні»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Основна властивість дробу. Скорочення дробів
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 2.9 блоку № 2.
- Усно відповісти на питання:
- Які дроби називаються раціональними?
- Що називають областю допустимих значень виразу?
- Як знайти ОДЗ раціонального дробу?
- Як читається основна властивість дробу?
- Що означає скоротити дріб?
- Як скоротити дріб?
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
Розглянь приклад.
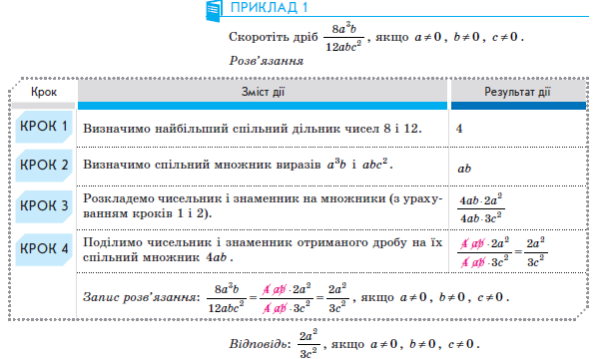
Завдання 3.
Користуючись розглянутим прикладом, письмово виконай вправи, стор. 15 – 16 підручника: 32 (1, 3, 5, 7); 37 (2, 4).
Завдання 4.
Розглянь приклад.

Завдання 5.
Користуючись розглянутим прикладом, письмово виконай вправу 39 (2, 4, 6, 8) стор. 16 підручника.
Завдання 6.
Розглянь приклад.

Завдання 7.
Користуючись розглянутим прикладом, письмово виконай вправи 43 (1, 3, 5), 44 стор. 17 підручника.
Завдання 8.
Виконай самостійно практичну роботу.
Практична робота №
 Тема. Основна властивість дробу. Скорочення дробу.
Тема. Основна властивість дробу. Скорочення дробу.
Мета: навчитись знаходити область визначення і будувати графік функції.
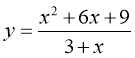 Завдання. Знайти область визначення і побудувати графік функції
Завдання. Знайти область визначення і побудувати графік функції
Хід роботи.
- Згадай, що знаменник нулю не дорівнює. Знайди область визначення функції.
- Виділи повний квадрат в чисельнику.
- Скороти дріб на спільний множник чисельника і знаменника.
- Встанови вид функції та її графік.
- Щоб побудувати графік потрібно скласти таблицю та врахувати область визначення.
- Точку, яка не входить в область визначення на графіку «виколюють».
- Зроби висновок.

Очікуваний результат.
|
х |
0 |
-3 |
|
у |
3 |
0 |
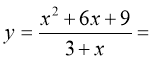
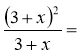
![]() ,
, ![]()


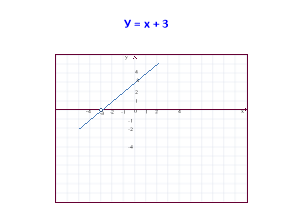
Завдання 9.
Розглянь приклад.

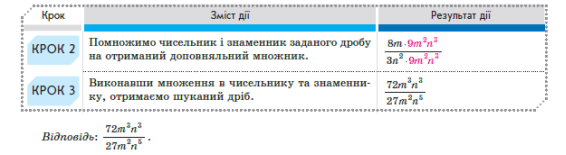
Завдання 10.
Користуючись розглянутим прикладом, письмово виконай вправу 35 стор. 16 підручника.
Завдання 11.
Розглянь приклад.
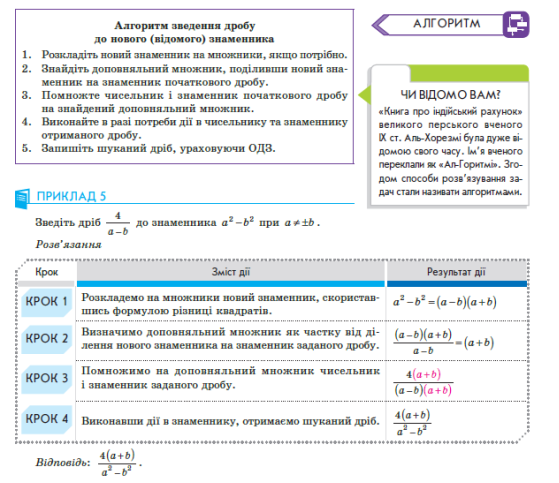
Завдання 11.
Користуючись розглянутим прикладом, письмово виконай вправу 45 (2, 4, 6) стор. 17 підручника.
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач
Завдання 12.
Письмово виконай вправи, стор. 18 підручника: 53; 49 (2, 4); 48.
Завдання 13.
Виконай самостійно вправу «Вірю – не вірю», запропоновану вчителем.

Готуємось до індивідуального опрацювання
-
Скоротіть дріб:
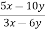 .
.
-
Зведіть дріб
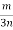 до знаменника
до знаменника 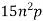 .
.
-
Знайдіть значення виразу
 , якщо c = 5.
, якщо c = 5.
-
Назвіть допустимі значення змінної у виразі
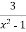 .
.
-
Скоротіть дріб
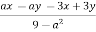 .
.
-
Знайдіть значення виразу
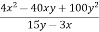 , якщо
, якщо 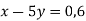 .
.
Уроки №8, 9
«У Господньому страхові сильна
надія, і Він пристановище дітям Своїм»
Книга приповістей Соломонових 14:26
Фронтальне опрацювання матеріалу
Додавання і віднімання дробів з однаковими знаменниками
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 3.10 блоку № 2.
- Усно дати відповіді на питання:
- Який вираз називається раціональним?
- Які дроби називають раціональними?
- Що називають допустимими значеннями змінної у виразі?
- Як знайти допустимі значення раціонального дробу?
- Як читається основна властивість дробу?
- Що означає скоротити дріб?
- Як скоротити дріб?
- Як додати (відняти) дроби з однаковими знаменниками?
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
- Запам’ятай алгоритм додавання (віднімання) дробів з однаковими знаменниками:

- Розглянь приклади 1 – 3, стор. 20 – 21 підручника .
Завдання 3.
Користуючись розглянутими прикладами, виконай письмово вправи, стор. 22 – 23 підручника: 63 (1, 3, 5); 65 (2, 4); 67, 70; 71 (1, 3).
Завдання 4.
Розглянь приклад, який допоможе подавати дріб у вигляді суми або різниці дробів чи у вигляді суми або різниці цілого виразу і дробу:

Завдання 5.
Користуючись розглянутим прикладом, виконай письмово вправи 73; 75; 76; 78 (2, 4), стор. 24 підручника.
Завдання 6.
Виконай письмово вправу, стор. 25 підручника: 80 (1, 3).
Уроки №10 – 12
«Бо Господь дає мудрість, з Його уст – знання й розум!»
Книга приповістей Соломонових 2:6
Фронтальне опрацювання матеріалу
Додавання і віднімання дробів з різними знаменниками
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити блок № 2.
- Усно дати відповіді на питання:
- Який вираз називається раціональним?
- Які дроби називають раціональними?
- Що називають допустимими значеннями змінної ?
- Як знайти допустимі значення раціонального дробу?
- Як читається основна властивість дробу?
- Що означає скоротити дріб?
- Як скоротити дріб?
- Як додати (відняти) дроби з однаковими знаменниками?
- Як додати (відняти) дроби з різними знаменниками?
Завдання 2.
- Запам’ятай алгоритм знаходження спільного знаменника дробів:
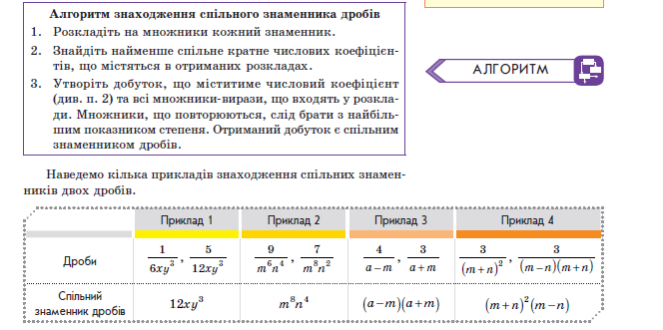
- Усно виконай вправи:

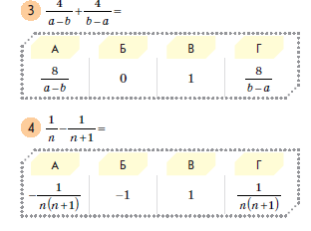
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Розглянь приклади 1, 2 на стор. 27 підручника.
Користуючись розглянутими прикладами, письмово розв’яжи вправи, стор. 29 – 30 підручника: 88; 90 (1, 3); 93 (2, 4).
Завдання 4
Розглянь приклади 3, 4 на стор. 28 – 29 підручника.
Користуючись розглянутими прикладами, письмово розв’яжи вправи, стор. 30 – 32 підручника:
95 (2, 4); 101; 115 (1, 3); 112 (2, 4).
ІІІ. Відпрацювання навичок розв’язування нестандартних задач
Завдання 5.
- Виконай самостійно вправу «Вірю – не вірю», запропоновану вчителем.

Готуємось до індивідуального опрацювання
-
Виконайте віднімання дробів:
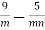 .
.
-
Виконайте додавання дробів:
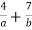 .
.
-
Перетворіть у дріб вираз:
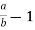 .
.
-
Виконайте дії:
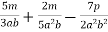 .
.
-
Подайте у вигляді дробу:
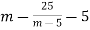 .
.
-
Спростіть вираз:
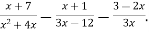
Урок №14
«Життя стане простішим, якщо прочитати
 до нього інструкцію»
до нього інструкцію»
Автор невідомий
Внутрішньопредметне узагальнення матеріалу
Додавання та віднімання дробів
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори блок № 2.
- Дай письмово відповідь на питання, запропоновані вчителем.
Завдання 2.
Усно виконай вправи:
-
Знайдіть значення виразу:
 , якщо
, якщо 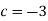
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Скоротіть дріб:

|
А |
Б |
В |
Г |
|
|
|
|
|
-
Вкажіть допустимі значення змінної у виразі:
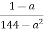 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 3.
Письмово виконай вправи:
-
Виконайте дії:
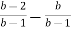
-
Перетворіть у дріб вираз:
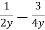 .
.
-
Скоротіть дріб:
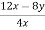 .
.
Завдання 4.
-
Спростіть вираз:
 .
.
-
Скоротіть дріб:
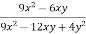 .
.
-
Доведіть тотожність:
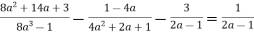
Тема №3. Множення та ділення раціональних виразів. Раціональні рівняння
Урок №1

«Не той дурний, хто не
знає... але той, хто знати не хоче»
Григорій Сковорода
Множення та ділення раціональних дробів. Раціональні рівняння
Питання
- Множення та ділення раціональних дробів.
- Тотожні перетворення раціональних виразів.
- Раціональні рівняння.
Література
Істер О.С. Алгебра: підручник для 8-го класу загальноосвітніх навчальних закладів, К.: Ґенеза, 2016 рік, § 5 – 8, стор. 38 – 69.
|
1. Множення та ділення раціональних дробів |
||||
|
1.1. |
Щоб помножити два раціональні дроби, слід перемножити окремо їх чисельники та окремо знаменники і записати перший добуток у чисельник, а другий – у знаменник нового дробу:
|
|
||
|
1.2. |
При множенні раціонального дробу на цілий вираз у чисельнику записують добуток чисельника на цей вираз, а знаменник зберігається:
|
|
||
|
1.3. |
Щоб піднести дріб до степеня, слід піднести до цього степеня окремо чисельник та окремо знаменник і записати перший результат у чисельник, а другий – у знаменник нового дробу:
|
|
||
|
Запам’ятай!
|
||||
|
1.4. |
Щоб поділити один раціональний дріб на другий, слід перший дріб помножити на дріб, обернений до другого дробу:
|
|
||
|
2. Тотожні перетворення раціональних виразів |
||||
|
2.5. |
Будь-який раціональний вираз можна подати у вигляді раціонального дробу, виконуючи його тотожне перетворення, тобто виконуючи всі дії, які містить цей вираз (додавання, віднімання, множення, ділення, піднесення до степеня) за правилами виконання дій.
|
|||
|
3. Раціональні рівняння |
||||
|
3.6. |
Рівняння називаються раціональним, якщо його ліва і права частини є раціональними виразами. |
|||
|
3.7. |
Рівняння називають цілим (або цілим раціональним), якщо його ліва і права частини є цілими раціональними виразами. |
|
||
|
3.8. |
Рівняння називають дробовим (або дробово-раціональним), якщо хоча б одна з його частин є дробовим раціональним виразом. |
|
||
|
3.9. |
Два дробово-раціональних рівняння називаються рівносильними, всі розв’язки першого рівняння є розв’язками другого рівняння, і навпаки, усі розв’язки другого рівняння є розв’язками першого. Рівносильними вважають і ті рівняння, які не мають розв’язків. Запам’ятай!
|
|||
|
3.10 |
Значення змінної, при яких мають зміст вирази в обох частинах рівняння, називають областю допустимих значень (ОДЗ) рівняння. |
|||
|
3.11 |
Способи розв’язування дробово-раціональних рівнянь: |
|||
|
1.Зведення даного рівняння до виду |
2. Зведення даного рівняння до пропорції |
3. Множення обох частин рівняння на спільний знаменник
|
||
4) виключити з його коренів ті, які не належать ОДЗ. |
3) за властивістю пропорції записати дане рівняння у вигляді цілого 4) виключити з його коренів ті, які не належать ОДЗ. |
2) знайти спільний знаменник обох частин рівняння;
5) виключити з його коренів ті, які не належать ОДЗ. |
||
|
3.12 |
Під час розв’язування дробово-раціональних рівнянь отримані значення змінної можна перевірити одним з двох способів:
|
|||
Уроки №2, 3
«Любов нехай буде нелицемірна;
ненавидьте зло та туліться до доброго!»
Послання апостола Павла до римлян 12:9
Фронтальне опрацювання матеріалу
Множення дробів. Піднесення дробу до степеня
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 1.3 блоку № 3.
- Усно дай відповіді на питання:
- Сформулюй правило множення раціональних дробів.
- Як помножити раціональний дріб на цілий вираз?
- Як піднести до степеня раціональний дріб?
- Як піднести раціональний дріб до першого степеня?
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
- Розглянь приклад розв’язування вправи:
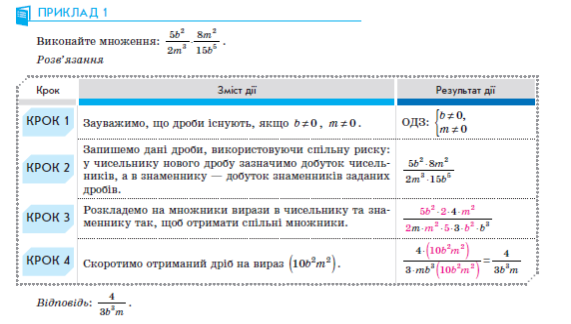
- Користуючись розглянутим прикладом, виконай письмово вправи, стор. 41 – 43 підручника: 141 (1, 3, 5); 143 (2, 4, 6); 151 (2); .
Завдання 3.
- Розглянь приклад розв’язування вправи.
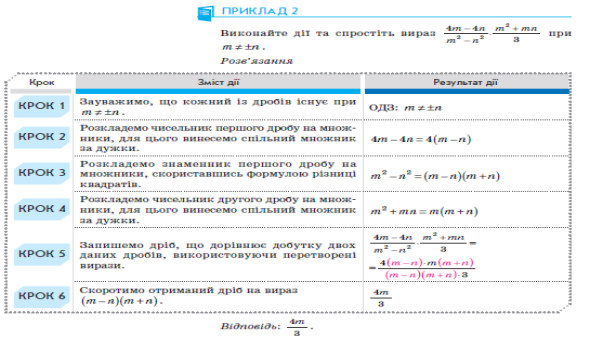
- Користуючись розглянутим прикладом, виконай письмово вправи, стор. 42 – 43 підручника: 147 (1, 3, 5); 153 (1); 155 (4).
- Завдання для роботи в групах
Письмово виконайте вправи:
|
Група № 1 |
Група № 2 |
Група № 3 |
Група № 4 |
Група № 5 |
|
153 (2); 155 (3) |
154 (1); 155 (2) |
154 (2); 155 (1) |
153 (2); 156 (1) |
154 (1); 156 (2) |
Завдання 4.
- Розглянь приклад розв’язування вправи.

- Користуючись розглянутим прикладом, виконай письмово вправи, стор. 42 – 43 підручника: 149 (6); 157 (2).
- Завдання для роботи в групах
Письмово виконайте вправи:
|
Група № 1 |
Група № 2 |
Група № 3 |
Група № 4 |
Група № 5 |
|
149 (1); 158 (2) |
149 (2); 158 (1) |
149 (3); 157 (1) |
149 (4); 158 (1) |
149 (5); 157 (1) |
ІІІ. Відпрацювання умінь та навичок розв’язування нестандартних задач
Завдання 5.
Виконай письмово вправи, стор. 44 підручника: 159 (1); 160 (2); 161.
Уроки №4, 5
«Хіба не любов усе єднає, будує,
творить, подібно до того, як ворожість руйнує»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Ділення раціональних дробів
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 1.4 блоку № 3.
- Усно дай відповіді на питання:
- Сформулюй правило множення раціональних дробів.
- Як піднести до степеня раціональний дріб?
- Як помножити раціональний дріб на цілий вираз?
- Сформулюй правило ділення раціональних дробів.
Завдання 2.
Виконай усно вправи.
-
Назви вираз, обернений до виразу: 1)
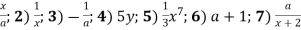 .
.
- Чи правильно замінено ділення множенням у виразах:
1) ![]() ; 3)
; 3) ![]()
2)![]() ; 4)
; 4)![]() ?
?
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
-


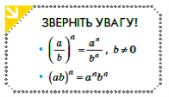 Пригадай та зверни увагу на окремі правила, які допоможуть виконувати дії з раціональними дробами:
Пригадай та зверни увагу на окремі правила, які допоможуть виконувати дії з раціональними дробами:
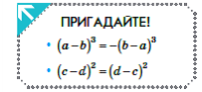
- Розглянь приклад 1, стор. 45 підручника.
- Користуючись розглянутим прикладом, виконай вправи, стор.46 – 47 підручника: 167 (1; 3); 169 (2; 4; 6; 8); 171 (1; 3).
Завдання 4.
- Розглянь приклад 2, стор. 46 підручника.
- Користуючись розглянутим прикладом, виконай вправи, стор.47 – 48 підручника: 173 (1; 3; 5); 175 (2; 4).
Завдання 5.
- Поділіться на групи, запропонованим учителем способом.
- Переглянь ще раз нагадування із завдання 3.1.
- Виконайте завдання, запропоноване вашій групі.
|
№ |
Зима |
Весна |
Літо |
Осінь |
|
1. |
Вправа 174 (1) |
Вправа 174 (2) |
Вправа 174 (3) |
Вправа 174 (4) |
|
2. |
Вправа 176 (4) |
Вправа 176 (3) |
Вправа 176 (2) |
Вправа 176 (1) |
|
3. |
Спростіть вираз
та обчисліть його значення, якщо |
Спростіть вираз
та обчисліть його значення, якщо |
Спростіть вираз
та обчисліть його значення, якщо |
Спростіть вираз
та обчисліть його значення, якщо |
|
4. |
Спростіть вираз
та обчисліть його значення, якщо |
Спростіть вираз
та обчисліть його значення, якщо |
Спростіть вираз
та обчисліть його значення, якщо |
Спростіть вираз
та обчисліть його значення, якщо |
|
5. |
Спростіть вираз
та обчисліть його значення, якщо число b становить 25 % числа a |
Спростіть вираз
та обчисліть його значення, якщо число y становить 20 % числа x |
Спростіть вираз
та обчисліть його значення, якщо число b становить 25 % числа a |
Спростіть вираз
та обчисліть його значення, якщо число y становить 20 % числа x |
|
|
Підказка
|
|||
Завдання 6.
Письмово виконайте вправу:



Готуємось до індивідуального опрацювання
-
Подайте у вигляді дробу:
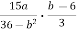
-
Спростіть вираз:
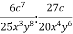
-
Подайте у вигляді дробу:
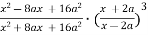
Уроки №7, 8
«Для всього свій час, і година
своя кожній справі під небом»
Книга Еклезіястова 3:1
Фронтальне опрацювання матеріалу
Тотожні перетворення раціональних виразів
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 2.5 блоку № 3.
- Усно дати відповідь на питання:
- Що є добутком раціональних дробів?
- Як раціональний дріб помножити на цілий вираз?
- Чому дорівнює степінь раціонального дробу?
- Як поділити два раціональні дроби?
- Що таке тотожне перетворення раціонального виразу?
Завдання 2.
Розглянути приклад розв’язування вправи.
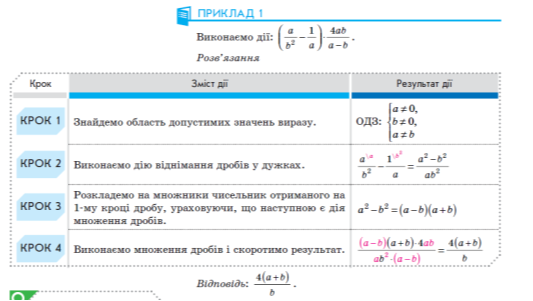

ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
- У завданнях 1 – 4 доведіть тотожність:
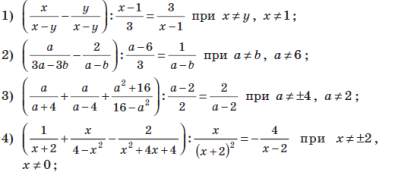
- Виконайте дії та спростіть вираз:
![]()
- Спростіть вираз:
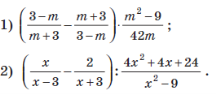
- Виконайте дії:

![]()
- Спростіть вираз та знайдіть його значення:
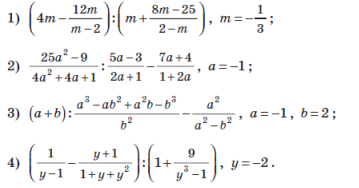
Завдання 4.
- Визначте чи є тотожно рівними вирази:
![]()
- Спростіть вираз:
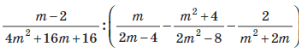
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач
Завдання 5.

Уроки №9 – 11
«Для всього свій час, і година своя кожній
справі під небом: час мовчати і час говорити»
Книга Еклезіаста 3: 1, 7
Фронтальне опрацювання матеріалу
Раціональні рівняння
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 3.6 – 3.11 блоку № 3.
- Усно дати відповіді на питання:
- Які рівняння називаються раціональними?
- Які рівняння називаються цілими раціональними рівняннями?
- Які рівняння називаються дробово-раціональними рівняннями?
- Які рівняння називаються рівносильними?
- Що таке область допустимих значень рівняння?
- Як читається умова рівності дробу нулю?
- Які є способи розв’язування дробово-раціональних рівнянь?
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
2.1. Виконати усно вправи, запропоновані вчителем у презентації.
2.2.Письмово розв’язати вправи з підручника, (стор. 76 – 28):
233; 235; 239; 245 (1); 249; 251 (1); 241, 243.
Завдання 3.
Розв’яжи рівняння:
3.1. ![]()
3.2. ![]()
3.3. ![]()
3.4. ![]()
-
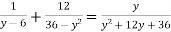 .
.
Завдання 4.
Виконати вправу «Вірю – не вірю», запропоновану вчителем.

Готуємось до індивідуального опрацювання
-
Розв’яжи рівняння:
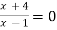 .
.
-
Подай вираз
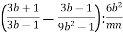 у вигляді дробу.
у вигляді дробу.
- Довести тотожність:
![]() .
.
- Чисельник дробу на 5 менший від знаменника. Якщо до чисельника додати 11, а від знаменника відняти 2, то одержимо дріб, обернений даному. Знайдіть початковий дріб.
Урок №13
«Не досить оволодіти премудрістю,
потрібно також вміти користуватися нею»
Народне прислів’я
Внутрішньопредметне узагальнення матеріалу
Множення та ділення раціональних дробів. Раціональні рівняння
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори блок № 3.
- Дай письмово відповідь на питання, запропоновані вчителем.
Завдання 2.
Усно виконати вправи:
- Вкажи дробове раціональне рівняння.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Піднеси до степеня дріб
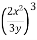 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Яке з чисел є коренем рівняння
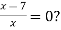
|
А |
Б |
В |
Г |
|
– 7 |
0 |
7 |
1 |
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 3.
Письмово виконай вправи:
-
Подайте у вигляді дробу:
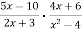 .
.
-
Спростіть вираз:
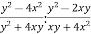 .
.
-
Розв’язати рівняння:
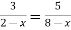 .
.
-
Виконати дії:
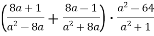 .
.
-
При якому значенні
 різниця дробів
різниця дробів 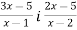 дорівнює 1?
дорівнює 1?
Тема №4. Повторення матеріалу, вивченого у І семестрі
Урок №1
«Золоті яблука на срібнім
тарелі – це слово, проказане часу свого»
Книга Приповістей Соломонових 25:11
Внутрішньопредметне узагальнення матеріалу
Узагальнення матеріалу, вивченого у І семестрі
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори блоки № 1 – 3.
- Усно дай відповідь на питання:
- Які дроби називаються раціональними?
- Що називають областю допустимих значень раціонального дробу?
- Як додати (відняти) дроби з різними показниками?
- Як помножити раціональні дроби?
- Як поділити раціональні дроби?
- Що називають степенем з від’ємним цілим показником?
- Сформулюй властивості степеня з цілим показником.
- Що називають стандартним виглядом числа?
- Що таке обернена пропорційність?
- Що є графіком оберненої пропорційності?
Завдання 2.
Усно розв’яжи вправи:
-
При яких значеннях змінної
 вираз
вираз 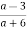 не має змісту?
не має змісту?
|
А |
Б |
В |
Г |
|
–3 |
3 |
6 |
–6 |
-
Обчисли:
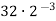 .
.
|
А |
Б |
В |
Г |
|
4 |
|
|
|
- Запиши у стандартному вигляді число 0,0000015.
|
А |
Б |
В |
Г |
|
|
|
|
|
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 3.
Письмово розв’яжи вправи:
-
Виконай додавання:
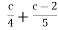 .
.
-
Знайди різницю:
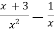 .
.
-
Розв’яжи рівняння:
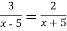 .
.
-
Виконати дії:
 ; 2
; 2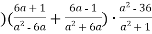
-
Розв’яжи графічно рівняння: :
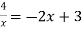 .
.
1


про публікацію авторської розробки
Додати розробку