Посібник для уроків геометрії І семестр 10 класу
Ківерцівська експериментальна школа
Навчальний посібник

І семестр


Шановний десятикласнику!
 Ти продовжуєш вивчати одну з найдавніших і найважливіших наук – математику. Курс математики 10 класу складається з двох частин – алгебри та геометрії. В оволодінні навчальним матеріалом геометрії тобі допоможе цей посібник. Він складається з двох блоків, кожен з яких містить уроки розбору матеріалу блоку, уроки фронтального опрацювання матеріалу, уроки внутрішньопредметного узагальнення. Також посібник містить завдання по підготовці до індивідуального опрацювання матеріалу, які позначені значком .
Ти продовжуєш вивчати одну з найдавніших і найважливіших наук – математику. Курс математики 10 класу складається з двох частин – алгебри та геометрії. В оволодінні навчальним матеріалом геометрії тобі допоможе цей посібник. Він складається з двох блоків, кожен з яких містить уроки розбору матеріалу блоку, уроки фронтального опрацювання матеріалу, уроки внутрішньопредметного узагальнення. Також посібник містить завдання по підготовці до індивідуального опрацювання матеріалу, які позначені значком .
Будь уважний, активний і наполегливий, не лінуйся і таким чином принесеш радість собі, своїм батькам і Творцю.
Нехай Бог посилає мудрості у вивченні алгебри!!!
Тема №1. Аксіоми стереометрії. Паралельність прямих у просторі. Паралельність прямої і площини
Урок №1

Аксіоми стереометрії. Паралельність прямих у просторі. Паралельність прямої і площини
Математик, подібно до художника чи поета, -
творець форм… Перше випробування – краса.
Г. Харді
Питання
- Основні поняття, аксіоми стереометрії
- Найпростіші наслідки з аксіом стереометрії
- Взаємне розміщення прямих у просторі
- Властивості і ознака паралельності прямих
- Розміщення прямої та площини у просторі
Література
Істер О.С. Математика: (алгебра і початки аналізу та геометрія, рівень стандарту): Підручник для 10 класу закладів загальної середньої освіти. Київ: Генеза, 2018 рік, розділ Геометрія, §§1 – 2, 4, стор. 224 – 248, 259 – 267.
|
1. Основні поняття, аксіоми стереометрії та найпростіші наслідки із них |
||||||
|
1.1 |
Стереометрія – це розділ геометрії, в якому вивчаються властивості фігур у просторі. |
|||||
|
1.2 |
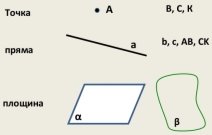
Основними фігурами стереометрії є точка, пряма і площина.
|
|
||||
|
1.3 |
|
|
||||
|
1.4 |
|
|
||||
|
1.5 |
|
|
||||
|
1.6 |
|
|
||||
|
2. Найпростіші наслідки з аксіом стереометрії |
||||||
|
2.7 |
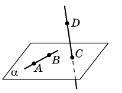
Наслідок 1. Через пряму і точку, що не лежить на ній, можна провести площину, і до того ж тільки одну. |
|
||||
|
2.8 |
Наслідок 2. Через дві прямі, що перетинаються можна провести площину і до того ж тільки одну.
|
|
||||
|
2.9 |
Площину можна задати:
|
|||||
|
3. Взаємне розміщення прямих у просторі |
||||||
|
3.10 |
Якщо дві прямі у просторі мають одну спільну точку, то кажуть, що вони перетинаються. |
A
b
|
||||
|
3.11 |
Прямі, які лежать в одній площині і не перетинаються, називаються паралельними. |
|
||||
|
3.12 |
Прямі, які не лежать в одній площині, називаються мимобіжними. |
|
||||
|
4. Властивості і ознака паралельності прямих |
||||||
|
Властивості паралельних прямих |
||||||
|
4.13 |
Теорема Основна властивість паралельних прямих у просторі Через точку простору, яка не лежить на даній прямій, можна провести пряму, паралельну даній, і тільки одну.
|
|
||||
|
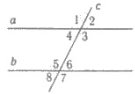
4.14 |
Якщо прямі паралельні, то: 1) внутрішні різносторонні кути, утворені цими прямими і січною, рівні; 2) сума внутрішніх односторонніх кутів дорівнює 180°; 3) відповідні кути рівні; і навпаки, якщо дві прямі перетнуто січною і: 1) внутрішні різносторонні кути, утворені при цьому, рівні, то ці прямі паралельні; 2) сума внутрішніх односторонніх кутів дорівнює 180°, то ці прямі паралельні; 3) відповідні кути рівні, то ці прямі паралельні. |
1)
2)
3)
|
||||
|
4.15 |
Теорема Якщо одна з двох паралельних прямих перетинає площину, то і друга пряма перетинає цю площину. |
|
||||
|
4.16 |
Теорема Ознака паралельності прямих Дві прямі, паралельні третій прямій, паралельні між собою. |
|
||||
|
4.17 |
Теорема Ознака мимобіжних прямих Якщо одна з двох прямих лежить у деякій площині, а друга пряма перетинає цю площину у точці, що не належить першій прямій, то ці прямі – мимобіжні. |
|
||||
|
5. Розміщення прямої і площини у просторі |
||||||
|
5.18 |
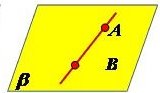
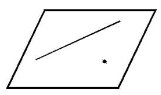
Якщо пряма має з площиною безліч спільних точок, то кажуть, що вона належить площині. |
|
||||
|
5.19 |
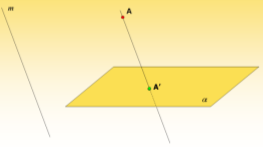
Якщо пряма має з площиною лише одну спільну точку, то кажуть, що вони перетинаються. |
|
||||
|
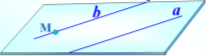
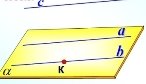
5.20 |
Якщо пряма і площина не мають спільних точок, то вони називаються паралельними. |
|
||||
|
5.21 |
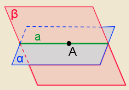
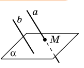
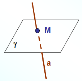
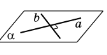
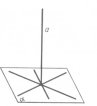
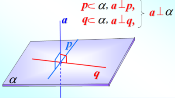
Теорема Ознака паралельності прямої і площини Якщо пряма, яка не належить площині, паралельна якій – небудь прямій в цій площині, то вона паралельна і самій площині. |
|
||||
|
5.22 |
Теорема Обернена до ознаки паралельності прямої і площини Якщо дана пряма паралельна площині, то в цій площині знайдеться пряма, паралельна даній прямій. |
|||||
|
5.23 |
Наслідок. Якщо пряма паралельна площині, то через будь-яку точку цієї площини можна провести пряму, паралельну даній, і до того ж тільки одну. |
|||||
Урок №2
І все, що тільки чините, робіть від душі,
немов Господеві, а не людям!
Послання до колосин 3:23
Фронтальне опрацювання матеріалу
Основні поняття стереометрії. Аксіоми стереометрії та наслідки з них
І. Робота над засвоєнням термінів, понять і правил
Завдання 1.
Повторіть тези 1.1. – 2.9 блоку №1 і дайте відповіді на запитання:
- Назвіть основні фігури стереометрії.
- Якщо дві різні площини мають спільну точку, то ________, що проходить через цю точку.
- Через пряму і точку, _________, можна провести площину, і до того ж тільки одну.
- Через три точки, які ________, можна провести площину, і до того ж тільки одну.
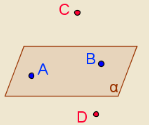
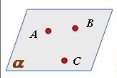
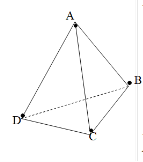
- Скільки площин можна провести через точки А, В, С? Відповідь обґрунтуйте.
- Дайте визначення стереометрії.
Завдання 2.
Усно дайте відповіді на питання:
-
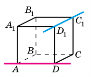
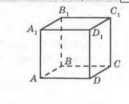
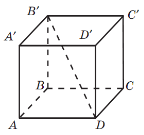
На рисунку зображено куб
 . Вкажіть точку, яка належить площині
. Вкажіть точку, яка належить площині 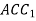 і точку, яка не належить площині
і точку, яка не належить площині 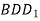 .
.
-
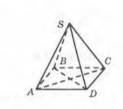
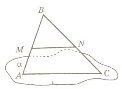
На рисунку зображено чотирикутну піраміду
 . Укажіть пряму, по якій перетинаються площини
. Укажіть пряму, по якій перетинаються площини  .
.
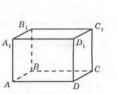
-
На рисунку зображено прямокутний паралелепіпед
 . Укажіть пряму, яка належить площині
. Укажіть пряму, яка належить площині 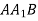 .
.
ІІ. Відпрацювання умінь і навичок розв’язування задач, застосування правил
Завдання 3.
Письмово розв’язати вправи:
-
Площини
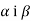 перетинаються по прямій
перетинаються по прямій 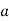 . У площині
. У площині 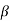 проведено пряму
проведено пряму 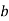 , яка перетинає площину
, яка перетинає площину  . Доведіть, що точка перетину прямої
. Доведіть, що точка перетину прямої 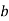 і площини
і площини  належить прямій
належить прямій 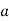 .
.
- Прямі АD і ВС не лежать в одній площині. Доведіть, що прямі АС і ВD не лежать в одній площині.
- Доведіть, що через дві довільні точки можна провести хоча б одну площину.
- Через три точки можна провести дві різні площини. Як розташовані ці точки?
-
Площини
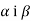 перетинаються по прямій
перетинаються по прямій 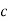 . Доведіть, що існує ще одна площина, відмінна від площин
. Доведіть, що існує ще одна площина, відмінна від площин 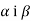 , яка містить пряму с.
, яка містить пряму с.
Урок №3
“Коли добре щось умієте – того
не забувайте, а чого не вмієте – того учітесь…”
Володимир Мономах
Фронтальне опрацювання матеріалу
Аксіоми стереометрії
І. Робота над засвоєнням термінів, понять і правил
Завдання 1.
- Повторіть тези 1.1 – 2.9 блоку № 1.
- Дайте відповіді на питання:
- Як можна задати площину?
- Яке мінімальне число точок визначає пряму в просторі?
- Чи можуть дві площини мати тільки одну спільну точку?
- Скільки площин можна провести через одну пряму?
- Скільки площин можна провести через пряму і точку?
- Як розміщені пряма а і точка А , якщо через них можна провести дві різних площини?
- П’ять точок не лежать в одній площині. Яке найбільше число цих точок може лежати на одній прямій?
ІІ. Відпрацювання умінь і навичок розв’язування вправ, застосування правил
Завдання 2.
Усно виконайте вправи:
- Скільки площин можна побудувати через виділені елементи?
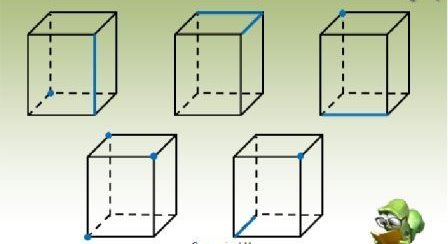
- Виконайте усно вправу 1.7 на ст. 232.
Завдання 3.
- Користуючись даним малюнком назвіть:
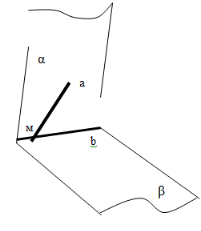
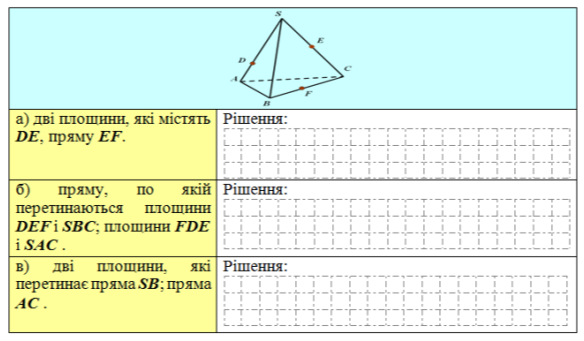
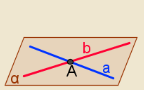
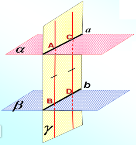
- Площини α та β перетинаються по прямій b. Пряма а лежить у площині α та перетинає площину β у точці М. Доведіть, що точка М лежить на прямій b.
Підказка до рішення задачі
Заповніть пропуски:
1) М ![]() α, М
α, М ![]() а, α ∩ β = b (за умовою)
а, α ∩ β = b (за умовою)
2) Тоді, М ![]() … (якій площині?).
… (якій площині?).
3) Отже, М – спільна точка … (яких площин?);
4) А значить, М ![]() b (чому ? за якою аксіомою?)
b (чому ? за якою аксіомою?)
- Виконати письмово вправи 1.25, 1.33, 1.51 ст. 233
 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
- Скільки різних площин можна провести через точки А, В і С, якщо вони не лежать на одній прямій?
-
Зобразіть куб
 . Вкажіть пряму, по якій перетинаються площини
. Вкажіть пряму, по якій перетинаються площини 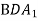 і
і 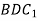 .
.
- Дано пряму а і точку А поза нею. Доведіть, що пряма с, яка проходить через точку А і перетинає пряму а, лежить із ними в одній площині.
- Прямі АD і ВС не лежать в одній площині. Доведіть, що прямі АС і ВD не лежать в одній площині.
Урок №5
«Геометрія — це інтуїція»
Г. Гельмгольц
Фронтальне опрацювання матеріалу
Розміщення двох прямих у просторі
І. Робота над засвоєнням термінів, понять і правил
Завдання 1.
- Повторіть тези 1.1 – 3.12 блоку №1.
- Дайте відповідь на питання:
- Назвіть основні поняття стереометрії.
- Стереометрія – це …
- Як зображають площину?
- Назвіть три способи задання площини.
- Як можуть бути розміщені прямі у просторі? Дайте визначення кожному розміщенню.
ІІ. Відпрацювання умінь і навичок, застосування правил
Завдання 2.
Користуючись рисунком, визначте взаємне розміщення прямих i заповнiть таблицю.
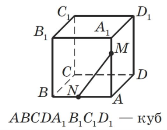
|
Прямі |
AB |
BB1 |
A1D1 |
|
MN |
|
|
|
|
C1A1 |
|
|
|
|
C1B1 |
|
|
|
Завдання 3.
Допишіть розв’язування задачі:
|
Дано чотири точки, що не лежать в одній площині. Скільки можна провести різних площин, які проходять через три з цих точок. Відповідь поясніть.
|
|
Нехай точки А, В, С, D не лежать … Ці точки і ніякі три з них … на одній прямій (чому?), тому кожна із чотирьох можливих трійок точок: А,В,С; …;…; …; визначають …. Ці чотири площини різні. Відповідь: _____________ |
Завдання 4.
- Точки А, В, С і D не лежать в одній площині. Доведіть, що прямі АВ і СD мимобіжні.
-
Прямі
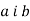 паралельні. Через точку М, що не належить цим прямим, проведено пряму, яка перетинає прямі
паралельні. Через точку М, що не належить цим прямим, проведено пряму, яка перетинає прямі 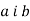 . Чи лежать прямі
. Чи лежать прямі 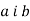 та точка М в одній площині?
та точка М в одній площині?
- Точки M, N, P i Q – середини відрізків BD, CD, AB i AC відповідно, AD=16 см, ВС=18 см. Знайдіть периметр чотирикутника MNQP.
Уроки №6, 7
Природа і життя людини формулює
власні закони мовою математики
Г.Галілей
Фронтальне опрацювання матеріалу
Властивості паралельних прямих. Ознака паралельності прямих у просторі
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 4.17 блоку №1.
- Продовжи речення:
- Властивості основних геометричних фігур виражаються…
- Основними фігурами стереометрії є…
- Якщо дві прямі не мають спільних точок і не лежать на одній площині, то вони…
- Через дві мимобіжні прямі можна провести площину …
- Систему координат на площині увів…
- Єдину площину можна провести через…
- Властивості паралельних прямих на у просторі …
- Скільки середніх ліній в трикутнику, а в трапеції?
- Які взаємні розміщення прямих на площині ви знаєте?
- Сформулюйте ознаку паралельності прямих у просторі.
- Сформулюйте ознаку мимобіжних прямих.
Завдання 2.
Чи правильно що:
- Якщо дві прямі лежать в одній площині, то вони не мимобіжні?
- Якщо дві прямі не перетинаються, то вони паралельні?
- Дві прямі завжди лежать в одній площині?
- Якщо пряма у просторі перетинає одну з двох паралельних прямих, то вона обов’язково перетинає другу паралельну пряму?
Завдання 3.
-
Прямi
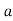 i
i 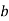 перетинаються. Як можуть бути розташовані прямі
перетинаються. Як можуть бути розташовані прямі 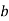 i
i 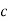 , якщо прямi
, якщо прямi 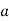 i
i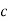 :
:
а) паралельнi;
б) перетинаються;
в) мимобiжнi?
- Прямi a i b паралельнi. Як можуть бути розташовані прямі b i c,якщо прямі a i c:
а) паралельнi;
б) перетинаються;
в) мимобiжнi?
- Прямi a i b мимобiжнi. Як можуть бути розташовані прямі b i c,якщо прямі a i c:
а) паралельнi;
б) перетинаються;
в) мимобiжнi?
- Сформулюйте твердження про дві прямi, що не мають спільних точок, яке:
а) правильне в просторi, але неправильне в площинi;
б) правильне в площинi, але неправильне в просторi.
ІІ. Відпрацювання умінь і навичок, застосування правил
Завдання 4.
- Через точку O перетину діагоналей паралелограма ABCD проведено пряму OK, яка не перетинає його сторін. Доведіть, що прямі OK i BC — мимобіжні.
- Пряма a, що паралельна прямiй b, перетинає площину α. Пряма c паралельна прямiй b. Чи може пряма c лежати в площинi α?
- Ромб AMND і трапеція ABCD з основою ВС не лежать в одній площині. Визначте взаємне розміщення прямих MN i BC. Знайдіть площу ромба, якщо MN=5см, ВС=3 см, а висота ромба дорівнює середній лінії трапеції.
- Сума двох із восьми кутів, які утворились при перетині двох паралельних прямих січною, дорівнює 82°. Знайдіть кожний з восьми кутів.
Завдання 5.
-
Зобразіть куб
 . Серед наведених пар прямих вкажіть: 1) пару паралельних прямих; 2) пару мимобіжних прямих. а) АВ і ВС; б) ВD і
. Серед наведених пар прямих вкажіть: 1) пару паралельних прямих; 2) пару мимобіжних прямих. а) АВ і ВС; б) ВD і 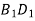 ; в)
; в) 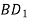 і
і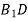 ; г) ВD і
; г) ВD і 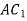 ; д)
; д) 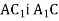 .
.
-
 Зобразіть чотирикутну піраміду SABCD (ABCD – квадрат). Серед наведених пар прямих вкажіть: 1) пару паралельних прямих; б) пару мимобіжних прямих. а) SA і АС; б) SA i АB; в) SC і BD; г) SA і АD; д) ВС і AD.
Зобразіть чотирикутну піраміду SABCD (ABCD – квадрат). Серед наведених пар прямих вкажіть: 1) пару паралельних прямих; б) пару мимобіжних прямих. а) SA і АС; б) SA i АB; в) SC і BD; г) SA і АD; д) ВС і AD.
-
Дано куб
 . Доведіть, що прямі
. Доведіть, що прямі 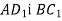 паралельні.
паралельні.
-
Через кінець А відрізка АВ проведено площину α. Через кінець В і точку С цього відрізка проведено паралельні прямі, які перетинають площину α відповідно у точка
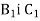 . Знайдіть довжину відрізка АС, якщо
. Знайдіть довжину відрізка АС, якщо 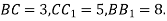
- Доведіть, що середини сторін просторового чотирикутника є вершинами паралелограма.
Завдання 6.
Самостійно виконати індивідуальне завдання, запропоноване вчителем.
 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
-
Через кінці відрізка АВ і його внутрішню точку С проведено паралельні прямі, що перетинають площину
 в точках
в точках 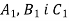 відповідно. Знайдіть
відповідно. Знайдіть 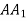 , якщо
, якщо 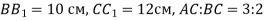 .
.
-
Дано куб
 . Доведіть, що прямі
. Доведіть, що прямі 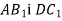 паралельні.
паралельні.
- Відрізок АВ не перетинає площину. Через кінці відрізка АВ проведено паралельні прямі, які перетинають площину у точках А1 та В1. Через точку С, яка ділить відрізок АВ у співвідношенні АС:СВ = 1:2, також проведено пряму, яка паралельна до прямих АА1 та ВВ1. Знайдіть довжину відрізка СС1, якщо АА1 = 2 см та ВВ1=8 см.
Урок №9
«Вивчай усе не заради
марнославства, а заради практичної користі»
Г. Ліхтенберг
Фронтальне опрацювання матеріалу
Паралельність прямої і площини
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 5.18 – 5.23 блоку № 1.
- Усно дай відповідь на питання:
- Як можуть розміщуватись пряма і площина у просторі?
- Дайте означення: прямої, яка належить площині; прямої і площини, які перетинаються; паралельних прямої і площини.
- Як читається ознака паралельності прямої і площини?
Завдання 2.
Усно розв’яжи вправи:
-
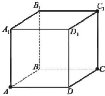 Дано куб
Дано куб  . Встановіть відповідність між заданими прямими (1 – 3) та паралельними їм площинами (А – Г):
. Встановіть відповідність між заданими прямими (1 – 3) та паралельними їм площинами (А – Г):
1 ВС А ![]() Г
Г ![]()
2 AC Б ![]()
-
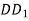 В
В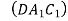
-
Точка А не належить площині
 . Скільки існує прямих, які проходять через точку А і паралельні площині
. Скільки існує прямих, які проходять через точку А і паралельні площині  ?
?
-
Прямі
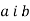 паралельні. Як розміщена пряма
паралельні. Як розміщена пряма 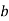 відносно площини
відносно площини  , якщо пряма
, якщо пряма 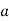 :
:
-
Точка А не належить площині
-
Належить площині
 ;
;
-
Перетинає площину
 ;
;
-
Паралельна площині
 .
.
ІІ. Відпрацювання умінь і навичок, застосування правил
Завдання 3.
Письмово розв’яжи вправи:
- Зобрази трикутну піраміду МАВС. Познач точку К – середину ребра МА. У площині АМС через точку К проведи пряму, паралельну площині МВС.
- Площина β перетинає сторони АВ і АС трикутника АВС в точках K і L відповідно та паралельна стороні ВС. Знайди сторону АВ, якщо ВС : КL = 5 : 3, АК = 15 см.
- Площина α перетинає сторони АВ і АС трикутника АВС у точках М і К відповідно, причому АК : КС = 3 : 2 і МК = 5 см. Знайди довжину відрізка ВС, якщо пряма ВС і площина α паралельні.
- Виконай вправу 4.18 на ст. 264.
- Виконай вправу 4.27 на ст. 265.
Уроки №10, 11
«Як приємно дізнатися,
що ти чогось навчився»
Ж. Мольєр
Фронтальне опрацювання матеріалу
Властивості прямої, паралельної площині
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези блоку № 1.
- Усно дай відповіді на питання:
- Як можуть бути розміщені прямі у просторі?
- Які прямі називаються паралельними, а які – мимобіжними?
- Чи завжди можна провести площину через чотири точки?
- Які ознаки паралельності прямих у просторі ви знаєте?
- Як можуть бути розміщені прямі у просторі відносно площини?
- Яка пряма називається паралельною площині?
- Як можуть бути розміщені дві прямі, якщо одна з них паралельна площині, а інша – перетинає цю площину?
Завдання 2.
Усно виконай вправи:
-
Відомо, що пряма
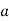 лежить у площині
лежить у площині  . Поставте до кожної умови (А – В) висновок (1 – 3) про розміщення прямих
. Поставте до кожної умови (А – В) висновок (1 – 3) про розміщення прямих 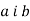 .
.
А) Пряма ![]() перетинає площину
перетинає площину ![]() у точці, що не належить прямій
у точці, що не належить прямій ![]()
Б) Пряма ![]() не перетинає пряму
не перетинає пряму ![]() і належить площині
і належить площині ![]()
В) Пряма ![]() перетинає площину
перетинає площину ![]() у точці, що належить прямій
у точці, що належить прямій ![]()
1) Перетинаються
2) Мимобіжні
3) Паралельні
-
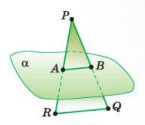 Дано трикутник
Дано трикутник 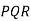 . Площина
. Площина  перетинає сторони
перетинає сторони 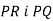 у його серединах – точка А і В відповідно.
у його серединах – точка А і В відповідно. 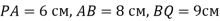 . Поставте у відповідність кожному елементу трикутника його значення.
. Поставте у відповідність кожному елементу трикутника його значення.
А) Довжина ![]()
Б) Довжина ![]()
В) Довжина ![]()
Г) периметр ![]()
Д) периметр ![]()
1) 18 см
2) 46 см
3) 12 см
4) 16 см
5) 23 см
ІІ. Відпрацювання умінь і навичок, застосування правил
Завдання 3.
Письмово виконай вправи:
- У трикутнику АВС відрізок DЕ паралельній стороні АС Знайти:
- АС, якщо ВD = 4, ДЕ = 3, АВ = 12.
- ВЕ, якщо ВD= 3, АВ=6,6; ВС=5,5.
-
АС, якщо
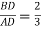 , DE= 15.
, DE= 15.
-
Через кінець А відрізка АВ проведено площину
 , а через кінець В і точку С відрізка АВ проведено паралельні прямі, які перетинають площину
, а через кінець В і точку С відрізка АВ проведено паралельні прямі, які перетинають площину  у точках
у точках 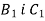 . Знайти:
. Знайти:
-
Через кінець А відрізка АВ проведено площину
-
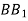 , якщо АС = 3 см, АВ = 6 см,
, якщо АС = 3 см, АВ = 6 см, 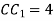 см.
см.
-
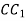 , якщо
, якщо 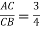 ,
, 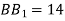 см.
см.
-
Дано трикутник АВС. Площина
 перетинає його сторони АВ і ВС відповідно у їх серединах К і М. Довести, що пряма АС паралельна площині
перетинає його сторони АВ і ВС відповідно у їх серединах К і М. Довести, що пряма АС паралельна площині  .
.
- Точка М не належить площині прямокутника АВСD. Довести, що пряма АВ паралельна площині МDC.
-
Площина
 перетинає сторони АВ і АС трикутника АВС у точка М і К так, що
перетинає сторони АВ і АС трикутника АВС у точка М і К так, що 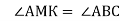 . Довести, що пряма ВС паралельна площині
. Довести, що пряма ВС паралельна площині  .
.
-
Дано трикутник АВС. Площина
 , яка паралельна прямій АС, перетинає сторону АВ у точці К, а сторону ВС – у точці М. Довести, що пряма КМ паралельні прямій АС.
, яка паралельна прямій АС, перетинає сторону АВ у точці К, а сторону ВС – у точці М. Довести, що пряма КМ паралельні прямій АС.
-
Дано трикутник АВС. Площина
 , яка паралельна прямій АВ, перетинає сторону АС у точці
, яка паралельна прямій АВ, перетинає сторону АС у точці 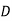 , а сторону АВ – у точці Е. Обчислити:
, а сторону АВ – у точці Е. Обчислити:
-
Дано трикутник АВС. Площина
- АВ, якщо DC = 8 см, АС = 24 см, АE = 6 см.
-
АE, якщо
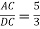 ,АВ = 15 см.
,АВ = 15 см.
 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
-
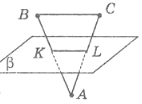 У трикутнику АВС
У трикутнику АВС 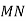 – середня лінія. Через пряму АС проведено площину
– середня лінія. Через пряму АС проведено площину  , яка не збігається з площиною АВС. Доведіть, що
, яка не збігається з площиною АВС. Доведіть, що 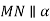 .
.
- Площина β перетинає сторони АВ і АС трикутника АВС в точках К і L відповідно та паралельна стороні ВС. Знайдіть сторону АС, якщо ВС : КL = 5 : 1, АL = 4 см.
-
Дано трикутник АВС. Площина
 , яка паралельна прямій ВС, перетинає сторону АВ у точці
, яка паралельна прямій ВС, перетинає сторону АВ у точці 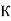 , а сторону АC – у точці М. Обчисли АC, якщо АК = 4 см, АВ = 7 см, МС = 12 см.
, а сторону АC – у точці М. Обчисли АC, якщо АК = 4 см, АВ = 7 см, МС = 12 см.
Урок №13
«Серед усіх наук, які відкривають шлях до пізнання законів
природи, найвеличнішою є математика»
С. Ковалевська
Внутрішньопредметне узагальнення матеріалу
Аксіоми стереометрії. Паралельність прямих у просторі. Паралельність прямої і площини
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори блок № 1.
- Письмово дай відповідь на питання, запропоновані вчителем.
Завдання 2.
Усно виконай вправи:
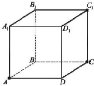
-
Дано куб
 . Серед наведених пар
. Серед наведених пар
прямих вкажи пару: а) паралельних прямих; б) мимобіжних прямих.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
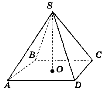
- Дано чотирикутну піраміду SABCD. Серед наведених прямих
вкажи пару: а) паралельних прямих; б) мимобіжних прямих.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
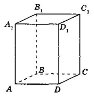
-
Дано прямокутний паралелепіпед
 . Визнач
. Визнач
взаємне розміщення прямих ![]() .
.
|
А |
Б |
В |
Г |
Д |
|
Паралельні |
Мимобіжні |
Паралельні або перетинаються |
Мимобіжні або перетинаються |
Паралельні або мимобіжні |
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 3.
Письмово виконай вправи:
-
Через кінець А відрізка АВ проведено площину α. Через кінець В і точку С відрізка АВ проведено паралельні прямі, які перетинають площину α в точках
 відповідно. Знайти
відповідно. Знайти 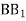 , якщо
, якщо 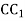 = 30 см, АС : АВ = 3 : 14.
= 30 см, АС : АВ = 3 : 14.
- Дано трикутник МРК. Площина α, що паралельна прямій МР, перетинає сторону МК у точці А, а сторону РК – у точці В. Знайди МР, якщо АВ = 25 см, АК : АМ = 5 : 2.
- Дано трикутник АВС. Площина, яка паралельна прямій ВС, перетинає сторону АВ у точці К, а сторону АС – у точці М. Обчислити АС, якщо АК = 8 см, АВ = 14 см, МС = 24 см.
Тема №2. Паралельність площин
Урок №1

Паралельність площин
…щоб слухало мудрості вухо твоє,
своє серце прихилиш до розуму
Приповісті Соломонові 2:2
Питання
- Паралельність площин.
- Властивості паралельних площин.
- Паралельне проектування і його властивості.
- Зображення фігур у стереометрії.
Література
Істер О.С. Математика: (алгебра і початки аналізу та геометрія, рівень стандарту): Підручник для 10 класу закладів загальної середньої освіти. Київ: Генеза, 2018 рік, розділ Геометрія, §§3, 5, стор. 248 – 258, 268 – 276.
|
1. Паралельність площин |
|||
|
1.1 |
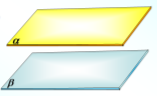
Дві площини називаються паралельними, якщо вони не мають спільних точок.
|
|
|
|
1.2 |
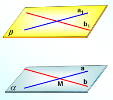
Теорема (ознака паралельності площин) Якщо дві прямі, що перетинаються однієї площини, відповідно паралельні двом прямим, які перетинаються, другої площини, то ці площини паралельні. |
Якщо |
|
|
2. Властивості паралельних площин |
|||
|
2.3
|
1.Теорема (основна властивість паралельних площин) Через точку, яка не лежить у площині, можна провести площину, паралельну даній площині, і тільки одну. |
||
|
2.4 |
2.Теорема Якщо дві паралельні площини перетнути третьою, то прямі їх перетину паралельні. |
Якщо
то
|
|
|
2.5 |
3. Теорема Відрізки паралельних прямих, кінці яких належать двом паралельним площинам, рівні між собою. |
Якщо
то
|
|
|
2.6 |
Взаємне розміщення площин:
1) мають спільну точку – перетинаються по прямій –
2) не мають спільних точок – паралельні – |
||
|
3. Паралельне проектування і його властивості |
|||
|
3.7 |
Для зображення фігур у просторі користуються паралельним проектуванням: проектування здійснюється паралельними прямими.
|
α – площина проекцій,
|
|
|
3.8 |
Основні властивості паралельного проектування
|
||
|
4. Зображення фігур у стереометрії |
|||
|
4.9 |
Паралелограм, квадрат, прямокутник, ромб зображуються паралелограмом.
|
|
|
|
Всі види трикутників зображуються довільним трикутником.
|
|
|
|
|
Коло зображується еліпсом
|
|
|
|
|
Всі види трапецій зображуються довільною трапецією |
|
|
|
Урок №2
«Не роби ніколи того, що не знаєш.
Але вчись усьому, що потрібно знати,
і тоді будеш вести спокійне життя»
Піфагор
Фронтальне опрацювання матеріалу
Взаємне розміщення двох площин у просторі
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
Повторивши тези 1.1 – 2.6 блоку № 2, дай відповіді на питання:
- Яким може бути взаємне розміщення двох площин у просторі? (Опиши, покажи, обґрунтуй).
- У якому випадку дві площини називаються паралельними? Такими, що перетинаються?
- Як через дану точку провести площину, паралельну даній площині?
- Сформулюй ознаку паралельності площин.
- Чи має істотне значення в ознаці паралельності площин те, що дві прямі перетинаються?
- Сформулюй теорему про перетин двох паралельних площин третьою площиною.
- Сформулюй теорему про відрізки паралельних прямих, які містяться між паралельними площинами.
Завдання 2.
Побудуй куб ![]() . Назви площину, паралельну:
. Назви площину, паралельну:
-
площині
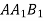 ;
;
-
площині
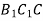 ;
;
-
площині
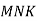 , де М – середина AD, N–середина DC, K–середина
, де М – середина AD, N–середина DC, K–середина 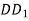 .
.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Письмово виконайте вправи:
- Точка D не лежить у площині трикутника АВС. Точки М, К, Р – відповідно середини відрізків АВ, АС і AD. Довести, що площини ВСD і MKP паралельні.
-
Дано куб
 . Довести, що площини
. Довести, що площини 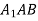 i
i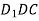 паралельні.
паралельні.
-
Дві паралельні площини
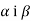 перетинають сторону ВА кута АВС у точка Di
перетинають сторону ВА кута АВС у точка Di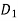 , а сторону ВС – у точках Е і
, а сторону ВС – у точках Е і 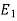 . Як розташовані прямі
. Як розташовані прямі 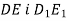 ? Відповідь обґрунтувати. Знайти DE, якщо BD= 3 cм,
? Відповідь обґрунтувати. Знайти DE, якщо BD= 3 cм, 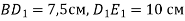 .
.
Урок №3
«Не роби ніколи того, що не знаєш.
Але вчись усьому, що потрібно знати,
і тоді будеш вести спокійне життя»
Піфагор
Фронтальне опрацювання матеріалу
Ознака паралельності площин
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 1.2 блоку № 2.
- Усно дати відповіді на питання:
- Яким може бути взаємне розміщення двох площин у просторі? (Опиши, покажи, обґрунтуй).
- У якому випадку дві площини називаються паралельними? Такими, що перетинаються?
- Сформулюй ознаку паралельності площин.
Завдання 2.
Усно виконати вправи, стор. 271 підручника: 5.4, 5.6.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Письмово виконати вправи, стор. 272 підручника: 5.14, 5.16, 5.30, 5.42.
Урок №4
«Хто стереже уста свої і язика
свого, той береже від лиха душу свою»
Приповісті Соломонові 20:23
Фронтальне опрацювання матеріалу
Властивості паралельних площин
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 1.1 – 2.6 блоку № 2.
- Дайте відповіді на питання графічного диктанту, запропонованого вчителем.
![]()
![]() Якщо твердження правильне, ставите знак , якщо неправильне – знак .
Якщо твердження правильне, ставите знак , якщо неправильне – знак .
Завдання 2.
- Знайдіть в кабінеті модель двох паралельних площин, які перетинаються третьою площиною.
- Покажіть лінії перетину цих площин третьою площиною.
- Що можна сказати про взаємне розташування цих прямих ?
- Знайдіть в кабінеті модель двох паралельних площин, які перетинають паралельні прямі.
- Що можна сказати про відрізки, які відтинають паралельні площини від паралельних прямих ?
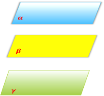
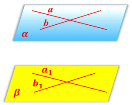
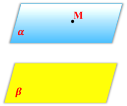
Завдання 3.
Дивлячись на малюнки, скажіть, якому правилу вони відповідають або сформулюйте свою правило.

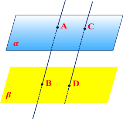
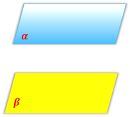
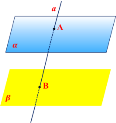
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 4.
- Площини α і ß паралельні. У площині α вибрано точки M і N, а в площині ß – точки M1 і N1 такі, що прямі ММ1 і NN1 паралельні. Знайти довжини відрізків NN1 і М1N1, якщо МN = 5см, ММ1 = 6см.
-
Сторона АВ трикутника АВС лежить у площині α. Площина β паралельна площині α і перетинає сторони АС і ВС у точках
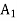 і
і 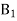 відповідно. Знайдіть довжину відрізка
відповідно. Знайдіть довжину відрізка 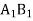 , якщо АВ = 12 см,
, якщо АВ = 12 см, 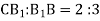 .
.
-
Побудуйте переріз прямокутного паралелепіпеда
 площиною, що проходить через точки
площиною, що проходить через точки 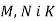 , які належать відповідно ребрам
, які належать відповідно ребрам 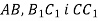 .
.
Урок №5
«Людина, що не знає математики, не здатна ні до яких інших наук. Більш того, вона навіть не здатна оцінити рівень свого невігластва, а тому не шукає від нього ліки»
Роджер Бекон
Фронтальне опрацювання матеріалу
Паралельне проектування, його властивості. Зображення плоских і просторових фігур у стереометрії
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 3.7 – 4.9 блоку № 2.
- Продовжте речення:
- Паралельне проектування – це…
- Проекцією правильного трикутника на площину є…
- Проекцією тупокутного трикутника на площину є…
- Проекцією прямокутної трапеції на площину є…
- Проекцією ромба на площину є…
- Проекцією кола на площину є…
- Проекцією правильного шестикутника на площину є…
- За допомогою чого здійснюється паралельне проектування?
- Назвіть основні властивості паралельного проектування.
Завдання 2.
Виконайте усно:
- Які геометричні фігури можуть бути паралельними проекціями: 1) прямої; 2) двох паралельних прямих; 3) трикутника?
- Чи можна при паралельному проектуванні прямокутника отримати: 1 )квадрат; 2) трапецію?
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
- Усно виконати вправи, запропоновані вчителем у презентації.
- Поділіться на 3 групи. За допомогою ліхтариків у ваших мобільних телефонах, виконайте практичне завдання, запропоноване вчителем у презентації.
Завдання 4.
-
Точки
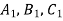 є паралельними проекціями відповідно точок А, В, С, які лежать на одній прямій (точка В лежить між точками А і С). Знайдіть відрізок
є паралельними проекціями відповідно точок А, В, С, які лежать на одній прямій (точка В лежить між точками А і С). Знайдіть відрізок 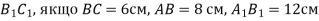 .
.
-
Трикутник
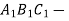 проекція рівнобедреного трикутника АВС (АВ=АС). Побудувати проекцію висоти, бісектриси та медіани трикутника, проведеної з вершини В.
проекція рівнобедреного трикутника АВС (АВ=АС). Побудувати проекцію висоти, бісектриси та медіани трикутника, проведеної з вершини В.
-
Дано проекції вершин трикутника АВС на площину. Побудуйте проекцію бісектриси кута В, якщо
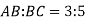 .
.
Урок №6
«Новий Заповіт є найвеличнішою книгою
тепер і в майбутньому для всього світу»
Чарльз Діккенс
Фронтальне опрацювання матеріалу
Паралельність площин. Паралельне проектування
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези блоку №2.
- Дайте відповіді на питання:
- Які дві площини називаються паралельними?
- Сформулюйте ознаку паралельності площин.
- Як можуть розміщуватись площини у просторі?
- Сформулюйте основну властивість паралельності площин.
- Якщо дві паралельні площини перетнути третьою, то…
- Відрізки паралельних прямих, що відтинаються паралельними площинами…
- Що називають паралельним проектуванням? Які його властивості?
- Як у просторі зображають правильний трикутник; квадрат; рівнобічну трапецію?
Завдання 2.
Усно виконайте вправи:
- Дано дві паралельні площини α і β. Визначте, скільки в площині α існує прямих, які паралельні площині β.
|
А |
Б |
В |
Г |
Д |
|
Жодної |
Тільки одна |
Жодної або нескінченна множина |
Жодної або одна |
Нескінченна множина |
- Вкажіть, яка з наведених фігур не може бути проекцією прямокутника:
|
А |
Б |
В |
Г |
Д |
|
Квадрат |
Паралелограм |
Прямокутник |
Трапеція |
Ромб |
- Вкажіть, яка з наведених фігур може бути паралельною проекцією основ трапеції.
|
А |
Б |
В |
Г |
Д |
|
Одна точка |
Дві точки |
Одна пряма |
Два відрізки, які перетинаються |
Дві прямі |
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
-
Зобразіть куб
 . Яка площина паралельна площині
. Яка площина паралельна площині 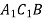 ?
?
-
Трикутник
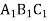 – проекція рівнобедреного трикутника АВС (АВ = АС). Побудувати проекцію висоти трикутника, проведеної з вершини А.
– проекція рівнобедреного трикутника АВС (АВ = АС). Побудувати проекцію висоти трикутника, проведеної з вершини А.
-
Паралельні площини α і β перетинають сторони кута АВС в точках
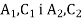 відповідно. Знайдіть
відповідно. Знайдіть 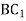 , якщо
, якщо 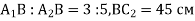 .
.
-
Через точку О, що лежить між паралельними площинами, проведено прямі
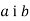 , які перетинають площину α відповідно у точках
, які перетинають площину α відповідно у точках 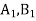 , а площину β – у точках
, а площину β – у точках 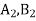 . Обчислити
. Обчислити 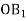 , якщо
, якщо 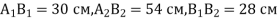 .
.
 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
-
Зобразіть куб
 . Яка площина паралельна площині
. Яка площина паралельна площині 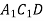 ?
?
-
Паралелограм
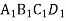 – проекція квадрата АВСD. Побудувати проекцію перпендикуляра, проведеного із точки перетину діагоналей квадрата до сторони AD.
– проекція квадрата АВСD. Побудувати проекцію перпендикуляра, проведеного із точки перетину діагоналей квадрата до сторони AD.
-
Паралельні площини α і β перетинають сторони кута АВС в точках
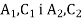 відповідно. Знайдіть
відповідно. Знайдіть 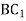 , якщо
, якщо 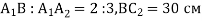 .
.
-
Два промені з початком у точці О перетинають одну з паралельних площин відповідно у точках
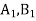 , а другу – у точках
, а другу – у точках 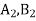 . Обчислити
. Обчислити 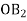 , якщо
, якщо 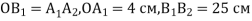 .
.
Урок №8
«Не роби ніколи того, що не знаєш.
Але вчись усьому, що потрібно знати,
і тоді будеш вести спокійне життя»
Піфагор
Внутрішньопредметне узагальнення матеріалу
Паралельність площин
І. Узагальнення теоретичних знань
Завдання 1.
- Повторіть блок № 2.
- Письмово дайте відповіді на питання, запропоновані вчителем.
ІІ. Узагальнення практичних умінь та навичок
Завдання 2.
Усно виконайте вправи:
-
Намалюйте прямокутний паралелепіпед
 . Вкажіть площину, яка паралельна площині
. Вкажіть площину, яка паралельна площині 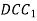 .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
- Вкажіть, яка з наведених фігур може бути паралельною проекцією рівнобічної трапеції.
|
А |
Б |
В |
Г |
Д |
|
Ромб |
Квадрат |
Довільна трапеція |
Прямокутник |
Довільний трикутник |
- Зазначте, як розміщені площина паралелограма АВСD і площина α, якщо діагоналі паралелограма паралельні площині α.
|
А |
Б |
В |
Г |
Д |
|
Паралельні |
Перетинаються |
Збігаються |
Збігаються або перетинаються |
Паралельні або збігаються |
Завдання 3.
Письмово виконайте вправи:
-
Трикутник
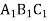 – проекція рівнобедреного трикутника АВС (АВ = АС). Побудувати проекцію перпендикуляра, проведеного із середини бічної сторони до основи трикутника.
– проекція рівнобедреного трикутника АВС (АВ = АС). Побудувати проекцію перпендикуляра, проведеного із середини бічної сторони до основи трикутника.
-
Дві паралельні площини α і β перетинають сторону АВ кута ВАС у точках D і
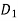 , а сторону AC – у точках E і
, а сторону AC – у точках E і 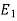 . Знайти DE, якщо
. Знайти DE, якщо 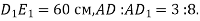
- Дано дві паралельні площини α і β. Точки А і В належать площині α, а точки С і D – площині β. Відрізки АD і ВС перетинаються в точці S. Знайдіть довжину відрізка СD, якщо АВ = 20 см, АS = 4 см, DS = 2 см.
-
Два промені з початком у точці О перетинають одну з паралельних площин відповідно у точках
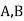 , а другу – у точках
, а другу – у точках 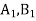 . Обчислити
. Обчислити 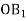 , якщо
, якщо 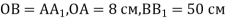 .
.
Тема №3. перпендикулярність прямих у просторі. Перпендикулярність прямої і площини
Урок №1

«Геометрія є пізнання всього існуючого»
Платон
Перпендикулярність прямих у просторі. Перпендикулярність прямої і площини
Питання
- Перпендикулярність прямих, прямої і площини.
- Перпендикуляр і похила до площини.
- Теорема про три перпендикуляри.
- Залежність між паралельністю і перпендикулярністю прямих і площин.
Література
Істер О.С. Математика: (алгебра і початки аналізу та геометрія, рівень стандарту): Підручник для 10 класу закладів загальної середньої освіти. Київ: Генеза, 2018 рік, розділ Геометрія, §§6, 7, стор. 278 – 297.
|
1. Перпендикулярність прямих, прямої і площини |
||
|
1.1 |
Дві прямі, які перетинаються під прямим кутом, називаються перпендикулярними прямими. |
|
|
1.2 |
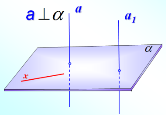
Пряма, яка перетинає площину, називають перпендикулярною до площини, якщо вона перпендикулярна до кожної прямої, яка лежить у площині і проходить через точку перетину. |
|
|
1.3 |
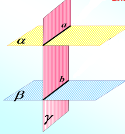
Теорема (ознака перпендикулярності прямої і площини) Якщо пряма, яка перетинає площину, перпендикулярна до двох прямих цієї площини, що проходять через точку перетину, то вона перпендикулярна до площини. |
|
|
2. Властивості взаємно перпендикулярних прямих і площин |
||
|
2.4 |
Теорема (про паралельні прямі та перпендикулярну площину) Якщо площина перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна і до другої
|
|
|
2.5 |
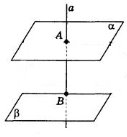
Теорема (про паралельні площини і перпендикулярну пряму) Якщо пряма перпендикулярна до однієї з паралельних площин, то вона перпендикулярна і до другої
|
|
|
3. Перпендикуляр і похила |
||
|
3.6 |
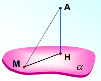
Перпендикуляром, проведеним з даної точки до даної площини, називається відрізок, що сполучає дану точку з точкою площини і лежить на прямій, перпендикулярній до площини. |
АH – перпендикуляр H – основа перпендикуляра АM – похила M – основа похилої HM – проекція похилої |
|
3.7 |
Похилою, проведеною з даної точки до даної площини, називають будь-який відрізок, який сполучає цю точку з точкою площини і не є перпендикуляром. |
|
|
3.8 |
Відрізок, який сполучає основи перпендикуляра і похилої, називають проекцією похилої на площину. |
|
|
3.9 |
Теорема 1) Довжина перпендикуляра, проведеного з точки до площини, менша за довжину будь-якої похилої, проведеної з цієї самої точки до площини; 2) проекції рівних похилих рівні і, навпаки, похилі, що мають рівні проекції, рівні; 3) з двох похилих більша та, проекція якої більша. |
|
|
4. Теорема про три перпендикуляри |
||
|
4.10 |
Теорема ( про три перпендикуляри) Якщо пряма, проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна і до самої похилої. |
|
|
4.11 |
Теорема (обернена до теореми про три перпендикуляри) Якщо пряма на площині перпендикулярна до похилої, то вона перпендикулярна і до проекції похилої. |
|
Урок №2
«З усіх утрат втрата часу найтяжча»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Перпендикулярність прямих у просторі. Перпендикулярність прямої і площини
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 1.1. – 2.5 блоку № 3.
- Усно дайте відповіді на питання:
- Які прямі в просторі називаються перпендикулярними?
- Сформулюйте означення прямої, перпендикулярної до площини.
- Сформулюйте ознаку перпендикулярності прямої і площини.
-
Сформулюйте властивості взаємно перпендикулярних прямих і площин.
- Перегляньте інформацію, надану вчителем у презентації.
ІІ. Відпрацювання умінь і навичок розв’язування вправ і задач
Завдання 2.
Усно виконайте вправи, стор. 282 підручника: 6.1, 6.2.
Завдання 3.
Письмово виконайте вправи, стор. 283 підручника: 6.11, 6.35.
Завдання 4.
Письмово виконати вправи:
-
В трикутнику АВС дано
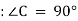 , АС = 6 см, ВС = 8 см, СМ – медіана. Через вершину С проведено пряму СК, перпендикулярну до площини трикутника АВС, причому СК = 12 см. Знайдіть КМ.
, АС = 6 см, ВС = 8 см, СМ – медіана. Через вершину С проведено пряму СК, перпендикулярну до площини трикутника АВС, причому СК = 12 см. Знайдіть КМ.
-
Через вершину А трикутника АВС проведено площину, яка паралельна ВС,
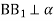 ,
, 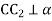 , СС1 = 4, АС1 =
, СС1 = 4, АС1 =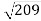 , АВ1 =
, АВ1 = 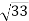 ,
, 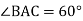 . Знайдіть ВС.
. Знайдіть ВС.
Урок №3
«Якщо ти змудрів – то для себе змудрів»
Книга приповістей Соломонових 9:12
Фронтальне опрацювання матеріалу
Ознака перпендикулярності прямої і площини
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 1.1 – 2.5 блоку № 3.
- Дайте відповіді на питання:
- Які прямі у просторі називаються перпендикулярними?
- Які пряма і площина у просторі називаються перпендикулярними?
- Сформулюйте ознаку перпендикулярності прямої і площини.
- Укажіть в оточуючому просторі моделі площин і прямих, які перпендикулярні.
 Завдання 2.
Завдання 2.
-
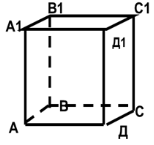
Назвіть усі ребра куба, які перпендикулярні до ребра
-
Доведіть, що пряма, яка проходить через вершину
 куба
куба
і центр грані ![]() , перпендикулярна до прямої
, перпендикулярна до прямої ![]() .
.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Виконати усно вправи за готовими малюнками, запропоновані вчителем.
Завдання 4.
- Через точку О перетину діагоналей паралелограма АВСD проведено пряму ОМ так, що МА = МС, МВ = МD. Доведіть, що пряма МО перпендикулярна до площини паралелограма.
-
В трикутнику АВС сума кутів А і В дорівнює 900. Пряма ВD перпендикулярна до площини АВС. Доведіть, що
 .
.
- АВСD – прямокутник. Відрізок АЕ перпендикулярний до площини АВС. ВЕ = 15 см, ЕС = 24 см, ЕD = 20 см. Доведіть, що трикутник ЕDС прямокутний і знайдіть АЕ.
Урок №4
«Більше думай і тоді вирішуй»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Перпендикуляр і похила
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 1.1 – 3.9 блоку № 3.
- Усно дайте відповідь на питання:
- Сформулюйте означення перпендикулярних прямих.
- Дайте означення прямої, перпендикулярної до площини.
- Сформулюйте ознаку перпендикулярності прямої та площини.
- Що називають перпендикуляром до даної прямої у просторі?
- Що називають похилою?
- Що називають проекцією похилої?
- Які властивості мають перпендикуляр і похила?
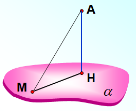
Завдання 2.
Користуючись рисунком, дайте відповідь на питання:
- Як називають відрізок АН?
- Як називають відрізок АМ?
- Як називають точку Н, точку М?
- Як називають відрізок НМ?
- Скільки перпендикулярів можна провести з даної точки до даної площини?
- Скільки похилих можна провести з даної точки до даної площини?
- Скільки рівних похилих можна провести з даної точки до даної площини?
- Якщо до площини з однієї точки проведені перпендикуляр і похила, то що більше: перпендикуляр чи похила?
- Якщо похилі, проведені з однієї точки до даної площини, рівні, то що можна сказати про їх проекції?
- Якщо проекції похилих різні, то яка похила буде більша?
ІІ. Відпрацювання умінь і навичок розв’язування вправи
Завдання 3.
Усно виконати вправи:
- З точки М, що не належить площині, проведені дві похилі МВ і МА та перпендикуляр МО.
- Яка точка є проекцією точки М?
-
 Назвіть відрізок, довжина якого дорівнює відстані від точки М до площини α.
Назвіть відрізок, довжина якого дорівнює відстані від точки М до площини α.
- Якщо МА = 9 см, МВ = 12 см, то яка проекція буде більша?
- Якщо ОА = 3 см, ОВ = 1 см, то яка похила більша?
-
Якщо МА : МВ = 5 : 6, то яка проекція буде менша?
- Дано куб АВСDA'B'C'D'. Укажіть проекцію діагоналі B'D на площину:
1) АВС; 2) ВВ'С'
Завдання 4.
Письмово виконати вправи:
- Знайдіть довжину похилої, якщо довжина перпендикуляра дорівнює 6 см, а проекції похилої на площину – 8 см.
-
З вершини A квадрата АВСD проведено перпендикуляр KA до його площини. Знайдіть відстань CK, якщо KA дорівнює 6 см, а сторона квадрата – 4
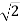 см.
см.
- З точки до площини проведені дві похилі, які дорівнюють 10 см і 17 см, а їх проекції відносяться, як 2 : 5. Знайдіть відстань від даної точки до площини.
Урок №5
«Якщо ти змудрів – то для себе змудрів»
Книга приповістей Соломонових 9:12
Фронтальне опрацювання матеріалу
Перпендикулярність прямої і площини. Перпендикуляр і похила
І. Робота над засвоєнням понять, термінів і правил
Завдання 1
- Повторити тези 1.1 – 3.9 блоку № 3.
- Усно дати відповідь на питання:
- Які прямі називаються перпендикулярними?
-
 Яка пряма називається перпендикулярною до площини?
Яка пряма називається перпендикулярною до площини?
- Сформулювати ознаку перпендикулярності прямої і площини.
- Дати означення перпендикуляра до площини, похилої, проекції похилої.
- Сформулювати властивості перпендикулярів і похилих.
Завдання 2.
Усно виконати вправи:
-
Користуючись зображенням куба
 , вкажіть пряму, яка перпендикулярна до прямої BD.
, вкажіть пряму, яка перпендикулярна до прямої BD.
|
А |
Б |
В |
Г |
Д |
|
АВ |
ВС |
|
АС |
ВD |
-
Користуючись зображенням куба
 на дошці, вкажіть площину, яка перпендикулярна до прямої AD.
на дошці, вкажіть площину, яка перпендикулярна до прямої AD.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
З точки А до площини проведено дві похилі АВ і АС та перпендикуляр АO. Відомо,що
 . Який з поданих записів є правильним?
. Який з поданих записів є правильним?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
ІІ. Відпрацювання умінь і навичок розв’язування вправи
Завдання 3.
Письмово виконати вправи:
- Встановіть відповідність між умовою твердження (1 – 4) та його висновком (А – Д) так, щоб утворилось істинне твердження.
1 Якщо з точки проведено дві рівні похилі, то А більша похила має більшу проекцію
2 Якщо з точки проведено дві різні похилі, то Б більша похила має меншу проекцію
3 Якщо з точки проведено перпендикуляр і похилу, то В вони мають рівні проекції
4 Якщо з точки проведено два перпендикуляри, то Г вони збігаються
Д похила більша від проекції
похилої
- Відрізок МА перпендикулярний до площини прямокутника АВСD, у якого АВ = 6 см, ВС = 8 см. Знайдіть відстань від точки М до точки А, якщо МС = 26 см.
-
З точки А до площини проведено дві похилі АВ і АС та перпендикуляр АО. Знайдіть АВ і АС, якщо АВ : АС =
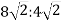 , ВО = 8 см, СО = 4 см.
, ВО = 8 см, СО = 4 см.
-
З точки А до площини проведено дві похилі АВ і АС та перпендикуляр АО. Знайдіть ВО і СО, якщо ВО – СО = 3 см,
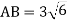 см, АС =3
см, АС =3 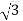 см.
см.
 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
- Відрізок МА перпендикулярний до площини прямокутника АВСD, у якого АВ = 6 см, ВС = 8 см. Знайдіть відстань від точки М до точки С, якщо МА = 24 см.
-
З точки А до площини проведено дві похилі АВ і АС та перпендикуляр АО. Знайдіть ОВ і СD, якщо ВО – СО = 2 см,
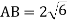 см, АС =
см, АС = 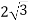 см.
см.
Уроки №7, 8
«Хто думає про науку, той любить її,
а хто її любить, той ніколи не перестає вчитися»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Теорема про три перпендикуляри
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 1.1 – 4.11 блоку № 3.
- Усно дайте відповіді на питання:
- Які прямі називаються перпендикулярними?
- Які пряма і площина називаються перпендикулярними?
- Сформулюйте ознаку перпендикулярності прямої і площини.
- Дайте визначення перпендикуляра і похилої.
- Сформулюйте властивості перпендикуляра і похилої.
- Сформулюйте теорему про три перпендикуляра.
- Сформулюйте теорему, обернену до теореми про три перпендикуляри.
Завдання 2.
Усно виконати вправи:
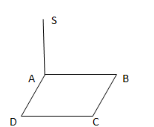
- До площини квадрата ABCD проведено перпендикуляр SA (див. рисунок). Вкажіть пряму, яка перпендикулярна до прямої SD.
|
А |
Б |
В |
Г |
Д |
|
AC |
DB |
BC |
CD |
SA |
-
Зобразіть куб
 , О – центр грані АВСD, вкажіть пряму, яка перпендикулярна до прямої
, О – центр грані АВСD, вкажіть пряму, яка перпендикулярна до прямої 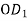 .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
На рисунку зображено куб
 . Вкажіть проекцію похилої
. Вкажіть проекцію похилої 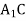 на площину
на площину 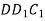 .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Виконайте письмово вправи:
-
В трикутнику кут С прямий, кут А дорівнює 600, AС=12см.
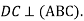
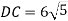 . Знайдіть відстань: 1) від точки С до прямої АВ, 2) від точки D до прямої АВ.
. Знайдіть відстань: 1) від точки С до прямої АВ, 2) від точки D до прямої АВ.
-
Через вершину прямого кута С рівнобедреного прямокутного трикутника АВС проведено пряму СМ, яка перпендикулярна до його площини. Знайдіть відстань від точки М до прямої АВ, якщо АС = 4 см, а
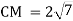 см.
см.
- З точки М проведено перпендикуляр МВ до площини прямокутника АВСD. Доведіть, що трикутники АМD і МСD прямокутні.
Завдання 4.
Виконати письмово вправи
-
До площини квадрата АВСD проведено перпендикуляр SB; SВ = 24 см, АС =
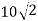 см. Знайдіть відстань від точки S до прямих AD, СD.
см. Знайдіть відстань від точки S до прямих AD, СD.
-
Дано правильний трикутник АВС зі стороною
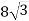 см. Точка S рівновіддалена від усіх сторін цього трикутника. Знайдіть відстань від точки S до площини АВС, якщо відстань від точки S до сторони ВС дорівнює 5 см.
см. Точка S рівновіддалена від усіх сторін цього трикутника. Знайдіть відстань від точки S до площини АВС, якщо відстань від точки S до сторони ВС дорівнює 5 см.
-
Дано правильний трикутник АВС зі стороною
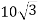 см. Точка S рівновіддалена від усіх сторін цього трикутника. Знайдіть відстань від точки S до сторони АВ, якщо відстань від точки S до площини АВС дорівнює
см. Точка S рівновіддалена від усіх сторін цього трикутника. Знайдіть відстань від точки S до сторони АВ, якщо відстань від точки S до площини АВС дорівнює 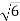 см.
см.
Урок №9
«Батько і мати дали тобі життя й живуть
заради твого щастя. Бережи їх здоров’я і спокій»
В. Сухомлинський
Фронтальне опрацювання матеріалу
Теорема про три перпендикуляри
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези блоку № 3.
- Зіграйте в інтелектуальне лото, запропоноване вчителем.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
Письмово розв’яжіть задачі, заповнивши пропуски:
-
 З деякої точки до площини проведені перпендикуляр і 2 похилі. Визначити довжину перпендикуляра, якщо похилі відносяться як 3:4, а їх проекції дорівнюють відповідно 9 см і 16 см.
З деякої точки до площини проведені перпендикуляр і 2 похилі. Визначити довжину перпендикуляра, якщо похилі відносяться як 3:4, а їх проекції дорівнюють відповідно 9 см і 16 см.
Розв’язування
![]()
АС, АD-_____________;
ВС і ВD- їх ________________ відповідно;
Так як АС:АD=__________, то
Нехай АС=______см, АD=______см,
де х- коефіцієнт пропорційності.
Оскільки більшій похилій відповідає _____________ проекція, то
ВС=_____см, ВD=_____см.
З ∆ АВD (<АВD=_____°) за теоремою Піфагора:
АВ2=_______-________, АВ2=_______-________
Аналогічно, з ∆ АВС: АВ2=_______-________, АВ2=_______-________
Складаємо рівняння:___________=____________
________________________________
________________________________
Тоді АВ2=______________________
АВ=±√_______=±_______(-______ не задовольняє умову задачі).
Відповідь: довжина перпендикуляра _____см.
-
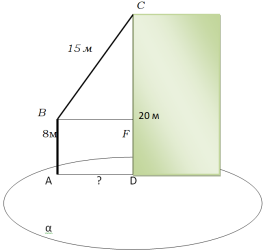 Телефонний провід завдовжки 15 м протягнуто від телефонного стовпа, де він прикріплений на висоті 8 м від поверхні Землі, до будинку, де його закріпили на висоті 20 м. Знайдіть відстань між будинком і стовпом, вважаючи, що провід не провисає.
Телефонний провід завдовжки 15 м протягнуто від телефонного стовпа, де він прикріплений на висоті 8 м від поверхні Землі, до будинку, де його закріпили на висоті 20 м. Знайдіть відстань між будинком і стовпом, вважаючи, що провід не провисає.
Розв’язування
Математична модель поверхні Землі - площина ____,
а відстані 8 м і 20 м від поверхні Землі – прямі, що ___ площині ___.
За властивістю прямих і площин:
АВ ____СD.
Проведемо BF___AD, тоді BF=____
і ∆BCF=_________________(<BFC=____°)
CF=____________.
За теоремою _____________: BF2=________________________________
BF=±√ ____=±_____ (____ не задовольняє умову задачі).
Відповідь: відстань між будинком і стовпом _____м.
- Над квадратною будівлею розміром 12 м×12 м потрібно виготовити дах, найвища точка якої знаходиться на висоті 3 м над основою даху. Якою повинна бути довжина основних балок ?
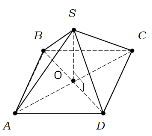
Розв’язування
Аналіз умови задачі:
Всі вершини квадрата повинні знаходитися на однаковій відстані від найвищої точки даху.
Тому маємо математичну модель:
OS ![]() площині квадрата, SD- похила, OD-її _______________
площині квадрата, SD- похила, OD-її _______________
Діагональ квадрата BD=_________ м, ВО=![]() =____ м
=____ м
З ∆SOD (<______=90°) за теоремою ________________:
SD2=22+ ______=_______________________
SD=±√_______=±_____ (____ не задовольняє умову задачі).
Відповідь: довжина кожної основної балки ____ м.
-
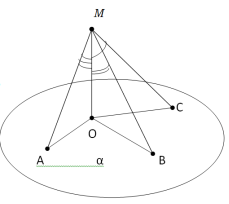 З точки М, що міститься від площини α на відстані МО=4, проведені до цієї площини похилі МА, МВ і МС під кутами 30°, 45° і 60° відповідно до прямої МО, МО
З точки М, що міститься від площини α на відстані МО=4, проведені до цієї площини похилі МА, МВ і МС під кутами 30°, 45° і 60° відповідно до прямої МО, МО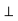 α. Порівняти довжини похилих ?
α. Порівняти довжини похилих ?
Розв’язування
Оскільки перпендикуляр і три похилі проведені з 1 точки до 1 площини, то з трьох похилих більше та, _______________ якої _______________.
МО=4 - катет, прилеглий до кута між перпендикуляром ______ і похилими _____,______
і______, тому довжини похилих обчислюється за формулами:
АМ=![]() ( З ∆AOM, < AOM=______°), АМ=
( З ∆AOM, < AOM=______°), АМ=![]() ----------------
----------------
ВМ=![]() =___________( З ∆ВOM, < ВOM=______°),
=___________( З ∆ВOM, < ВOM=______°),
СМ=![]() =___________( З ∆СOM, < СOM=______°).
=___________( З ∆СOM, < СOM=______°).
Відповідь:________<________<________
Завдання 3.
Виконати графічний диктант, запропонований вчителем.
Записуєте в робочих зошитах відповіді на запитання диктанту, користуючись символами «так»-∩, «ні»- ─, а потім здійснюєте самоперевірку за ключем – відповіддю, запропонованим вчителем.
Урок №10
« Математика цікава тоді,
коли дає поживу нашій
винахідливості й
здатності до міркувань»
Д. Пойа
Фронтальне опрацювання матеріалу
Теорема про три перпендикуляри
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези блоку № 3.
- Усно дайте відповіді на питання:
- Які прямі називаються перпендикулярними?
- Які пряма і площина називаються перпендикулярними?
- Сформулюйте ознаку перпендикулярності прямої і площини.
- Дайте визначення перпендикуляра і похилої.
- Сформулюйте властивості перпендикуляра і похилої.
- Сформулюйте теорему про три перпендикуляра.
- Сформулюйте теорему, обернену до теореми про три перпендикуляри.
 Завдання 2.
Завдання 2.
Усно виконати вправи:
- До площини квадрата ABCD проведено перпендикуляр SA (див. рисунок). Вкажіть пряму, яка перпендикулярна до прямої SD.
|
А |
Б |
В |
Г |
Д |
|
AC |
DB |
BC |
CD |
SA |
-
Намалюйте куб
 , О – центр грані АВСD, вкажіть пряму, яка перпендикулярна до прямої
, О – центр грані АВСD, вкажіть пряму, яка перпендикулярна до прямої 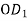 .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
Намалюйте куб
 . Вкажіть проекцію похилої
. Вкажіть проекцію похилої 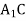 на площину
на площину 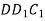 .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Виконайте письмово вправи:
-
Намалюйте куб
 , точка О – центр грані АВСD. Встановіть відповідність між заданими прямими (1 – 4) та прямими (А – Д), які перпендикулярні до заданих.
, точка О – центр грані АВСD. Встановіть відповідність між заданими прямими (1 – 4) та прямими (А – Д), які перпендикулярні до заданих.
1 пряма ![]() А пряма
А пряма ![]()
2 пряма ![]() Б пряма
Б пряма ![]()
3 пряма ![]() В пряма
В пряма ![]()
4 пряма ![]() Г пряма
Г пряма ![]()
Д пряма ![]()
-
До площини квадрата АВСD проведено перпендикуляр SB; SВ = 8 см, АС =
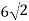 см. Знайдіть відстань від точки S до прямої СD.
см. Знайдіть відстань від точки S до прямої СD.
-
Дано правильний трикутник АВС зі стороною
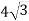 см. Точка S рівновіддалена від усіх сторін цього трикутника. Знайдіть відстань від точки S до сторони АВ, якщо відстань від точки S до площини АВС дорівнює
см. Точка S рівновіддалена від усіх сторін цього трикутника. Знайдіть відстань від точки S до сторони АВ, якщо відстань від точки S до площини АВС дорівнює 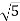 см.
см.
 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
-
До площини квадрата АВСD проведено перпендикуляр SB; SВ = 12 см, АС =
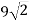 см. Знайдіть відстань від точки S до прямої AD.
см. Знайдіть відстань від точки S до прямої AD.
-
Дано правильний трикутник АВС зі стороною
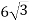 см. Точка S рівновіддалена від усіх сторін цього трикутника. Знайдіть відстань від точки S до площини АВС, якщо відстань від точки S до сторони ВС дорівнює
см. Точка S рівновіддалена від усіх сторін цього трикутника. Знайдіть відстань від точки S до площини АВС, якщо відстань від точки S до сторони ВС дорівнює 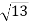 см.
см.
Урок №12
«Не роби ніколи того, чого не знаєш. Але вчись усьому,
що потрібно знати, і тоді будеш вести спокійне життя»
Піфагор
Внутрішньопредметне узагальнення матеріалу
Перпендикулярність прямих у просторі. Перпендикулярність прямої і площини
І. Узагальнення теоретичних знань
Завдання 1.
- Повторити блок № 3.
- Письмово дати відповідь на питання, запропоновані вчителем.
ІІ. Узагальнення практичних умінь та навичок
Завдання 2.
Письмово виконати вправи:
-
Точка О – центр квадрата АВСD,
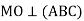 ,
, 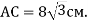 Знайдіть відстань від точки М до площини АВС, якщо МD = 8 см.
Знайдіть відстань від точки М до площини АВС, якщо МD = 8 см.
-
Точка О – центр квадрата АВСD,
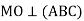 ,
, 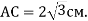 Знайдіть відстань від точки М до точки D, якщо відстань від точки М до площини АВС дорівнює 1 см.
Знайдіть відстань від точки М до точки D, якщо відстань від точки М до площини АВС дорівнює 1 см.
- Відстань від точки S до кожної з вершин квадрата АВСD дорівнює 5 см. Знайдіть відстань від точки S до площини квадрата, якщо його діагональ дорівнює 6 см.
- Відстань від точки S до кожної з вершин квадрата АВСD дорівнює 5 см. Знайдіть діагональ квадрата АВСD, якщо відстань від точки S до його площини дорівнює 3 см.
-
Точка S рівновіддалена від кожної сторони рівностороннього трикутника АВС, сторона якого дорівнює
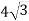 см. Знайдіть відстань від точки S до сторони АВ, якщо відстань від точки S до площини АВС дорівнює
см. Знайдіть відстань від точки S до сторони АВ, якщо відстань від точки S до площини АВС дорівнює 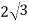 см.
см.
- Відстань від точки S до кожної з вершин правильного трикутника АВС дорівнює 5 см. Знайдіть відстань від точки S до площини трикутника АВС, якщо його медіана дорівнює 12 см.


про публікацію авторської розробки
Додати розробку