Посібник для уроків геометрії ІІ семестр 10 класу
Тема №4. Перпендикулярність площин
Урок №1

Перпендикулярність площин
«…наочне розуміння грає
першочергову роль у геометрії»
Д. Гільберт
Питання
- Двогранний кут. Перпендикулярність площин
- Відстані у просторі
- Кути у просторі
- Ортогональне проектування
Література
Істер О.С. Математика: (алгебра і початки аналізу та геометрія, рівень стандарту): Підручник для 10 класу закладів загальної середньої освіти. Київ: Генеза, 2018 рік, розділ Геометрія, §§8 – 10, стор. 298 – 322.
|
1. Двогранний кут. Перпендикулярність площин |
||
|
1.1 |
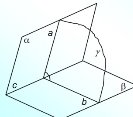
Двогранним кутом називають фігуру, яка утворена двома півплощинами зі спільною прямою, що їх обмежує |
|
|
1.2 |
Градусною мірою двогранного кута називають градусну міру його лінійного кута. |
|
|
1.3 |
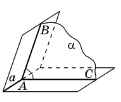
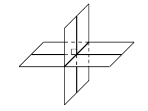
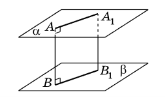
Дві площини, що перетинаються називаються перпендикулярними, якщо, перетинаючись, вони утворюють прямі двогранні кути.
|
|
|
1.4 |
Теорема (ознака перпендикулярності площин) Якщо площина проходить через пряму, перпендикулярну до другої площини, то ці площини перпендикулярні |
|
|
2. Відстані у просторі |
||
|
2.5 |
Відстанню від точки до прямої називається довжина перпендикуляра, проведеного з цієї точки до прямої |
АВ – відстань від точки А до прямої а |
|
2.6 |
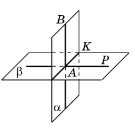
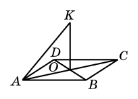
Відстанню від точки до площини є довжина перпендикуляра, проведеного з цієї точки до площини |
ОК – відстань від точки К до площини АВС |
|
2.7 |
Відстанню від прямої до паралельної їй площини називають довжину перпендикуляра, проведеного з будь – якої точки цієї прямої до площини |
АВ – відстань від прямої а до площини |
|
2.8 |
Відстанню між паралельними площинами називають довжину перпендикуляра, проведеного з будь – якої точки однієї площини до іншої |
АВ – відстань від площини α до площини β |
|
3. Кути у просторі |
||
|
3.9 |
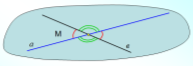
Кутом між прямими, які перетинаються називають менший із кутів, що утворились при перетині цих прямих.
|
|
|
3.10 |
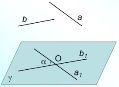
Кутом між мимобіжними прямими називається кут між прямими, що перетинаються і паралельні даним мимобіжним прямим |
|
|
3.11 |
Кутом між прямою і площиною називається кут між цією прямою і її проекцією на площину
|
|
|
3.12 |
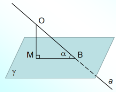
Кутом між площинами, які перетинаються, називається кут між прямими, проведеними в цих площинах перпендикулярно до лінії їх перетину |
|
|
3.13 |
Кут між паралельними площинами дорівнює 0° |
|
|
4. Ортогональне проектування |
||
|
4.14 |
Якщо напрям паралельного проектування перпендикулярний до площини проекції, то таке проектування називають ортогональним або прямокутним |
|
|
4.15 |
Площа ортогональної проекції многокутника на площину дорівнює добутку його площі на косинус кута між площиною многокутника і площиною проекції
|
|
Урок №2
«Серед рівних розумом, за однакових
умов, перемагає той, хто знає геометрію»
Блез Паскаль
Фронтальне опрацювання матеріалу
Двогранний кут. Перпендикулярність площин
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 1.4 блоку № 4.
- Усно дати відповідь на питання:
- Які площини називаються перпендикулярними?
- Сформулюйте ознаку перпендикулярності площин.
- Що називають двогранним кутом?
- Як обчислити градусну міру двогранного кута?
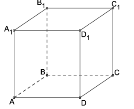
Завдання 2.
Усно виконати вправи:
-
Дано куб
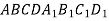 . Вкажіть площину, яка перпендикулярна до площини
. Вкажіть площину, яка перпендикулярна до площини 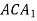 .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
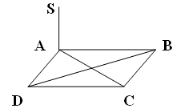
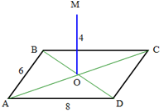
- До площини квадрата ABCD (точка О – центр квадрата) проведено перпендикуляр SA (див. малюнок). Вкажіть площину, яка перпендикулярна до площини МAD.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
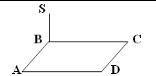
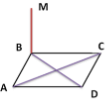
- До площини прямокутника ABCD проведено перпендикуляр SB (див. малюнок). Вкажіть спільний перпендикуляр прямих SB і AD.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
-
Площини квадратів
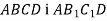 перпендикулярні,
перпендикулярні, 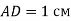 . Обчислити довжину відрізка
. Обчислити довжину відрізка  .
.
-
Площини рівносторонніх трикутників
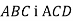 перпендикулярні,
перпендикулярні, 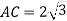 см. Обчислити довжину відрізка BD.
см. Обчислити довжину відрізка BD.
-
Площини прямокутних трикутників
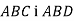 з прямими кутами С і D перпендикулярні. Обчислити довжину відрізка АВ, якщо
з прямими кутами С і D перпендикулярні. Обчислити довжину відрізка АВ, якщо 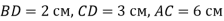 .
.
-
З точок А і В, які лежать у перпендикулярних площинах, проведено перпендикуляри АС і BD до прямої перетину даних площин. Обчислити довжину відрізка АВ, якщо
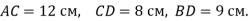
- Кінці відрізка лежать у двох перпендикулярних площинах. Проекції відрізка на площини дорівнюють 20 см і 16 см. Відстань між основами перпендикулярів, проведених з кінців відрізка до лінії перетину площин, дорівнює 12 см. Знайдіть довжину даного відрізка.
Уроки №3, 4
«Поводься так, ніби ти вже
щасливий, і ти дійсно станеш щасливішим»
Дейл Карнегі
Фронтальне опрацювання матеріалу
Відстані у просторі
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 2.8 блоку № 4.
- Усно дати відповідь на питання:
- Які площини називаються перпендикулярними?
- Як читається ознака перпендикулярності площин?
- Що називають двогранним кутом?
- Що називається відстанню від точки до прямої?
- Що називається відстанню від прямої до паралельної їй площини?
- Що називається відстанню між паралельними площинами?
- Що називають відстанню від точки до площини?
 Завдання 2.
Завдання 2.
Усно виконати вправи:
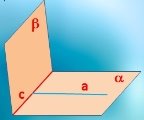
-
Пряма
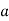 лежить у площині
лежить у площині 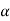 і
і 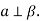 Чи випливає з цього, що
Чи випливає з цього, що 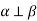 ?
?
-
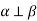 . Пряма а лежить у площині
. Пряма а лежить у площині 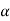 і
і 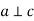 . Чи можна стверджувати, що
. Чи можна стверджувати, що 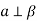 ?
?
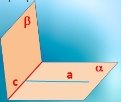
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
-
Відрізок довжиною
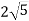 см опирається кінцями на дві перпендикулярні площини. Проекції відрізка на ці площини дорівнюють
см опирається кінцями на дві перпендикулярні площини. Проекції відрізка на ці площини дорівнюють 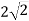 см і 4 см. Знайдіть відстані від кінців відрізка до даних площин.
см і 4 см. Знайдіть відстані від кінців відрізка до даних площин.
-
Відрізок довжиною
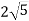 см опирається кінцями на дві перпендикулярні площини. Відстані від кінців відрізка до площини дорівнюють 2 см і
см опирається кінцями на дві перпендикулярні площини. Відстані від кінців відрізка до площини дорівнюють 2 см і 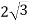 см. Знайдіть проекції відрізка на кожну площину.
см. Знайдіть проекції відрізка на кожну площину.
-
Через вершину А ромба АВСD проведено перпендикуляр SA до площини ромба. Знайдіть відстань між прямими SA і DC, якщо
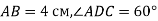 .
.
-
Через вершину А ромба АВСD проведено перпендикуляр SA до площини ромба. Знайдіть відстань між прямими SA і ВC, якщо
 .
.
- Через вершину В рівнобедреного трикутника АВС проведено пряму а, перпендикулярну до його площини. Знайдіть відстань між прямими а і АС, якщо АВ = АС = 10 см, ВС = 12 см.
- Площини прямокутників АВСD і АВЕF перпендикулярні. Знайдіть відстань між прямими DE і АВ, якщо AF = 8 см, ВС = 15 см.
Урок №5
Вивчай все не заради марнославства,
а заради практичної користі.
Г. Сковорода
Фронтальне опрацювання матеріалу – практична робота
Відстані у просторі
Оціночна картка роботи на уроці учня
|
Знання блоку |
Дешифровка (0-3,2) |
Робота в парах (0-7) |
Пропуски в задачах (0-9) |
Фронтальне опитування (0-7) |
Самостійна робота (0-6) |
Всього (0-40) |
|
Бліц- опитування (0-2,8) |
||||||
|
|
|
|
|
|
|
|
Знання блоку
Теоретичний блок. Бліц опитування «Так – ні» (за кожну правильну відповідь по 0,2 бали)
Чи правильне твердження?
1. Через будь-яку пряму можна провести площину, перпендикулярну до заданої.
2. Якщо пряма паралельна одній з двох перпендикулярних площин, то вона перпендикулярна й до другої.
3. Якщо дві площини перпендикулярні до третьої, то вони можуть бути паралельними.
4. Якщо дві площини перпендикулярні до третьої, то вони перпендикулярні між собою.
5. Якщо пряма перетинає одну з двох перпендикулярних площин, то вона перетинає й другу
6. Якщо площина перпендикулярна до заданої площини, то вона перпендикулярна і до будь-якої прямої, паралельної цій площині.
7. Площини вертикальних діагональних перерізів куба є взаємно перпендикулярними.
8. Якщо пряма паралельна одній з двох перпендикулярних площин, то вона
паралельна і другій.
9. Через точку, взяту поза площиною, можна провести площину, перпендикулярну до цієї площини, і причому тільки одну.
10. Якщо пряма паралельна одній з двох перпендикулярних площин, то вона лежить в другій площині.
11. Якщо дві площини перпендикулярні до третьої, то вони не можуть перетинатися.
12. Якщо площина і пряма перпендикулярні до однієї й тієї самої площини, то вони паралельні між собою.
13. Якщо дві площини перпендикулярні до третьої площини, то пряма їх перетину також перпендикулярна до тієї самої площини.
14. Через перпендикуляр до заданої площини можна провести єдину площину, перпендикулярну цій площині.
Мотивація навчальної діяльності учнів
Тема уроку з’ясовується учнями самостійно за допомогою дешифровки. (Запишіть перші літери слів, запропонованих означеннями)
|
|
Буква |
|
Буква |
|
|
Частина прямої, що лежить між двома точками |
|
|
|
Відрізок, що сполучає дану точку з точкою площини і лежить на прямій, перпендикулярній до площини. |
|
Чорна, червона, кабачкова |
|
|
Результат віднімання |
|
|
Хорда, що проходить через центр кола. |
|
|
Паралельні сторони трапеції |
|
|
Розділ геометрії, який вивчаємо |
|
|
Відношення протилежного катета до гіпотенузи у прямокутному трикутнику |
|
|
Твердження, що потребує доведення |
|
|
Рівнобедрений . . . |
|
|
Твердження, що не потребує доведення |
|
|
.… координат |
|
|
5-5= |
|
|
Чотирикутник, всі сторони якого рівні. |
|
|
Сухофрукт із винограду |
|
|
М’ясо птиці, не курятина |
Розв’язування вправ
- Робота в парах (за кожну правильну відповідь по 0,5 бали)
|
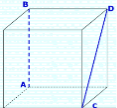
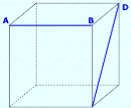
1. На зображенні куба вкажіть спільний перпендикуляр до прямих АВ і СD |
|||||
|
|
|
|
|
||
|
Продовжити речення:
|
|||||
|
1) Відстанню від точки М до |
|||||
|
прямої АВ буде довжина відрізка … |
прямої АD буде довжина відрізка … |
прямої АС буде довжина відрізка … |
|||
|
2) Відстанню між прямими ВМ і АD буде довжина відрізка … |
|||||
|
3) Відстанню між прямими AD і DC буде довжина відрізку … |
|||||
|
Продовжити речення: |
|||||
|
1) Відстань між прямими МО і АВ дорівнює … |
|||||
|
2) Відстань між прямими МО і ВС дорівнює … |
|||||
|
3) Відстань від точки А до прямої МО дорівнює … |
|||||
|
4) Відстань від точки М до прямої АВ дорівнює … |
|||||
|
5) Відстань від точки М до точки В дорівнює … |
|||||
- Виконаємо разом: за готовими рисунками заповнимо пропуски в розв’язуванні
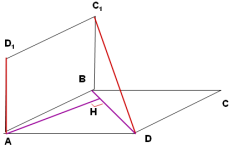 Задача 1. ( за кожен заповнений пропуск по 0,5 бали)
Задача 1. ( за кожен заповнений пропуск по 0,5 бали)
Рівні прямокутники ABCD і ABC1D1 лежать у перпендикулярних площинах. Знайдіть відстань між мимобіжними прямими AD1 і С1D, якщо АВ=15 см, ВС=20 см
Розв’язання
Оскільки D1A і C1В – … до прямої перетину двох перпендикулярних площин, то D1A … (АВС), С1В … (АВС).
Побудуємо ортогональні проекції прямих AD1 і С1D на площину АВС.
Проекціями є відповідно … та … . Шукана відстань дорівнює висоті АН ΔABD (A=900).
За теоремою Піфагора ВD = … см, то ![]()
Відповідь: … см
Задача 2. ( за кожен заповнений пропуск по 1 балу)
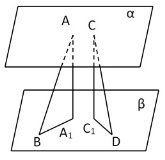
Два відрізка упираються своїми кінцями в дві паралельні площини різниця цих відрізків дорівнює 17 см а їх проекції на одну із площин дорівнюють 9 см і 42см знайти відстань між площинами.
 Розв’язання
Розв’язання
Нехай α![]() β, АВ, CD - дані відрізки, АВ – СD = 17 cм, AA1
β, АВ, CD - дані відрізки, АВ – СD = 17 cм, AA1![]() BA1= 42 cм, C1D = 9 cм.
BA1= 42 cм, C1D = 9 cм.
Нехай CD = x cм, тоді АВ = … см.
Із ![]() АВА1: AA12 = AB2 - A1B2 = …
АВА1: AA12 = AB2 - A1B2 = …
Із ![]() CC1D: CC12 = CD2 - C1D2 = …
CC1D: CC12 = CD2 - C1D2 = …
Враховуючи, що AA1 = СС1, маємо …
Отже CD = … cм, CC1= … cм.
- Самостiйна робота із взаємоперевіркою за зразком на дошці (з обґрунтуванням по 3 бали)
|
№ |
Варiант 1 |
Варiант 2 |
|
1 |
Пряма CD перпендикулярна площинi гострокутного трикутника ABC, CK — його висота. Доведiть, що прямi DK i AB взаємно перпендикулярнi. Знайдiть вiдстань вiд точки A до площини DKC, якщо DA = |
Діагоналі чотирикутника ABCD перетинаються в точці O. З точки O проведено перпендикуляр OM до прямої AB i перпендикуляр OK до площини чотирикутника. Доведiть, що кут між прямими MK i AB прямий. Знайдiть вiдстань вiд точки B до площини OKM, якщо KM = |
|
2 |
Площини α i β перпендикулярнi. Рівносторонній трикутник ABC лежить у площинi α так, що сторона AB належить прямій перетину площин. Пряма b лежить у площинi β, паралельна прямій перетину площин i віддалена вiд неї на 4 см. Обчисліть вiдстань вiд точки C до прямої b, якщо AB = |
Площини α i β перпендикулярнi. Рівнобедрений трикутник ABC лежить у площинi α так, що його основа AB належить прямій перетину площин. Пряма b лежить у площинi β, паралельна прямій перетину площин i віддалена вiд неї на 5 см. Обчисліть вiдстань вiд точки C до прямої b, якщо AB = 32 см, AC = 20 см. |
 4. Фронтальне опитування ( за кожну повну відповідь по 1балу)
4. Фронтальне опитування ( за кожну повну відповідь по 1балу)
1. Дайте визначення ключового слова у всіх означеннях відстаней у просторі.
2. Сформулюйте означення вiдстанi та проілюструйте кожне з них на відповідних моделях або предметах навколишнього середовища:
а) від точки до прямої;
б) від точки до площини;
в) від прямої до площини;
г) між площинами;
д) між паралельними прямими;
е) між мимобіжними прямими.
Оцінювання навчальних досягнень учнів
Таблиця переводу отриманих балів
|
Набрані бали |
35-33 |
32-30 |
29-26 |
25-22 |
21-18 |
17-13 |
12-8 |
7-4 |
|
Оцінка |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |

 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
-
За зображенням куба
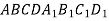 встановіть відповідність між заданими площинами (1 – 4) та перпендикулярними до них площинами (А – Д).
встановіть відповідність між заданими площинами (1 – 4) та перпендикулярними до них площинами (А – Д).
1 ![]() A
A ![]()
2 ![]() Б
Б ![]()
3 ![]() В
В ![]()
4 ![]() Г
Г ![]()
Д ![]()
-
Відрізок довжиною
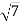 см опирається кінцями на дві перпендикулярні площини. Відстані від кінців відрізка до площини дорівнюють 1 см і
см опирається кінцями на дві перпендикулярні площини. Відстані від кінців відрізка до площини дорівнюють 1 см і  см. Знайдіть проекції відрізка на кожну площину.
см. Знайдіть проекції відрізка на кожну площину.
-
Через вершину А ромба АВСD проведено перпендикуляр SA до площини ромба. Знайдіть відстань між прямими SA і ВC, якщо
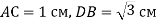 .
.
Уроки №7, 8
90% наших турбот стосується того,
що ніколи не станеться
Маргарет Тетчер
Фронтальне опрацювання матеріалу
Кути у просторі
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
Повторіть тези 3.9 – 3.13 блоку № 4 і дайте відповіді на питання:
- Які існують кути у просторі?
- Якщо дві прямі перетинаються у просторі, то вони утворюють…
- Кут між даними прямими – це…
- Кут між мимобіжними прямими – це кут…
- Дві прямі називаються перпендикулярними, якщо…
- Перпендикуляром, опущеним з даної точки на площину, називається відрізок…
- Відрізок, який сполучає дану точку з точкою площини і не є перпендикуляром, називається…
- Рівні похилі мають… Наведіть іншу властивість.
- Проекція – це…
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
2.1. Знайдіть довжину проекції похилої та відстань від точки А до площини α, якщо похила дорівнює 10см і утворює із площиною кут ![]() .
.
2.2. Рівносторонній трикутник АВЕ і квадрат АВСD мають спільну сторону АВ довжиною 4 см. Знайдіть кут між площинами, якщо ![]()
2.3. Квадрат і прямокутник, площі яких відповідно дорівнюють ![]() і
і ![]() , мають спільну сторону, а кут між їх площинами дорівнює
, мають спільну сторону, а кут між їх площинами дорівнює ![]() . Знайдіть відстань між паралельними сторонами трикутника і квадрата.
. Знайдіть відстань між паралельними сторонами трикутника і квадрата.
Завдання 3.
- З точки P до площини β проведено похилу, яка утворює з площиною кут 30°. Знайдіть довжину похилої та відстань від точки P до площини β, якщо проекція похилої на площину дорівнює 6 см.
-
З точки M до площини α проведені похилі MB і MC, які утворюють кути по 30° з площиною. Знайдіть відстань від точки M до площини α, якщо
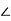 BMC=90°, а довжина відрізка BC дорівнює 8 см.
BMC=90°, а довжина відрізка BC дорівнює 8 см.
-
Площини α і β перетинаються по прямій а. У площині α вибрано точку K і з неї проведено перпендикуляр KM до площини β. Відстань від точки K до площини β дорівнює
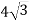 см, а відстань від точки M до прямої а дорівнює 4см. Знайдіть кут між площинами α і β.
см, а відстань від точки M до прямої а дорівнює 4см. Знайдіть кут між площинами α і β.
- Кут між площинами рівнобедрених трикутників ABC і ABD дорівнює 60° (AB – спільна основа трикутників). Знайдіть відстань між точками C і D, якщо AC=10см, AD=17см, AB=16см.
Урок №9
«Чи не дивина, що один у багатстві
бідний, а інший у бідності багатий?»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Кути у просторі. Площа ортогональної проекції многокутника
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези блоку № 4.
- Усно дайте відповіді на питання:
- Що вважають кутом між прямими, які перетинаються?
- Що називають кутом між прямою і площиною?
- Що є кутом між мимобіжними прямими?
- Що називають кутом між площинами, які перетинаються?
- Чому дорівнює кут між паралельними площинами?
- Що називають ортогональним проектуванням?
-
 Чому дорівнює площа ортогональної проекції многокутника на площину?
Чому дорівнює площа ортогональної проекції многокутника на площину?
Завдання 2.
Усно виконати вправи:
-
Дано куб
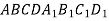 . Користуючись малюнком, вкажіть градусну міру кута між прямою
. Користуючись малюнком, вкажіть градусну міру кута між прямою  та прямою
та прямою 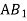 .
.
|
А |
Б |
В |
Г |
Д |
|
0° |
30° |
45° |
60° |
90° |
-
Знайдіть кут між похилою і площиною, якщо довжина похилої дорівнює 8 см, а проекція похилої на площину дорівнює
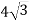 см.
см.
|
А |
Б |
В |
Г |
Д |
|
0° |
30° |
45° |
60° |
90° |
-
Знайдіть площу ортогональної проекції многокутника на задану площину, якщо площа многокутника дорівнює
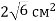 , а кут між даною площиною і площиною многокутника дорівнює 45°.
, а кут між даною площиною і площиною многокутника дорівнює 45°.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Письмово виконати вправи:
-
Знайти площу ортогональної проекції многокутника, площа якого дорівнює
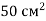 , а кут між площиною многокутника і його проекцією — 60°.
, а кут між площиною многокутника і його проекцією — 60°.
- Знайти площу многокутника, якщо площа ортогональної проекції цього многокутника дорівнює 50 см2, а кут між площиною многокутника і його проекцією дорівнює 45°.
-
Площа многокутника дорівнює
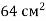 , а площа ортогональної проекції —
, а площа ортогональної проекції — 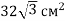 . Знайдіть кут між площинами многокутника і його проекцією.
. Знайдіть кут між площинами многокутника і його проекцією.
-
Рівнобедрені трикутники МРК і МЕК мають спільну основу МК. Знайдіть кут між площинами цих трикутників, якщо МК = 24см, РК =
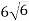 см, КЕ = 13см, РЕ =
см, КЕ = 13см, РЕ =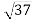 см.
см.
-
Кут між площинами трикутників АВС і АКС дорівнює
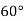 , АС = 24см, ВС= ВА = 20 см, КС = КА = 15см. Знайдіть довжину відрізка ВК.
, АС = 24см, ВС= ВА = 20 см, КС = КА = 15см. Знайдіть довжину відрізка ВК.
 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
- Знайти площу многокутника, якщо площа ортогональної проекції цього многокутника дорівнює 34 см2, а кут між площиною многокутника і його проекцією дорівнює 60°.
-
Кут між площинами трикутників АВС і АКС дорівнює
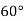 , АС = 20 см, ВС = ВА = 26 см, КС = КА =
, АС = 20 см, ВС = ВА = 26 см, КС = КА =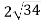 см. Знайдіть довжину відрізка ВК.
см. Знайдіть довжину відрізка ВК.
Урок № 11
«Не роби ніколи того, чого не знаєш. Але вчись усьому,
що потрібно знати, і тоді будеш вести спокійне життя»
Піфагор
Внутрішньопредметне узагальнення матеріалу
Перпендикулярність площин
І. Узагальнення теоретичних знань
Завдання 1.
- Повторити блок № 4.
- Письмово дати відповідь на питання, запропоновані вчителем.
ІІ. Узагальнення практичних умінь та навичок
Завдання 2.
![]()
 Усно виконати вправи: S
Усно виконати вправи: S
-

 До площини паралелограма ABCD проведено А В перпендикуляр AS і
До площини паралелограма ABCD проведено А В перпендикуляр AS і 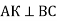 . Яка з указаних нижче площин перпендикулярна до площини К АВС? D С
. Яка з указаних нижче площин перпендикулярна до площини К АВС? D С
|
А |
Б |
В |
Г |
Д |
|
DSC |
SBK |
SBD |
SAB |
SDK |
-
З однієї точки до площини проведено перпендикуляр і похилу. Знайдіть кут між похилою і площиною, якщо довжина похилої дорівнює 6 см, а довжина перпендикуляра
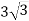 см.
см.
|
А |
Б |
В |
Г |
Д |
|
0° |
30° |
60° |
45° |
90° |
-
Зобразіть трикутну піраміду SABC, проведіть у ній
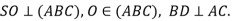 Вкажіть кут між площиною АВС і площиною SAC.
Вкажіть кут між площиною АВС і площиною SAC.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
∠SAB |
Завдання 3.
Письмово виконати вправи:
- Кут між площинами α і β дорівнює 60°. Точка А належить площині α. Знайдіть відстань від точки А до площини β, якщо відстань від точки А до лінії перетину площин дорівнює 12 см.
-
Знайдіть площу многокутника, якщо площа ортогональної проекції цього многокутника на площину α дорівнює 12
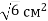 , а кут між площиною α і площиною многокутника дорівнює 60°.
, а кут між площиною α і площиною многокутника дорівнює 60°.
- Із однієї точки до площини проведено рівні похилі, які утворюють з перпендикуляром кути по 45°. Знайдіть кут між похилими, якщо кут між проекціями цих похилих на площину дорівнює 60°.
Тема №5. Координати і вектори у просторі
Урок №1

Координати та вектори у просторі
«Тим, хто не знає математики, важко
збагнути справжню, глибоку красу природи»
Річард Фейнман, американський фізик
Питання
- Прямокутна система координат у просторі.
- Вектори у просторі.
Література
Істер О.С. Математика: (алгебра і початки аналізу та геометрія, рівень стандарту): Підручник для 10 класу закладів загальної середньої освіти. Київ: Генеза, 2018 рік, розділ Геометрія, §§11 – 14, стор. 324 – 355.
|
1. Прямокутна система координат у просторі |
||||
|
1.1 |
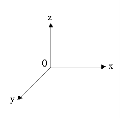
Коли кожній точці простору поставлена у відповідність трійка чисел, і навпаки, довільній трійці чисел відповідає єдина точка простору, – кажуть, що задано просторову систему координат. |
Ох – вісь абсцис Оу – вісь ординат Оz – вісь аплікат
Площини Знаки координат залежать від октанта, в якому міститься точка |
||
|
1.2 |
Простір із заданою в ньому системою координат називають координатним простором. |
|||
|
1.3 |
Квадрат відстані між двома точками дорівнює сумі квадратів різниць їх відповідних координат. |
|
||
|
1.4 |
Координати середини відрізка дорівнюють півсумі відповідних координат його кінців. |
|
||
|
2. Вектори у просторі |
||||
|
2.5 |
Відрізок, у якого вказаний напрям, називають вектором. |
|
||
|
2.6 |
Довжина напрямленого відрізка називається довжиною (модулем) вектора |
|||
|
2.7 |
Види векторів у стереометрії:
1) колінеарні – належать паралельним прямим (або одній прямій); 3) компланарні – паралельні одній площині або лежать в одній площині, але не колінеарні; 4) одиничні – модулі дорівнюють 1; 5) нульові – довжина дорівнює 0, напряму немає; 6) координатні вектори (орти) – одиничні вектори, напрям яких збігається з напрямком осей координат. |
|||
|
2.8 |
Вектори називаються рівними, якщо вони співнапрямлені та їх модулі рівні між собою. |
|||
|
2.9 |
Координати вектора дорівнюють різниці координат кінця і координат початку. |
|
||
|
2.10 |
Рівні вектори мають рівні координати, і навпаки, якщо у векторів рівні координати, то вектори рівні. |
Якщо
|
||
|
2.11 |
Модуль вектора, заданого координатами, дорівнює квадратному кореню із суми квадратів його координат. |
|
||
|
2.12 |
Кожна координата суми (різниці) двох векторів дорівнює сумі (різниці відповідних координат цих векторів. |
|
||
|
2.13 |
Добутком вектора |
|
||
|
2.14 |
Відповідні координати колінеарних векторів пропорційні. |
Якщо |
||
|
2.15 |
Скалярним добутком векторів |
|
||
|
2.16 |
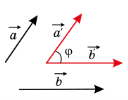
Кут між двома ненульовими векторами |
|
||
|
2.17 |
Властивості скалярного добутку векторів:
|
|||
Урок №2
«… нащадки будуть вдячні мені не тільки за те, що я сказав, але і за те,
що я не сказав і тим самим дав їм можливість і задоволення додуматися до цього самостійно»
Рене Декарт
Фронтальне опрацювання матеріалу
Прямокутна система координат у просторі. Координати точки
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 1.4 блоку № 5.
- Дайте відповідь на питання:
- Хто такий Рене Декарт?
- Скількома координатами може бути задана точка на прямій?
- Скількома координатами задана точка на координатній площині?
- Скількома координатами задана точка у просторі?
- Що називають координатами?
- Коли кажуть, що задано просторову систему координат?
- Як називаються осі координат у просторі?
Завдання 2.
Складіть алгоритм побудови точки у просторі на прикладі точки А(2; 3; 5).
Завдання 3.
- Які координати мають точки, якщо вони лежать на одній із осей координат у просторі?
- Які координати має точка, якщо вона лежить в одній із координатних площин?
Завдання 4.
Розв’яжіть усні вправи, запропоновані вчителем.
ІІ. Відпрацювання умінь і навичок розв’язування задачі вправ
Завдання 5.
Письмово виконати вправи:
-
Побудуйте точки
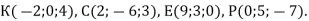
- Накреслити прямокутну тривимірну систему координат і позначити в ній точки:
![]() .
.
Урок №3
«Своє серце зверни до навчання,
а свої уші – до розумних речей.»
Книга приповістей Соломонових 23:12
Фронтальне опрацювання матеріалу
Відстань між точками. Координати середини відрізка
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 1.4 блоку № 5.
- Усно дати відповідь на питання:
- Що називають координатами точки?
- Що таке система координат?
- Коли кажуть, що задано просторову систему координат?
- Що називають координатним простором?
- Як знайти відстань між точками у координатному просторі?
- Як обчислити координати середини відрізка?
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
Письмово виконати вправи:
-
Знайдіть координати точки D паралелограма ABCD, якщо
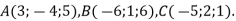
-
Точки
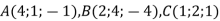 – середини сторін трикутника. Знайдіть координати вершин цього трикутника.
– середини сторін трикутника. Знайдіть координати вершин цього трикутника.
-
У трикутнику АВС відомо, що
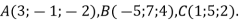 Знайдіть довжину середньої лінії MN трикутника АВС, де M і N – середини сторін АС і ВС відповідно.
Знайдіть довжину середньої лінії MN трикутника АВС, де M і N – середини сторін АС і ВС відповідно.
-
Знайдіть координати точок А і В та довжину відрізка АВ, якщо точка А належить осі z, точка В лежить у площині xy і точка
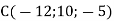 – середина відрізка АВ.
– середина відрізка АВ.
-
Доведіть, що точки
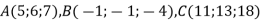 лежать на одній прямій. Яка з них лежить між двома іншими?
лежать на одній прямій. Яка з них лежить між двома іншими?
 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
-
Обчислити відстань між точками
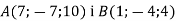 .
.
-
Обчислити координати середини відрізка АВ, якщо
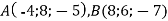 .
.
-
На рисунку зображено прямокутну систему координат у просторі, на осях якої позначено точки
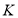 ,
, 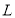 ,
, 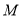 ,
, 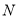 . Установіть відповідність між точками
. Установіть відповідність між точками 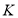 ,
, 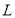 ,
, 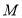 ,
,  (1 – 4) та їхніми можливими координатами (А – Д).
(1 – 4) та їхніми можливими координатами (А – Д).
-
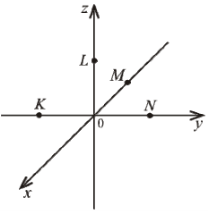
|
Точка |
Координати точки |
||
|
1 |
|
А |
|
|
2 |
|
Б |
|
|
3 |
|
В |
|
|
4 |
|
Г |
|
|
|
Д |
|
|
-
Точка
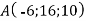 – один кінець відрізка, а точка
– один кінець відрізка, а точка 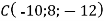 – його середина. Знайти другий кінець відрізка
– його середина. Знайти другий кінець відрізка 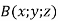 .
.
-
Довести, що чотирикутник
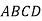 – ромб, якщо
– ромб, якщо 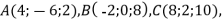
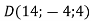 .
.
Уроки №5 – 7
«…з усіх втрат втрата часу найтяжча...»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Операції над векторами та їх властивості
І. Засвоєння термінології до теми
Завдання 1.
- Повторити тези 2.5 – 2.17 блоку № 5.
- Усно дати відповідь на питання:
- Що називають вектором?
- Що називають модулем вектора?
- Як знайти координати вектора?
- Чому дорівнює модуль вектора?
- Сформулювати властивість координат рівних векторів.
- Яку властивість мають координати колінеарних векторів?
- Чому дорівнюють координати суми, різниці векторів?
- Чому дорівнюють координати добутку вектора на число?
- Що називається скалярним добутком векторів?
- Сформулювати властивості скалярного добутку векторів.
- Сформулювати умову перпендикулярності векторів.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
Письмово виконати вправи:
-
Дано вектори
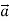 (4; – 5; 6) і
(4; – 5; 6) і 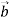 (– 1;2;5). Знайдіть: 1) координати векторів
(– 1;2;5). Знайдіть: 1) координати векторів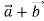 і
і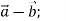
2) ![]() і
і ![]() .
.
-
Знайдіть координати точки С такої, що
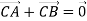 , де
, де 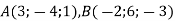 .
.
-
Знайдіть модуль вектора
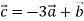 , де
, де 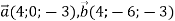 .
.
-
Чи колінеарні вектори
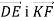 , якщо
, якщо 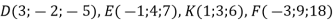 ?
?
-
Знайдіть значення y і z, при яких вектори
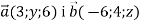 колінеарні.
колінеарні.
Завдання 3.
Письмово виконати вправи:
При якому найменшому значенні m довжина вектора ![]() буде більша за число 6?
буде більша за число 6?
Завдання 4.
Письмово виконати вправи:
-
Дано вектори
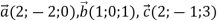 . Знайдіть: 1)
. Знайдіть: 1)  ; 2)
; 2) 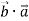 ; 3)
; 3) 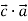 ; 4)
; 4) 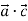 .
.
-
При якому значенні m скалярний добуток векторів
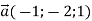 та
та 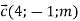 дорівнює: 1) 1; 2) 0
дорівнює: 1) 1; 2) 0
-
При якому від’ємному значенні m вектори
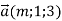 та
та 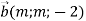 перпендикулярні?
перпендикулярні?
Завдання 5
Письмово виконати вправи:
-
Знайдіть скалярний добуток векторів
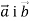 , якщо:
, якщо: 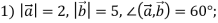
![]() .
.
-
Знайдіть скалярний добуток векторів
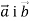 , якщо: 1)
, якщо: 1) 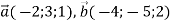 , 2)
, 2) 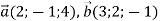 .
.
- Дано три точки А(0; 1; -1), В(1; -1; 2), С(3; 1; 0). Знайти косинус кута С трикутника АВС.
Завдання 6.
Гра «Математичне доміно»
(Учитель готує набір карток двох кольорів. На одних записується початок речення, на інших його закінчення; діти працюють в парах ).
|
Початок речення |
Закінчення речення |
|
Вектори називаються рівними … |
Якщо вони співнапрямлені і мають рівні довжини |
|
Два ненульових вектори називаються колінеарними….. |
Якщо вони паралельні одній прямій |
|
Щоб задати вектор… |
Достатньо вказати його початок і кінець. |
|
Два вектори називають протилежними векторами…. |
Якщо вони мають рівні модулі, але протилежні напрями. |
|
Співнапрямленими векторами називають колінеарні вектори… |
Якщо вони мають однаковий напрямок. |
|
Нуль-вектором називають вектор… |
Якщо його початок і кінець співпадають. |
|
Довжиною вектора називають… |
Відстань між його початком і кінцем. |
|
Довжина нуль-вектора…. |
Дорівнює нулю. |
|
Довжина і напрям вектора не залежать від… |
Розміщення його початку в системі координат |
|
Вектори рівні… |
Коли їх відповідні координати рівні. |
|
Вектори колінеарні… |
Коли їх відповідні координати пропорційні |
(Кожній парі учнів роздається доміно, яке необхідно скласти у відповідності: початок речення – кінець )
Завдання 7.
Користуючись рисунком, назвіть вектори, що є:
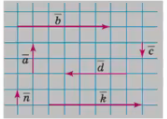 1) колінеарними;
1) колінеарними;
2) спів напрямленими;
3) протилежно напрямленими;
4) рівними;
5) протилежними?
Завдання 8.
Виконати самостійно завдання математичного диктанту
|
Математичний диктант Варіант 1 1.Запишіть коротко «вектор а».
2. Зобразити вектор 3.Запишіть позначення вектора з кінцем у точці Х та початком у точці У. 4.Зобразити два співнапрямлених, але не рівних вектора. 5.Що можна сказати про напрямок двох рівних векторів ? 6.Запишіть у вигляді рівності, чому дорівнює абсолютна величина нульового вектора.
7. Зобразити вектор
8. Запишіть за допомогою позначень «довжина вектора 9.Знайдіть довжину вектора, зображеного на рисунку:
3 см S 5 см
10. Чи вірно твердження: «Якщо вектори |
Математичний диктант Варіант 2 1.Запишіть коротко «вектор в».
2. Зобразити вектор 3.Запишіть позначення вектора з кінцем у точці Р та початком у точці А. 4.Запишіть у вигляді рівності, чому дорівнює абсолютна величина нульового вектора.
5. Зобразити вектор 6.Що можна сказати про напрямок двох рівних векторів ? 7.Зобразити два співнапрямлених, але не рівних вектора.
8. Запишіть за допомогою позначень «довжина вектора 9.Знайдіть довжину вектора, зображеного на малюнку:
К 2 см
6 см 10. Чи вірно твердження: «Якщо два вектори колінеарні, то вони співнапрямлені»?
|
Урок №8
«Невдача - це просто можливість
почати знову, але вже більш мудро»
Генрі Форд
Фронтальне опрацювання матеріалу
Вектори у просторі
І. Засвоєння термінології до теми
Завдання 1.
- Повторити тези 2.5 – 2.17 блоку № 5.
- Усно дати відповідь на питання:
- Що називають вектором?
- Що називають модулем вектора?
- Як знайти координати вектора?
- Чому дорівнює модуль вектора?
- Сформулювати властивість координат рівних векторів.
- Яку властивість мають координати колінеарних векторів?
- Чому дорівнюють координати суми, різниці векторів?
- Чому дорівнюють координати добутку вектора на число?
- Що називається скалярним добутком векторів?
- Сформулювати властивості скалярного добутку векторів.
- Сформулювати умову перпендикулярності векторів.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
Усно виконати вправи:
-
Дано точки
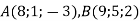 . Записати координати вектора
. Записати координати вектора 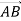 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Дано вектор
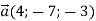 . Знайти координати вектора
. Знайти координати вектора  .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Дано вектори
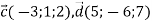 . Знайти координати вектора
. Знайти координати вектора 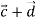 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
Завдання 3.
Письмово виконати вправи:
-
Дано вектори
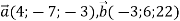 . Знайти модуль вектора
. Знайти модуль вектора 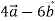 .
.
-
Точка
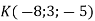 – кінець вектора
– кінець вектора 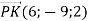 . Знайти координати початку цього вектора.
. Знайти координати початку цього вектора.
-
Дано вектори
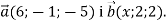 При якому значенні
При якому значенні 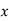 ці вектори перпендикулярні?
ці вектори перпендикулярні?
-
Дано три точки
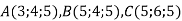 . Обчислити кут В трикутника АВС.
. Обчислити кут В трикутника АВС.
-
Дано вектор
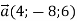 . Знайти колінеарний йому вектор з початком у точці
. Знайти колінеарний йому вектор з початком у точці 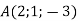 і кінцем у точці В на площині
і кінцем у точці В на площині  .
.
 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
-
Дано вектори
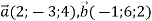 . Знайти модуль вектора
. Знайти модуль вектора 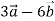 .
.
-
Точка
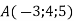 – кінець вектора
– кінець вектора  . Знайти координати початку цього вектора.
. Знайти координати початку цього вектора.
-
Дано вектори
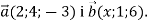 При якому значенні
При якому значенні 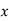 ці вектори перпендикулярні?
ці вектори перпендикулярні?
-
Дано три точки
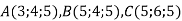 . Обчислити кут В трикутника АВС.
. Обчислити кут В трикутника АВС.
-
Дано вектор
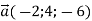 . Знайти колінеарний йому вектор з початком у точці
. Знайти колінеарний йому вектор з початком у точці 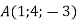 і кінцем у точці В на площині
і кінцем у точці В на площині 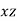 .
.
Урок №10
«Без бажання все важке, навіть найлегше»
Григорій Сковорода
Внутрішньопредметне узагальнення матеріалу
Координати та вектори у просторі
І. Засвоєння термінології до теми
Завдання 1.
- Повторити блок № 5.
- Письмово дати відповідь на питання, запропоновані вчителем.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
Усно виконати вправи:
-
Дано точки
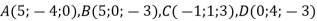 . Яка з цих точок лежить у площині
. Яка з цих точок лежить у площині  ?
?
|
А |
Б |
В |
Г |
|
D |
С |
В |
А |
-
Обчислити відстань від точки
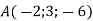 до початку координат.
до початку координат.
|
А |
Б |
В |
Г |
|
5 |
4 |
7 |
49 |
-
Дано вектори
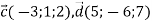 . Знайти координати вектора
. Знайти координати вектора 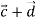 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
Завдання 3.
Письмово виконати вправи:
-
Дано точки
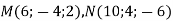 . Знайти координати середини відрізка
. Знайти координати середини відрізка 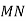 та його довжину.
та його довжину.
-
Дано точки
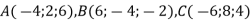 . Знайдіть: 1) координати векторів
. Знайдіть: 1) координати векторів 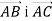 ; 2) модуль вектора
; 2) модуль вектора 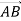 ; 3) координати вектора
; 3) координати вектора 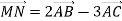 .
.
-
Чи існує паралельне перенесення, при якому образом точки
 є точка
є точка 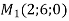 , а образом точки
, а образом точки 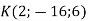 є точка
є точка 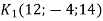 ?
?
-
Дано вектори
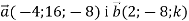 . При якому значенні
. При якому значенні 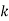 вектори
вектори 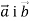 : 1) колінеарні; 2) перпендикулярні?
: 1) колінеарні; 2) перпендикулярні?
-
Довести, що чотирикутник
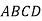 – ромб, якщо
– ромб, якщо  .
.
-
Точки
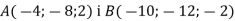 – вершини паралелограма ABCD, точка
– вершини паралелограма ABCD, точка 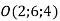 – точка перетину його діагоналей. Знайти координати вершин С і D паралелограма АВСD.
– точка перетину його діагоналей. Знайти координати вершин С і D паралелограма АВСD.
1
-
-
Чудова робота! Дякую! Теж використовую листи контролю теорії по темам.
-
Дякую! Велика допомога для створення дистанційного навчання з геометрії для 10 класів!


про публікацію авторської розробки
Додати розробку