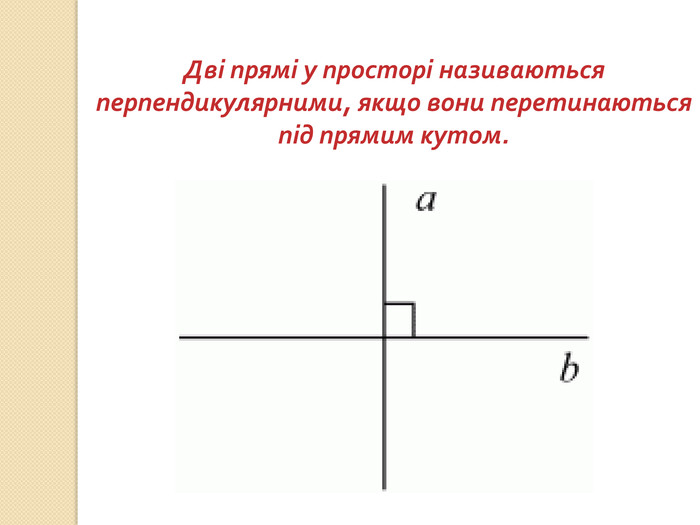
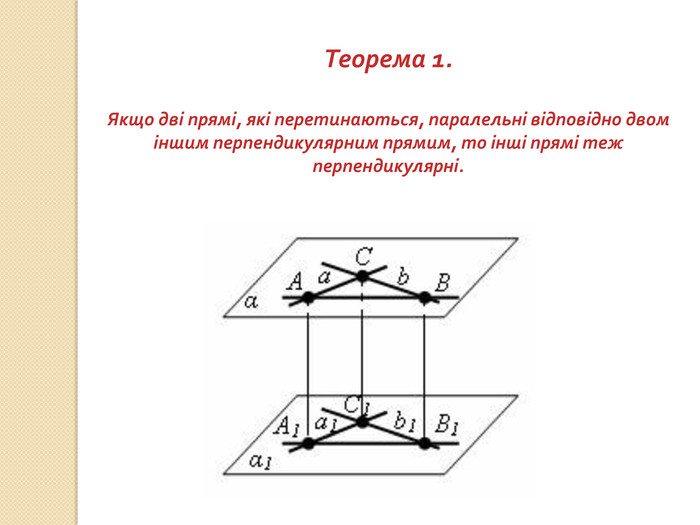
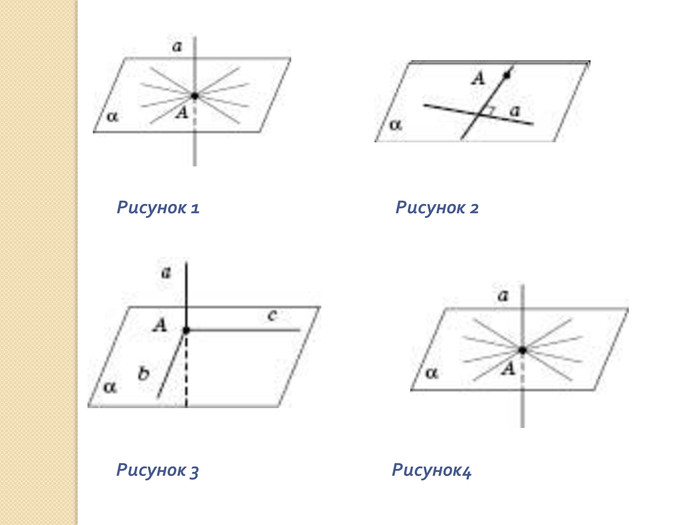
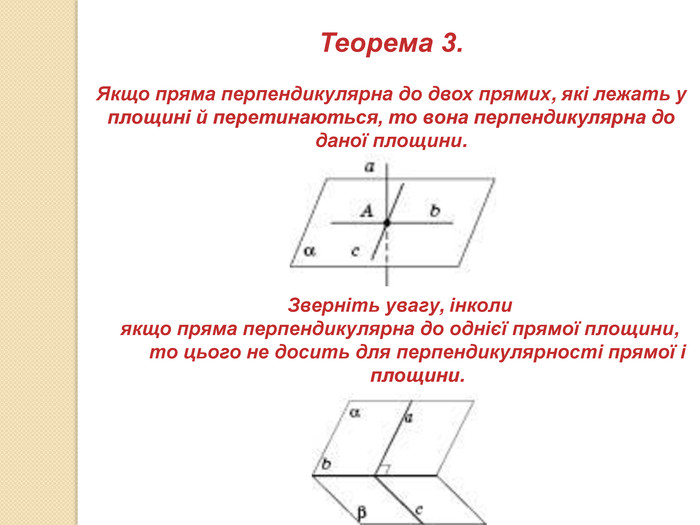
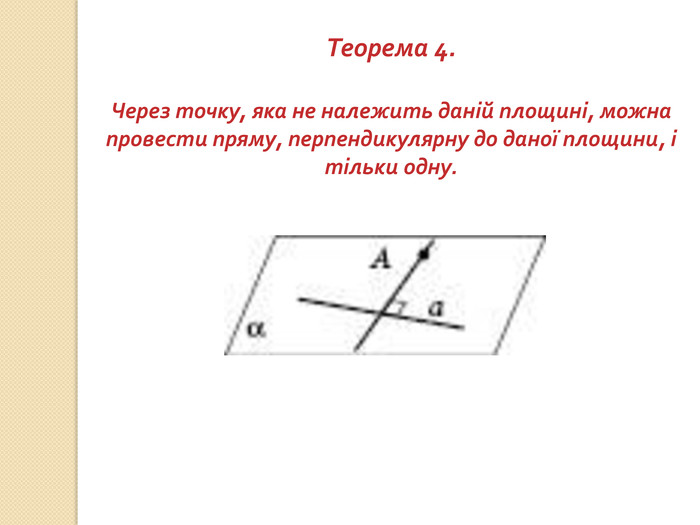
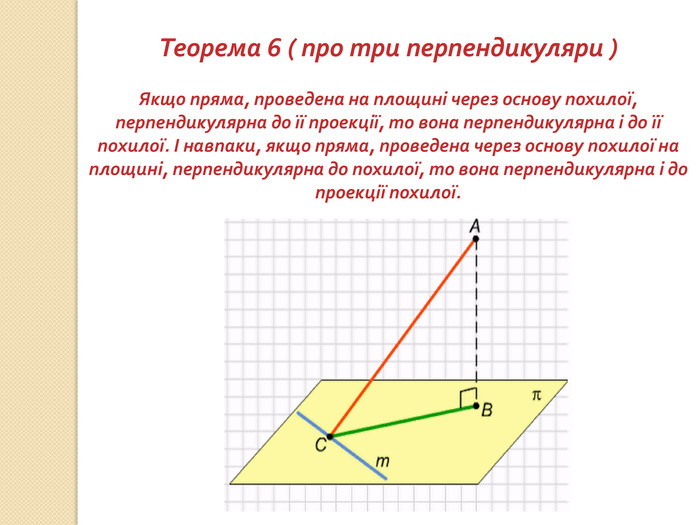
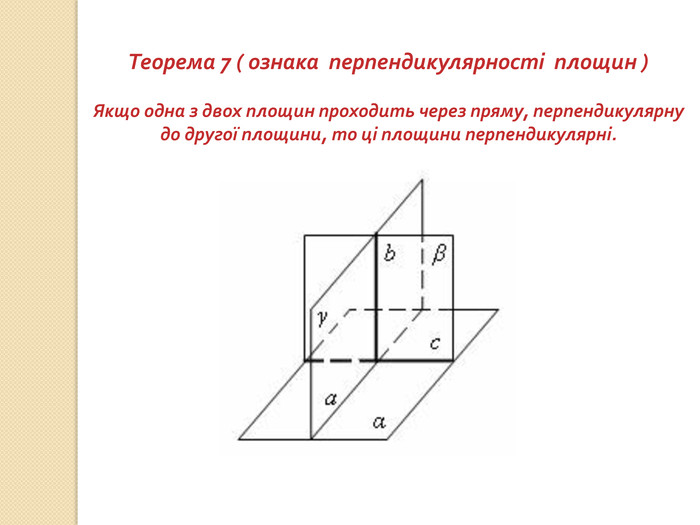
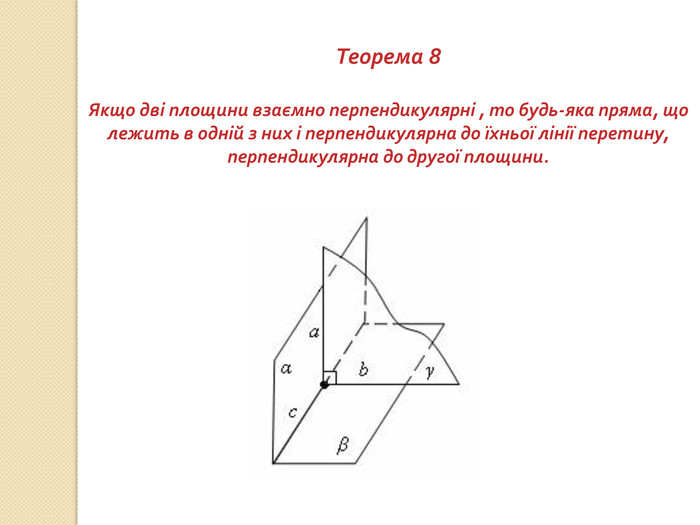
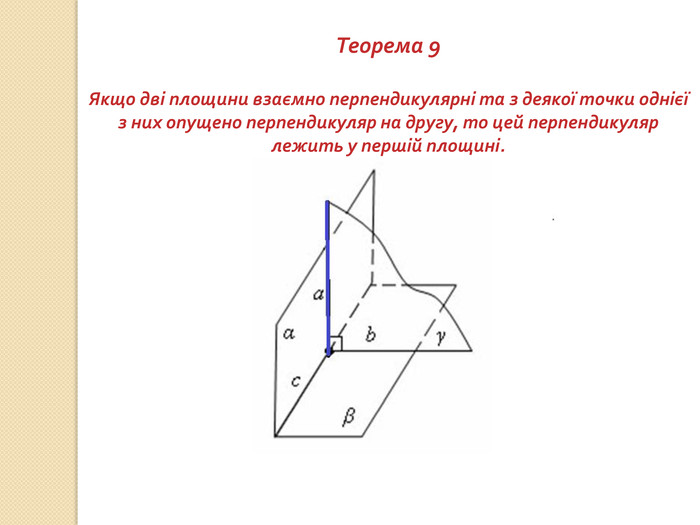
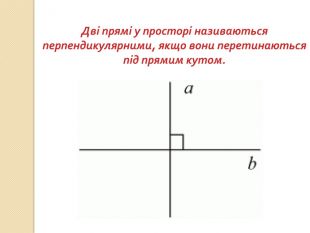
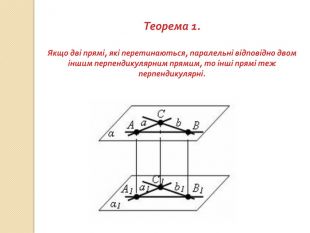
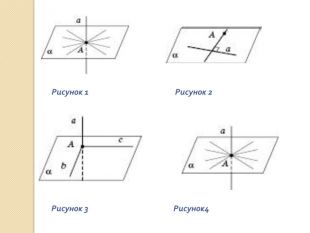
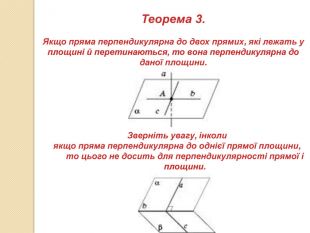
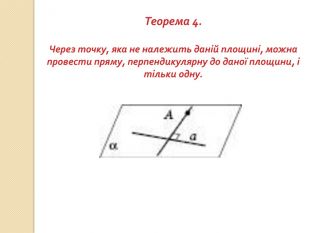
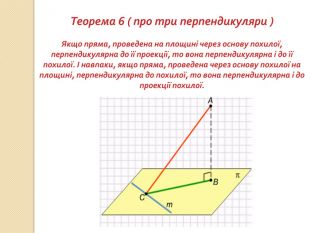
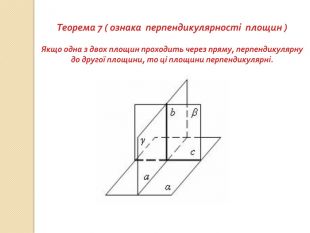
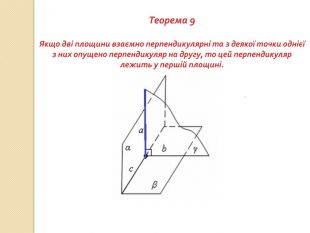
презентация "Перпендикулярність у просторі"
Про матеріал
під час карантину презентация допоможе учням повторити тему и запам'ятати важливи висновки Перегляд файлу
Зміст слайдів
pptx
До підручника
Геометрія (профільний рівень) 10 клас (Бевз В.Г., Бевз Г.П., Владімірова Н.Г., Владіміров В.М.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку