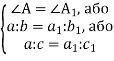Посібник для уроків геометрії ІІ семестр 8 класу

Про матеріал

Дана розробка може бути використана як додаток до уроків геометрії у ІІ семестрі 8 класу, як роздатковий матеріал учням. Укладена згідно Комбінованої системи М.П. Гузика

Перегляд файлу

Шановні восьмикласники!

Ви продовжуєте вивчати геометрію. А сприяти вам буде навчальний посібник, який ви тримаєте в руках.

Посібник складається з трьох тем. Кожна тема має таку структуру:

перший урок – урок розбору блоку навчальної інформації;
наступні уроки – уроки фронтального опрацювання матеріалу, на яких проводиться робота з засвоєння понять, термінів і правил блоку навчальної інформації, також наведені вправи і завдання для відпрацювання практичних умінь і навичок.
між уроками фронтального опрацювання ви будете виконувати завдання індивідуального опрацювання матеріалу, вправи якого не наведені в даному посібнику. Але він містить завдання для підготовки до індивідуального опрацювання, позначені

в кінці кожної теми є один урок внутрішньопредметного узагальнення матеріалу, на якому кожен покаже свої знання блоку, а також узагальнить знання і вміння, здобуті під час теми.

Також в кінці посібника є повторення всього матеріалу, який ми вивчали протягом року.

Нехай Бог посилає вам мудрості у вивченні геометрії!!!

Тема №4. Застосування подібності трикутників

Урок №1

Застосування подібності трикутників

Геометричні уявлення людина дістає за допомогою своїх

почуттів до того, як вона матиме про них цілком визначене поняття

М. Є. Ващенко – Захаренко

Питання

Ознаки подібності прямокутних трикутників.
Застосування подібності трикутників.

Література

Істер О.С. Геометрія: підручник для 8-го класу загальноосвітніх навчальних закладів, К.: Ґенеза, 2016 рік, § 14– 17, стор. 87 – 118.

Ознаки подібності прямокутних трикутників
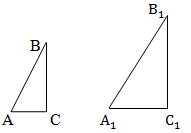
1.1	Два прямокутні трикутники подібні, якщо гострий кут одного трикутника дорівнює гострому куту другого трикутника.
1.2	Два прямокутні трикутники подібні, якщо катети одного пропорційні катетам другого трикутника.
1.3	Два прямокутні трикутники подібні, якщо катет і гіпотенуза одного пропорційні катету і гіпотенузі другого трикутника.
1.4	Висота прямокутного трикутника, проведена до гіпотенузи, розбиває даний трикутник на два менші прямокутні трикутники, подібні даному.
Застосування подібності трикутників.
2.5	Теорема *Бісектриса трикутника ділить протилежну сторону на відрізки, пропорційні прилеглим сторонам.*
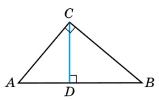
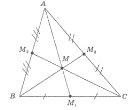
2.6	Теорема Усі три медіани трикутника проходять через одну точку і діляться цією точкою у відношенні 2:1, починаючи від вершини трикутника.
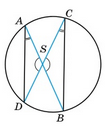
2.7	Теорема *Добутки відрізків хорд одного кола, що перетинаються, рівні.* АS · ВS = СS · DS
2.8	Число називається середнім пропорційним між числами , якщо .
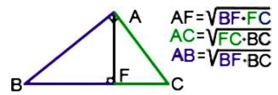
2.9	Теорема Висота прямокутного трикутника, проведена до гіпотенузи, є середнім пропорційним відрізків, на які ця висота ділить гіпотенузу.
2.10	Відрізки, на які висота ділить гіпотенузу, називаються проекціями катетів на гіпотенузу. АС – проекція АD ВС – проекція ВD
2.11	Теорема *Катет прямокутного трикутника є середнім пропорційним гіпотенузи і проекції цього катета на гіпотенузу.*

Уроки №2,3

«Люди – єдині істоти на землі, які потребують

допомоги Бога, але ведуть себе так, ніби Бога немає»

Джоні Депп

Фронтальне опрацювання матеріалу

Подібність прямокутних трикутників. Середні пропорційні відрізки у прямокутному трикутнику

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 1.1 – 1.4, 2.8 – 2.11 блоку № 4.
Усно дай відповідь на питання:

Сформулюй ознаки подібності прямокутних трикутників.
Що робить з даним прямокутним трикутником висота, проведена до гіпотенузи?
Яке число називається середнім пропорційним між числами a і b?
Що називають проекціями катетів на гіпотенузу?
Яку властивість має висота прямокутного трикутника, проведена до гіпотенузи?
Яку властивість має катет прямокутного трикутника?

Завдання 2.

Усно виконати вправи, запропоновані учителем (презентація).

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 3.

Письмово виконай вправи:

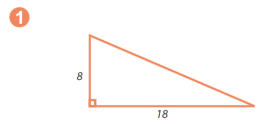
Катет прямокутного трикутника дорівнює 8 см, а його проекція на гіпотенузу – 4 см. Знайдіть гіпотенузу.
Один з катетів прямокутного трикутника дорівнює 4 см, а проекція другого катета на гіпотенузу – 6 см. Знайдіть другий катет і гіпотенузу.
Знайдіть периметр прямокутного трикутника, висота якого ділить гіпотенузу на відрізки завдовжки 4,5 см і 8 см.

ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач

Завдання 4.

Письмово виконай вправи:

Висота дерева дорівнює 9,2 м, а довжина тіні людини, зріст якої 1,8 м дорівнює 2,7 м. Знайдіть довжину тіні дерева.
Перпендикуляр, проведений з точки перетину діагоналей ромба до його сторони, ділить сторону ромба на відрізки завдовжки 4 см і 25 см. Знайдіть діагоналі ромба.
Діагональ рівнобічної трапеції перпендикулярна до бічної сторони і дорівнює 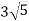см, а проекція бічної сторони на більшу основу дорівнює 4 см. Знайдіть основи трапеції та її бічну сторону.

Урок №4

«Що може бути шкідливіше за людину, котра

володіє знанням найскладніших наук, але не має доброго серця?»

Григорій Сковорода

Фронтальне опрацювання матеріалу

Застосування подібності трикутників

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори блок № 4.
Усно дай відповідь на питання:

Сформулюй ознаки подібності прямокутних трикутників.
Що робить з даним прямокутним трикутником висота, проведена до гіпотенузи?
Яке число називається середнім пропорційним між числами a і b?
Що називають проекціями катетів на гіпотенузу?
Яку властивість має висота прямокутного трикутника, проведена до гіпотенузи?
Яку властивість має катет прямокутного трикутника?
Сформулюй властивість бісектриси трикутника.
Сформулюй властивість медіан трикутника.
Сформулюй властивість відрізків хорд одного кола, що перетинаються.

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 2.

Усно виконати вправи:

Назви подібні трикутники, зображені на малюнку .

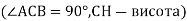А	Б	В	Г

Знайди висоту прямокутного трикутника, проведену до гіпотенузи, якщо вона ділить гіпотенузу на відрізки 4 см і 9 см.

А	Б	В	Г
6 см	13 см	36 см	см

Медіана трикутника дорівнює 12 см. Знайди довжини відрізків, на які вона ділиться точкою перетину медіан.

А	Б	В	Г
6 см і 6 см	8 см і 4 см	9 см і 3 см	10 см і 2 см

Завдання 3.

Письмово виконай вправи:

Знайди катет прямокутного трикутника, якщо його гіпотенуза дорівнює 20 см, а проекція цього катета на гіпотенузу 5 см.
Висота прямокутного трикутника, проведена до гіпотенузи, ділить її на відрізки 18 см і 32 см. Знайди катети трикутника.

Хорди MN і EF перетинаються в точці К, яка ділить хорду MN навпіл. Знайди MN, якщо КЕ = 4 см, KF = 16 см.
Перпендикуляр, проведений з точки перетину діагоналей ромба до його сторони, ділить сторону ромба на відрізки завдовжки 2,25 см і 4 см. Знайди діагоналі ромба

ІІІ. Відпрацювання умінь розв’язування нестандартних вправ

Завдання 4.

Письмово виконай вправу:

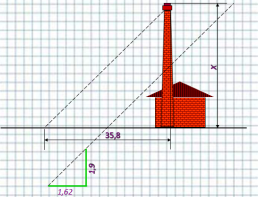
Довжина тіні фабричної труби дорівнює 35,8 м. У той самий час вертикально поставлена жердина завдовжки 1,9 м дає тінь довжиною 1,62 м. Знайдіть висоту труби.

&Kcy;&acy;&rcy;&tcy;&icy;&ncy;&kcy;&icy; &pcy;&ocy; &zcy;&acy;&pcy;&rcy;&ocy;&scy;&ucy; &kcy;&acy;&rcy;&tcy;&icy;&ncy;&kcy;&icy; &zcy;&ncy;&acy;&kcy; &vcy;&ocy;&scy;&kcy;&lcy;&icy;&tscy;&acy;&ncy;&icy;&yacy;

Готуємось до індивідуального опрацювання

Знайди катет прямокутного трикутника, якщо його гіпотенуза дорівнює 12 см, а проекція цього катета на гіпотенузу 3 см.

А	Б	В	Г
36 см	15 см	6 см	9 см

Висота прямокутного трикутника, проведена до гіпотенузи, ділить її на відрізки 3 см і 12 см. Знайди катети трикутника.
Хорди MN і EF перетинаються в точці К, яка ділить хорду MN навпіл. Знайди MN, якщо КЕ = 5 см, KF = 20 см.
Перпендикуляр, проведений з точки перетину діагоналей ромба до його сторони, ділить сторону ромба на відрізки завдовжки 8 см і 50 см. Знайди діагоналі ромба.

Урок №6

«Загублений той час,

який ти не використав на навчання»

Пліній, історик Стародавнього Риму

Внутрішньопредметне узагальнення матеріалу

Застосування подібності трикутників

І. Систематизація та узагальнення теоретичних знань

Завдання 1.

Повтори блок № 4.
Дай письмово відповідь на питання, запропоновані вчителем.

ІІ. Систематизація та узагальнення практичних умінь та навичок

Завдання 2.

Усно розв’яжи вправи:

Яке з наведених тверджень неправильне?

А	Б	В	Г
Бісектриса трикутника ділить протилежну сторону на відрізки, пропорційні двом іншим сторонам	Якщо гострий кут одного прямокутного трикутника дорівнює гострому куту другого прямокутного трикутника, то такі трикутники подібні	Висота прямокутного трикутника, проведена з вершини прямого кута, є середнім пропорційним між гіпотенузою і проекцією катета на гіпотенузу	Якщо сторони одного трикутника пропорційні сторонам другого трикутника, то такі трикутники подібні

Точка К поділяє відрізок СD на відрізки CК = 6 см і КD = 4 см. Знайдіть відношення КC:CD

А	Б	В	Г
0,6см	2	0,4	0,6

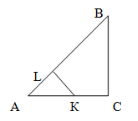
Назвіть подібні трикутники, зображені на рисунку, якщо .

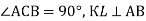А	Б	В	Г

Завдання 3.

Письмово виконай вправи:

Знайти висоту прямокутного трикутника, проведену до гіпотенузи, якщо проекції катетів на гіпотенузу дорівнюють 16 см і 64 см.
Знайти катет прямокутного трикутника, якщо його проекція на гіпотенузу дорівнює 25 см, а гіпотенуза – 64 см.
Висота прямокутного трикутника, проведена до гіпотенузи, дорівнює 4 см, а проекція одного з катетів на гіпотенузу – 6 см. Знайти гіпотенузу.
Продовження бічних сторін АВ і СD трапеції ABCD перетинаються в точці F, AB:BF=3:7, ВС – менша основа трапеції. Знайдіть основи трапеції, якщо їх різниця дорівнює 12 см.
Діагональ рівнобічної трапеції перпендикулярна до бічної сторони. Основи трапеції дорівнюють 15 см і 39 см. Знайдіть висоту, бічну сторону і діагональ трапеції.

Тема №5. Розв’язування прямокутних трикутників

Урок №1

Розв’язування прямокутних трикутників

«Золоті яблука на срібнім

тарелі – це слово, проказане часу свого»

Книга приповістей Соломонових 25:11

Питання

Теорема Піфагора.
Перпендикуляр і похила.
Синус, косинус і тангенс гострого кута прямокутного трикутника.
Розв’язування прямокутних трикутників.

Література

Істер О.С. Геометрія: підручник для 8-го класу загальноосвітніх навчальних закладів, К.: Ґенеза, 2016 рік, § 18– 21, стор. 119 – 154.

1. Теорема Піфагора

1.1

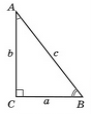
Теорема Піфагора. У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.

В С

1.2

Теорема (обернена теоремі Піфагора). Якщо у трикутнику АВС , то кут В цього трикутника прямий.

2. Перпендикуляр і похила

2.3

Якщо відрізок АС, кінець С якого належить прямій а, перпендикулярний до прямої а, то його називають перпендикуляром, проведеним з точки А до прямої а.

С В

АС – перпендикуляр

С – основа перпендикуляра

АВ – похила

В – основа похилої

ВС – проекція похилої на пряму а

2.4

Відрізок, проведений з тієї ж точки, але відмінний від перпендикуляра, називається похилою, проведеною з точки А до прямої а.

2.5

Відрізок між основою перпендикуляра і основою похилої, проведених з однієї точки, називається проекцією похилої на пряму.

2.6

Властивості похилої і перпендикуляра:

1) перпендикуляр, проведений з точки до прямої, менший від будь-якої похилої, проведеної з цієї точки до цієї прямої;

2) якщо дві похилі, проведені з точки до прямої, рівні між собою, то рівні між собою і їх проекції;

3) якщо проекції двох похилих, проведених з точки до прямої рівні між собою, то рівні між собою і самі похилі;

4) з двох похилих, проведених з точки до прямої, більшою є та, у якої більша проекція;

5) з двох похилих, проведених з точки до прямої, більша похила має більшу проекцію.

С В

3. Синус косинус і тангенс гострого кута прямокутного трикутника

3.7

Синусом гострого кута прямокутного трикутника називається відношення протилежного катета до гіпотенузи.

See – з англійської «дивитися, бачу»

3.8

Косинусом гострого кута прямокутного трикутника називається відношення прилеглого катета до гіпотенузи.

3.9

Тангенсом гострого кута прямокутного трикутника називається відношення протилежного катета до прилеглого.

3.10

Значення синуса, косинуса і тангенса деяких кутів

α	30°	45°	60°
*sin* α
*cos*α
tgα		1

4. Розв’язування прямокутних трикутників

4.11

Розв’язати трикутник – означає знайти невідомі його сторони і кути за відомими сторонами і кутами

4.12

Катет прямокутного трикутника дорівнює добутку:

1) гіпотенузи на синус протилежного кута;

2) гіпотенузи на косинус прилеглого кута;

3) другого катета на тангенс протилежного кута.

4.13

Гіпотенуза прямокутного трикутника дорівнює частці від ділення:

1) катета на синус протилежного кута;

2) катета на косинус прилеглого кута.

Уроки №2,3

«Геометрія володіє двома

скарбами: один з них – це теорема Піфагора»

Йоган Кеплер

Фронтальне опрацювання матеріалу

Теорема Піфагора

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 1.1 – 1.2 блоку № 5.
Познайомся з біографією Піфагора (презентація вчителя).
Усно дай відповідь на питання:

Як читається теорема Піфагора?
Як читається теорема, обернена до теореми Піфагора?
1. Розглянь найпростіший спосіб доведення теореми Піфагора (презентація).

Завдання 2.

Усно розв’яжи задачі за готовими малюнками (презентація).

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 3.

Письмово виконай вправи:

3.1. Складність 1.

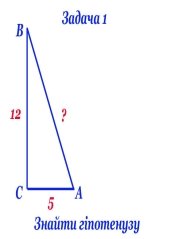
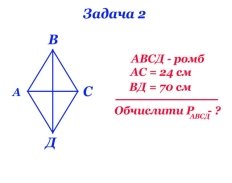
зад_01 зад_02

3.2. Складність 2.

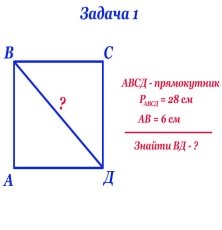
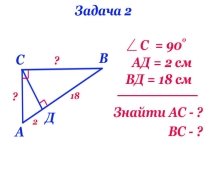
зад_02_01 зад_02_02

ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ

Завдання 4.

Письмово виконай вправи:

Один за катетів прямокутного трикутника дорівнює 6 см, а проекція другого катета на гіпотенузу дорівнює 5 см. Знайди другий катет.
Проекції катетів на гіпотенузу дорівнюють 12 см і 27 см. Знайди катети.

Завдання 5.

Розв’яжи історичні задачі:

Завдання з підручника "Арифметика" Леонтія Магницького: "Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обретете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать."
Для кріплення щогли потрібно встановити 4 мотузки. Один кінець кожної мотузки повинен кріпитися на висоті 12 м, другий – на землі на відстані 5 м від щогли. Чи вистачить 50 м мотузки для кріплення щогли?
Завдання індійського математика XII століття Бхаскари:

"На березі річки тополя самотня.

Раптом вітру порив її стовбур зламав.

Тополя впала. І кут прямий

З поверхнею річки її стовбур склав.

Тепер пам'ятай, що в тім місці річка

В чотири лиш фути була шириною

Верхівка схилилася до краю річки.

Лишились три фути всього висотою.

Прошу тебе, дай мені відповідь ту,

Яку у тополі знайшов висоту?"

Уроки №4,5

«Хто уста свої стереже, той душу свою береже»

Книга приповістей Соломонових 13:3

Фронтальне опрацювання матеріалу

Перпендикуляр і похила

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 1.1 – 2.6 блоку № 5.
Усно дай відповідь на питання:

Як читається теорема Піфагора?
Як читається теорема, обернена до теореми Піфагора?
Що називається перпендикуляром, опущеним з точки на пряму?
Що називається похилою?
Що називається проекцією похилої на пряму?
Які властивості мають перпендикуляр і похила?

Завдання 2.

Усно розв’яжи вправи, стор. 131 підручника: 683.

Завдання 3.

Усно розв’яжи вправи:

Яке з наведених тверджень неправильне?

А	Б	В	Г
У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів	Гіпотенуза прямокутного трикутника більша за кожен з його катетів	Із двох похилих більша та, у якої проекція більша	Квадрат катета дорівнює сумі квадратів гіпотенузи та іншого катета

Катети прямокутного трикутника дорівнюють 8 см і 15 см. Знайди гіпотенузу.

А	Б	В	Г
	23см	17см	18см

Знайди катет прямокутного трикутника, у якому гіпотенуза та інший катет дорівнюють відповідно 9 см і 5 см.

А	Б	В	Г
2см	26см	10см	18см

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 4.

Письмово виконай вправи:

З точки до прямої проведено дві похилі. Довжина однієї з них дорівнює 25 см, а довжина її проекції на цю пряму дорівнює 15 см. Знайди довжину другої похилої, якщо вона утворює з прямою кут 30º.
З точки, яка знаходиться на відстані 5 см від прямої, проведено до неї дві похилі. Довжина однієї з них дорівнює 13 см, а друга утворює з прямою кут 45º. Знайди відстань між основами похилих.
З точки до прямої проведено дві похилі, проекції яких на цю пряму дорівнюють 5 см і 9 см. Знайди довжини похилих, якщо їх різниця дорівнює 2 см.
З точки до прямої проведено дві похилі, довжини яких дорівнюють 10 см і 6 см, а довжини їх проекцій на цю пряму відносяться як 5:2. Знайди відстань від точки до даної прямої.

Завдання 5.

Письмово розв’язати вправи:

Сторони прямокутника дорівнюють 24 см і 32 см. Знайди довжину діагоналей прямокутника.
Бічна сторона рівнобедреного трикутника дорівнює 58 см, а його висота, що проведена до основи, – 42см. Знайди основу трикутника.
З точки В до прямої проведено дві похилі ВА = 10 см і ВС = 7 см. Проекція похилої ВА дорівнює 8 см. Знайди проекцію похилої ВС.

ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ

Завдання 6.

Сума катетів прямокутного трикутника дорівнює 17 см, а гіпотенуза – 13 см. Знайди невідомі сторони трикутника.
У рівнобічній трапеції діагональ утворює прямий кут з бічною стороною і дорівнює 15 см, а висота трапеції – 12 см. Знайди середню лінію трапеції.

Готуємось до індивідуального опрацювання

Сторони прямокутника дорівнюють 9см і 12см. Знайди довжину діагоналей прямокутника.
Бічна сторона рівнобедреного трикутника дорівнює 26см, а його висота, що проведена до основи, – 10см. Знайди основу трикутника.
З точки А до прямої проведено дві похилі АВ і АС, АВ = 20см. Проекція похилої АС дорівнює 8см, проекція похилої АВ – 16см. Знайди похилу АС.
Різниця між гіпотенузою і катетом прямокутного трикутника 4см, а довжина другого катета – 8см. Знайди невідомі сторони трикутника.
У рівнобічній трапеції діагональ утворює прямий кут з бічною стороною і дорівнює 30см, а висота трапеції – 18см. Знайди середню лінію трапеції.

Урок №7

«Бо Господь дає мудрість, з Його уст знання й розум»

Книга приповістей Соломонових 2:6

Фронтальне опрацювання матеріалу

Синус, косинус і тангенс гострого кута прямокутного трикутника

І. Робота над засвоєнням понять, означень, правил

Завдання 1.

Повтори тези 3.7 – 3.11 блоку № 5.
Усно дай відповідь на запитання:

Як називаються сторони прямокутного трикутника?
Що називають косинусом гострого кута прямокутного трикутника?
Що таке синус гострого кута прямокутного трикутника?
Сформулюй означення тангенса гострого кута прямокутного трикутника.
Чому дорівнює катет прямокутного трикутника?
Як знайти гіпотенузу прямокутного трикутника?

Завдання 2.

Усно виконай вправи:

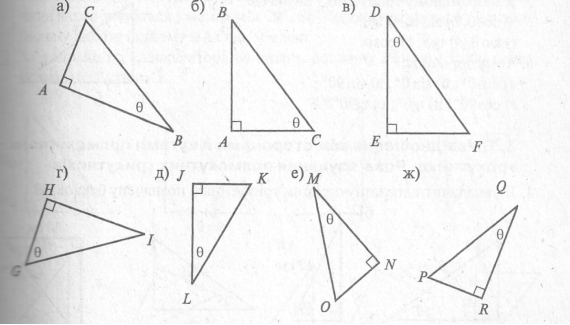
Для кожного із зображених трикутників назви: 1) гіпотенузу; 2) катет, прилеглий до кута 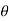; 3) катет, протилежний куту .

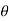$C:\Users\олеся\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\1.tif$

У прямокутному трикутнику АВС (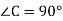) АВ = 5см, . Знайти ВС. А

А	Б	В	Г

С В

Дано Δ АВС, 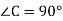. Яке з даних чисел є тангенсом кута В, якщо АВ = 5, АС = 3, ВС = 4?

А	Б	В	Г

С В

ІІ. Відпрацювання умінь і навичок, застосування правил

Завдання 3.

Письмово розв’яжи задачі за готовими малюнками:

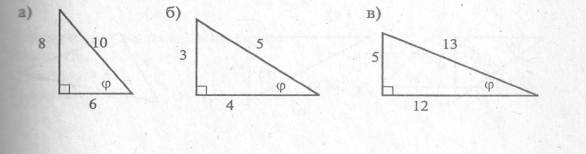
Знайди значення 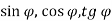для кожного із зображених трикутників.

$C:\Users\олеся\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\1.tif$

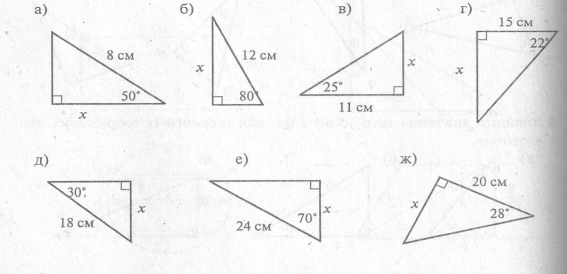$C:\Users\олеся\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\2.tif$ Визнач довжину сторони трикутника, позначену буквою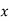

Завдання 4.

Письмово розв’яжи вправи:

Висота рівнобедреного трикутника, проведена до основи, дорівнює 5 см, а довжина основи 24 см. Знайди синус, косинус, тангенс кута при основі трикутника.
У прямокутному трикутнику АВС 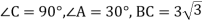. Знайди АС.
Знайди усі тригонометричні функції кута при основі рівнобедреного трикутника, основа якого дорівнює 20см, бічна сторона – 26см.

Урок №8

«Не відкладайте на завтра те,

що можна зробити сьогодні»
Бенджамін Франклін

Фронтальне опрацювання матеріалу

Властивості тригонометричних функцій

І. Робота над засвоєнням понять, означень, правил

Завдання 1.

Повтори тези 3.7 – 3.13 блоку № 5.
Усно дай відповідь на запитання:

Що називають косинусом гострого кута прямокутного трикутника?
Що таке синус гострого кута прямокутного трикутника?
Сформулюй означення тангенса гострого кута прямокутного трикутника.
Як можна знайти катет прямокутного трикутника?
Чому дорівнює гіпотенуза прямокутного трикутника?
Які властивості мають тригонометричні функції гострого кута прямокутного трикутника?

Завдання 2.

Усно виконай вправи, стор. 138 підручника: 711; 712.

ІІ. Відпрацювання умінь і навичок, застосування правил

Завдання 3.

Письмово виконай вправи, стор. 139 – 205 підручника: 715; 721 (1, 3); 723 (1); 737; 739 (1).

Уроки №9 – 11

«Ні про що не турбуйтесь, а в усьому нехай виявляються

Богові ваші бажання молитвою й проханням з подякою»

Послання ап. Павла до филипʼян 4:6

Фронтальне опрацювання матеріалу

Співвідношення між сторонами і кутами прямокутного трикутника. Розв’язування прямокутних трикутників. Прикладні задачі

І. Робота над засвоєнням понять, означень, правил

Завдання 1.

Повтори тези 3.7 – 3.13 блоку № 5.
Усно дай відповідь на запитання:

Що називають косинусом гострого кута прямокутного трикутника?
Що таке синус гострого кута прямокутного трикутника?
Сформулюй означення тангенса гострого кута прямокутного трикутника.
Як можна знайти катет прямокутного трикутника?
Чому дорівнює гіпотенуза прямокутного трикутника?
Які властивості мають тригонометричні функції гострого кута прямокутного трикутника?
Що означає розв’язати трикутник?

Завдання 2.

Усно розв’яжи вправи:

Знайди значення виразу .

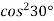А	Б	В	Г

У прямокутному трикутнику АВС (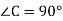) АВ = 5см, 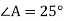. Знайди ВС. А

С В

Яке з даних чисел є тангенсом кута В, якщо АВ = 5, АС = 3, ВС = 4?

А	Б	В	Г

С В

ІІ. Відпрацювання умінь і навичок, застосування правил

Завдання 3.

3.1. Письмово виконай вправи, стор. 146 підручника: 756 (1, 3); 758 (2, 4).

3.2. У прямокутному трикутнику катети відносяться як 12 до 5, а гіпотенуза 39см. Знайти катети.

Письмово виконай вправи:

Завдання 4.

Знайди усі тригонометричні функції кута при основі рівнобедреного трикутника основа якого дорівнює 20см, бічна сторона – 26см.
У рівнобічній трапеції АВСD основи АD і ВС відповідно дорівнюють 8см і 12см, а бічна сторона утворює кут 30° з основою. Знайди висоту і бічну сторону трапеції.

Завдання 5.

З точки, що знаходиться на відстані 12 см від прямої, проведено до неї дві похилі, які утворюють з прямою кути 45º і 60º. Знайди довжини похилих і їх проекцій на пряму.
З точки, що знаходиться на відстані 8 см від прямої, проведено до неї дві похилі, які утворюють з прямою кути 30º і 45º. Знайди відстань між основами похилих. Скільки розв’язків має задача?

ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ

Завдання 6.

6.1. Висоти двох вертикальних стовпів дорівнюють 5м і 12,5м. Відстань між ними 10м. Знайти найменшу довжину троса, яким можна з’єднати верхні кінці стовпів?

6.2. У трикутнику АВС висота ВD поділяє сторону АС на відрізки АD і DС. , , . Знайдіть сторону АС трикутника.

З точки, що знаходиться на відстані 8см від прямої, проведено до неї дві похилі, які утворюють з прямою кути 45^о і 60^о . Знайдіть відстань між основами похилих. Скільки розв’язків має задача?

Готуємось до індивідуального опрацювання

У прямокутному трикутнику АВС 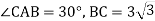. Знайди АС.
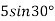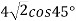Обчисли: 1) ; 2) ; 3) .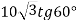
Знайди усі тригонометричні функції кута при основі рівнобедреного трикутника основа якого дорівнює 18 см, бічна сторона – 15 см.
З точки, що лежить на відстані 16 см від прямої, проведено дві похилі, які утворюють з прямою кути 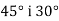. Знайди довжини похилих і їх проекцій на пряму.

Урок №13

«… моліться за тих, хто вас переслідує»

Матвія 5:44

Внутрішньопредметне узагальнення матеріалу

Розв’язування прямокутних трикутників

І. Систематизація та узагальнення теоретичних знань

Завдання 1.

Повтори блок № 5.
Дай письмово відповідь на питання, запропоновані вчителем.

ІІ. Систематизація та узагальнення практичних умінь та навичок

Завдання 2.

Усно виконати вправи:

Катети прямокутного трикутника дорівнюють 12см і 9см. Знайдіть гіпотенузу.

А	Б	В	Г
см	3см	9см	15см

Яке з наведених тверджень неправильне?

А	Б	В	Г
У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів	Гіпотенуза прямокутного трикутника більша за кожен з його катетів	Із двох похилих, що проведені з однієї точки, більша та, у якої проекція більша	Квадрат катета дорівнює сумі квадратів гіпотенузи та іншого катета

Яке з наведених тверджень правильне?

А	Б	В	Г
Косинусом гострого кута називається відношення протилежного катета до прилеглого	Косинусом гострого кута називається відношення прилеглого катета до гіпотенузи	Косинусом гострого кута називається відношення протилежного катета до гіпотенузи	Косинусом гострого кута називається відношення прилеглого катета до протилежного

Завдання 3.

Письмово розв’яжіть вправи:

У прямокутному трикутнику катети дорівнюють 4см і 3см. Знайдіть периметр трикутника.
Знайдіть значення виразу .
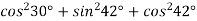З точки до прямої проведено дві похилі, довжини яких дорівнюють 3см і 4см. Знайдіть відстань від точки до прямої, якщо різниця проекцій похилих на цю пряму дорівнює 2см.
У рівнобічній трапеції АВСD основи АD і ВС відповідно дорівнюють 4см і 6см, а бічна сторона утворює кут 30° з основою. Знайти висоту, бічну сторону трапеції.

Тема №6. Многокутники. Площі многокутників

Урок №1

Многокутники. Площі многокутників

«Геометрія – це мистецтво добре вимірювати»

П’єр Раме, французький філософ, математик

Питання

Ламана.
Многокутники.
Вписані й описані многокутники.
Площі многокутників.

Література

Істер О.С. Геометрія: підручник для 8-го класу загальноосвітніх навчальних закладів, К.: Ґенеза, 2016 рік, § 22– 26, стор. 155 – 186.

1. Ламана
1.1	Ламаною називається фігура, яка складається з точок (вершини ламаної), послідовно сполучених відрізками (ланки ламаної).	Проста D А В С Е Із самоперетином Замкнена
1.2	Ламана називається простою, якщо вона не має самоперетинів і ніякі дві її сусідні ланки не лежать на одній прямій.
1.3	Ламана називається замкненою, якщо її кінці збігаються.
1.4	Довжиною ламаної називають суму довжин усіх її ланок.
2. Многокутники
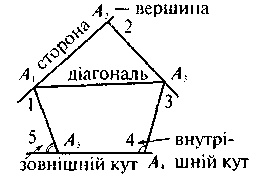
2.5	Многокутником називається проста замкнена ламана. Дві вершини, які є кінцями однієї сторони називають сусідніми вершинами.
2.6	Відрізок, який сполучає несусідні вершини многокутника, називається діагоналлю.
2.7	Кутом (внутрішнім) многокутника при даній вершині називається кут між його сторонами, які сходяться в цій вершині.
2.8	Зовнішнім кутом многокутника при даній вершині називається кут, суміжний із внутрішнім кутом многокутника при цій вершині.
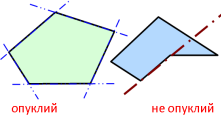
2.9	Многокутник називається опуклим, якщо всі його кути менші від розгорнутого.
2.10	Сума кутів опуклого п – кутника дорівнює 180°(п – 2).
2.11	Сума зовнішніх кутів, взятих по одному при кожній вершині довільного многокутника, дорівнює 360°.
2.12	Периметром многокутника називається сума довжин усіх його сторін.
2.13	Многокутник, у якого рівні всі сторони та всі кути, називається правильним.
3. Вписані та описані многокутники
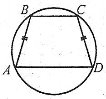
3.14	Якщо всі вершини многокутника лежать на колі, його називають вписаним у коло, а коло – описаним навколо многокутника.
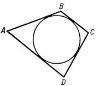
3.15	Якщо всі сторони многокутника дотикаються до кола, його називають описаним навколо кола, а коло – вписаним у многокутник.
3.16	Навколо кожного правильного многокутника можна описати коло і тільки одне. У кожний правильний многокутник можна вписати коло і тільки одне.
4. Площі многокутників
4.17	Площа многокутника – це величина, що має такі властивості: 1) площа виражається додатним числом; 2) рівні многокутники мають рівні площі; 3) площа многокутника, складеного із кількох частин дорівнює сумі площ цих частин; 4) за одиницю площі приймається площа одиничного квадрата ( квадрат, сторона якого дорівнює одиниці довжини).
4.18	Площа прямокутника зі сторонами a i b дорівнює:
4.19	Якщо сторона квадрата дорівнює а, то його площа
4.20	Площа паралелограма дорівнює добутку його основи на висоту, проведену до цієї основи:
4.21	Площа трапеції дорівнює добутку півсуми її основ на висоту:
4.22	Площа ромба дорівнює півдобутку діагоналей:
4.23	Площа трикутника дорівнює півдобутку його сторони на висоту проведену до цієї сторони:
4.24	Площа прямокутного трикутника дорівнює півдобутку його катетів:
4.25	Площа правильного трикутника: .
4.26	Площа будь – якого трикутника обчислюється за формулою Герона , де р – півпериметра, a,b,c – сторони
4.27	Площа многокутника, описаного навколо кола, обчислюється за формулою де р – півпериметра, r – радіус вписаного кола.

Урок №2

«Люди – єдині істоти на землі, які потребують

допомоги Бога, але ведуть себе так, ніби Бога немає»

Джоні Депп, американський актор, продюсер, музикант

Фронтальне опрацювання матеріалу

Многокутник та його елементи. Опуклі та неопуклі многокутники. Сума кутів опуклого многокутника

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 1.1 – 2.13 блоку № 6.
Усно дай відповідь на питання:

Що називають ламаною?
Яка ламана називається простою?
Яка ламана називається замкненою?
Чому дорівнює довжина ламаної?
Що називають многокутником?
Що таке діагональ многокутника?
Що називають кутом многокутника?
Що називають зовнішнім кутом многокутника?
Який многокутник називається опуклим?
Чому дорівнює сума кутів опуклого п – кутника?
Чому дорівнює сума зовнішніх кутів многокутника, взятих по одному при кожній вершині?
Що називають периметром многокутника?
Який многокутник називається правильним?

Завдання 2.

Усно виконай вправи, стор. 158 підручника: 810.
Знайди суму кутів опуклого: а) шестикутника; б) дванадцятикутника.
Розглянь задачу 1, стор.156 підручника. Запиши формулу для визначення кількості діагоналей опуклого п – кутника у блок і запам’ятай її.

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 3.

Письмово виконай вправи:

Стор. 159 підручника: 822; 828.
Визначте кількість сторін опуклого многокутника, сума кутів якого дорівнює: а) 540; б) 900.
Визначте, чи існує опуклий многокутник, сума кутів якого дорівнює: а)1620; б) 1980; в) 1350.
Визначте кількість сторін опуклого многокутника, кожен кут якого дорівнює: а) 60; б) 120.

Урок №3

«Хто шукає - той знайде, хто стукає - тому відкриють»

Євангеліє від св. Луки 11:9

Фронтальне опрацювання матеріалу

Вписані і описані многокутники

І. Робота над засвоєнням понять, термінів і правил

Завдання 1

Уважно прочитай тези 1.1 – 3.16 блоку № 6.
Усно вставте пропущені слова у визначення і правила:

Ламаною називається фігура, яка складається …
… називається проста замкнена ламана.
Сума кутів опуклого многокутника дорівнює …
Якщо всі вершини многокутника лежать на колі, його називають …
… називають описаним навколо кола.

Завдання 2

2.1. Усно дай відповіді на запитання:

Де лежить центр кола, описаного навколо трикутника? (7 клас)
Де лежить центр кола, вписаного в трикутник? (7 клас)
Навколо якого чотирикутника можна описати коло?
В який чотирикутник можна вписати коло?
1. Усно виконай вправи, стор. 159 підручника: 815.

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 3

Письмово виконай вправи, стор. 160 підручника: 829, 830.

Знайдіть кути опуклого семикутника, якщо їх градусні міри відносяться як 2:5:3:9:7:6:4.

Один з кутів опуклого шестикутника дорівнює 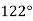, другий, третій, четвертий і п’ятий відносяться як 8:6:4:3, а шостий дорівнює піврізниці другого і четвертого кутів. Знайдіть невідомі кути шестикутника.

Уроки №4 – 6

«Усе перевіряйте, чи воно

правильне, міцно тримайтесь того, що добре»

1 послання ап. Павла до солунян 5:21

Фронтальне опрацювання матеріалу

Площі многокутників

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Уважно прочитай тези 4:17 – 4.27 блоку № 6.
Усно продовж речення:

Площа прямокутника дорівнює…
Площа квадрата ….
Площа паралелограма ….
Площа трапеції…
Площа ромба…
Площа трикутника…
Площа прямокутного трикутника…
Формула Герона …

Завдання 2.

Усно розв’яжи вправи:

Обчисли площу квадрата зі стороною 0,7 м.

А	Б	В	Г
0,49 м²	48 дм ²	36 дм ²	1,8 м²

Обчисли площу паралелограма зі стороною 10 см і висотою 6 см, проведеною до цієї сторони.

А	Б	В	Г
16 см ²	30 см ²	60 см ²	м

Обчисли площу трапеції з основами 9 см і 7 см та висотою 3 см.

А	Б	В	Г
24см	185см²	56см²	24см²

Виконай усно вправи 843, 845 стор. 163 підручника.

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 3.

Письмово виконати вправи:

Обчисли площу квадрата, периметр якого дорівнює 48 см.
Знайди площу прямокутного трикутника, катети якого дорівнюють 12 см і 9 см.
Діагоналі ромба дорівнюють 12 см і 7 см. Обчисли його площу.
Одна із сторін паралелограма дорівнює 12 см, а висота, проведена до другої сторони, – 24 см. Знайди невідомі сторону та висоту паралелограма, якщо його площа дорівнює 96 см².
Площа трапеції дорівнює 168 см², одна з її основ – 20 см, а висота – 12 см. Знайди другу основу трапеції.
Знайди площу прямокутного трикутника, якщо висота, проведена до гіпотенузи, поділяє її на відрізки завдовжки 4 см і 16 см.

Завдання 4.

Виконати самостійно завдання:

Дано певні виміри трикутника. Вам необхідно знайти площі цих трикутників.

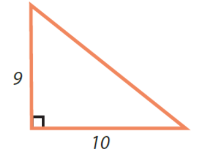Приклад:

Перший катет: 10 см.

Другий катет: 9 см.

Площа трикутника: .

Перший катет: _________________ см

Другий катет: __________________ см

Площа трикутника: ________________

_________________________________

Сторона: _________________ см

Висота: __________________ см

Площа трикутника: ________________

_________________________________

Перший катет: _________________ см

Другий катет: __________________ см

Площа трикутника: ________________

_________________________________

Сторона: _________________ см

Висота: __________________ см

Площа трикутника: ________________

_________________________________

Виконайте кросворд. Ключове слово кросворда ви прочитаєте у виділеному стовпчику

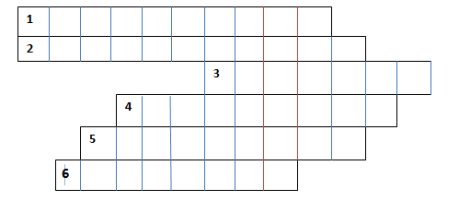
Сторона прямокутного трикутника
Паралелограм з прямими кутами
Фігура з рівними сторонами
У чотирикутнику живуть,

Із кута у протилежний кут ідуть

Ми їх в задачах зустрічаємо.

І як ми ці відрізки називаємо?

Три точки невеличкі

Відрізками сполучимо.

А те, що утворилось,

Всі разом озвучимо.

Геометрична фігура.

Готуємось до індивідуального опрацювання

Знайди площу прямокутного трикутника, катети якого дорівнюють 12см і 9см.
Знайди площу прямокутного трикутника, катети якого дорівнюють 6см і 5см.
Діагоналі ромба дорівнюють 12см і 7см. Обчисли його площу.
Знайди число сторін опуклого многокутника, сума кутів якого .
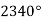Площа трапеції дорівнює 168см², одна з її основ – 20см, а висота – 12см. Знайди другу основу трапеції.
Знайди площу прямокутного трикутника, якщо висота, проведена до гіпотенузи, поділяє її на відрізки завдовжки 2см і 8см.

Урок №8

«Загублений той час,

який ти не використав на навчання»

Пліній, історик Стародавнього Риму

Внутрішньопредметне узагальнення матеріалу

Многокутники. Площі многокутників

І. Систематизація та узагальнення теоретичних знань

Завдання 1.

Повтори блок № 6.
Дай письмово відповідь на питання, запропоновані вчителем.

ІІ. Систематизація та узагальнення практичних умінь та навичок

Завдання 2.

Усно розв’яжи вправи:

Яке з наведених тверджень неправильне?

Многокутник опуклий, якщо всі його кути менші від розгорнутого

Рівні фігури мають рівні площі

Сума кутів опуклого n-кутника дорівнює

180° (n – 2)

Площа ромба дорівнює добутку його діагоналей

Обчисли площу прямокутника зі сторонами 4 см і 5 см.

А	Б	В	Г
9 см²	18 см²	20 см²	20 см

Чому дорівнює сума внутрішніх кутів опуклого чотирикутника?

А	Б	В	Г
360°	540°	720°	1080°

Завдання 3.

Письмово виконай вправи:

Обчисли площу трапеції з основами 10 см і 14 см та висотою 5 см.
Знайди периметр квадрата, якщо його площа дорівнює 49 см².
Знайди гіпотенузу прямокутного трикутника, якщо його площа дорівнює 40 см², а висота, проведена з вершини прямого кута, 5 см.
Один з кутів опуклого п’ятикутника дорівнює 115°, другий, третій і четвертий відносяться як 6 : 5 : 1, а п’ятий дорівнює різниці другого і четвертого кутів. Знайди невідомі кути п’ятикутника.
Знайди площу прямокутного трикутника, якщо висота, проведена до гіпотенузи, поділяє її на відрізки завдовжки 4 см і 9 см.
Сторони паралелограма дорівнюють 16 см і 20 см, а одна з висот – 12 см. Знайди другу висоту паралелограма. Скільки розв’язків має задача?

Тема №7. Повторення матеріалу, вивченого протягом року

Урок №1

«…принципи геометрії є принципами всієї математики»

Омар Хайям

Внутрішньопредметне узагальнення за рік

Завдання 1.

Усно виконати вправи:

Знайдіть площу квадрата зі стороною 8 см.

А	Б	В	Г
16	64	32

Обчисліть середню лінію трапеції, основи якої дорівнюють 2 см і 8 см.

А	Б	В	Г
16 см	10 см	5 см	м

У прямокутному трикутнику АВС 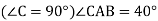, АС = 7 см. А Знайдіть: 1) ВС; 2) АВ.

В С

Завдання 2.

Письмово виконати вправи:

Один з кутів паралелограма на 32° більший від іншого. Знайдіть кути паралелограма.
Діагоналі ромба дорівнюють 24 см і 32 см. Обчисліть периметр цього ромба.
Сторони трикутника дорівнюють 2 см, 8 см і 9 см. Чому дорівнюють сторони подібного трикутника, периметр якого 38 см?
У рівнобічній трапеції основи дорівнюють 14 см і 30 см, бічна сторона – 10 см. Знайдіть площу трапеції.

docx

Завантажити

Зберегти на потім

Додав(-ла)

Суворова Олеся Миколаївна

Пов’язані теми

Геометрія, 8 клас, Матеріали до уроків

Додано

22 січня 2020

Переглядів

22162

Оцінка розробки

Відгуки відсутні