Посібник.Творчі завдання з геометрії для 8 класу
В даному посібнику представлені пошукові завдання для розвитку креативного мислення на уроках геометрії в 8 класі. Технологія розвитку креативного мислення дає можливість в процесі навчання спонукати дитину до дослідницької творчої активності, створювати умови для усвідомлення ними матеріалу, узагальнення одержаних знань для того, щоб навчити дитину підходити творчо до підготовки уроків і систематично стимулювати креативне мислення учнів.
Пропоновані завдання допомагають вчителеві математики розвивати креативне мислення на уроках геометрії та спонукають учнів творчо підходити до розв'язування завдань.


Талант і творча обдарованість особистості стають сьогодні запорукою інтенсивного економічного розвитку країни і сприятливим фактором національного престижу.
Вихід із становища, яке склалося сьогодні, слід шукати у глибокій рівневій і профільній диференціації математичної підготовки, розробці й використанні нових технологій навчання і сучасних інформаційних технологій. Вони мають забезпечити не лише озброєння учнів системою математичних знань і умінь, а і формування в процесі навчання творчої особистості школярів.
Щоб формувати творчу особистість у процесі навчання математики сьогодні, кожен вчитель повинен бути обізнаним із сутністю творчого процесу, сучасним уявленням про нього, методами вивчення творчості, якостями творчої особистості та їх системою, щоб мати змогу формувати такі якості у школярів. Кожний вчитель має вміти діагностувати рівень творчості, знати основні форми, шляхи і механізми формування творчої особистості, зокрема головний з них – творчу задачу.
Школа покликана виявити якості творчої особистості в учнів, і розвивати їх у всіх школярів, зважаючи, звичайно, на те, що діти народжуються з різними задатками творчості. Водночас більшою мірою потрібно дбати про розвиток творчої особистості у здібних та обдарованих учнів.
«Творча особистість – це людина, здатна проникати в суть ідей і втілювати їх усупереч усім перешкодам аж до отримання практичного результату. Саме це мав на увазі Т. Едісон, коли казав, що винахід – це 10% натхнення і 90% поту».
Колись великий Ейнштейн висловив цікаву думку: «Відкриття неможливо зробити, якщо дотримуватися абсолютної логіки». Що ж потрібно хоча б для маленького відкриття? Відповідь проста – потрібно мислити творчо, мати добре розвинуті творчі здібності.
А що таке творчі здібності? Німецький психолог Фромм казав, що творчість – «це здатність дивувати і пізнавати, вміння знаходити рішення в нестандартних ситуаціях».
На уроках математики я виділяю такі основні властивості творчої особистості:
- сміливість думки, схильність до ризику;
- фантазія;
- уявлення і уява;
- проблемне бачення;
- вміння долати інерцію мислення;
- здатність виявити суперечності;
- вміння переносити знання і досвід у новій ситуації;
- незалежність;
- альтернативність;
- гнучкість мислення;
- здатність до самоуправління.
Одним із основних моїх завдань є формування творчої особистості, але у класі не всі діти мають однакові здібності, а я, як вчитель, повинна розвивати їх у кожного учня і на кожному уроці. Для цього використовую систему вправ, які будуть сприяти розвитку креативного мислення учнів.
Запропоновані мною завдання повинні відповідати умовам:
- Мати багато розв’язків.
- При розв’язанні застосовувати інформацію, отриману в одному контексті для виконання в іншому.
- Розвивати нешаблонність мислення.
Разом з вчителями інформатики я складаю різні типи навчальних програм:
- демонстраційні;
- контролюючи;
- програми-тренажери.
Працюючи у звичайних класах, де кількість годин зменшена, я зустрічалася з певними проблемами, перш за все пов'язаними з тим, що для ґрунтовного вивчення математики просто не вистачає часу. Тому замислилася, як раціонально спланувати час на уроці, щоб достатню увагу приділити всім учням, враховуючи особливості та здібності кожної дитини. Але раціональне використання часу вивільняло ще 5—8 хвилин, чого було не достатньо.
Потрібен інший підхід. Я спробувала поділити клас на 3 групи (ряди). Причому поділ на групи може бути різний, залежно від того, якої мети ви хочете досягти на уроці. Діти можуть бути поділені на нерівносильні групи, що
відрізняються швидкістю сприйняття навчального матеріалу. Такий поділ доцільно використовувати на уроках, метою яких є навчити кожного виконувати певні логічні кроки або розв'язувати певні завдання та вправи, наприклад, під час вивчення тем: «Додавання і віднімання многочленів», «Множення многочлена на одночлен», «Множення многочленів», «Формули скороченого множення», «Числові нерівності та їх властивості», «Розв'язування нерівностей з однієї змінною», «Квадратні нерівності» та інших, де завдання не дуже об'ємні, не потребують багато часу для обґрунтування та розв'язання.
На початку уроку кожен ряд одержує диференційоване завдання, і діти працюють не цілим класом, а певною групою, їм виділена третина дошки, і вони мають свій варіант класної, а згодом і домашньої роботи. На такому уроці є можливість опитати втричі більше учнів. За правильністю виконання завдань слідкують самі учні під ненав'язливим та непомітним контролем учителя.
Якщо певна група не в змозі розв'язати проблему, що виникла, то залучається «сильний» учень з іншої групи. Якщо завдання об'ємне, то група, зібравшись разом, обговорює послідовність виконання, розбиває на кроки, над кожним з яких працює окремий учень. Це дало можливість запропонувати учням 7-го класу під час вивчення теми «Рівняння» розв'язати рівняння:
![]()
![]()
Або під час вивчення «Відношення та пропорції» більш ретельно вивчити задачі на пропорційний поділ величин, що сприяло легшому розумінню при розв'язування геометричних задач аналогічно змісту з тем: «Основні геометрич-
ні фігури та їх властивості», «Суміжні та вертикальні кути», «Рівнобедрений трикутник», «Сума кутів трикутника» та ін., показати учням наступність та логічний зв'язок між алгеброю та геометрією як складовими частинами математики. Такий прийом можна використовувати і під час вивчення тем: «Перетворення раціональних виразів», «Арифметична та геометрична прогресії». На таких уроках учні мають можливість працювати і в групі (тобто мати колективну думку), і в парах (де сильніший допомагає слабшому), показати свою індивідуальність.
На уроках, метою яких є узагальнення і систематизація знань з вивченої теми, ділю дітей на рівносильні групи, в які входять як слабші, так і сильніші учні. Але тоді завдання підбираються від простого до складного, щоб слабший учень не відчував себе дискомфортно, а сильний показав свою ґрунтовну підготовку з теми. Як елемент уроку використовую роботу в парах або пропоную для розв'язання проблемні завдання для цілої групи учнів. На таких уроках сильніший учень навчає слабшого непомітно, але результативно.
Такий підхід дає можливість перевірити знання теоретичного матеріалу з геометрії у всіх учнів за короткий час. Причому запитання ставлять учні іншої групи, і кожен зацікавлений в тому, щоб як задати вдале запитання, так і правильно відповісти на поставлене. На таких уроках можна оцінювати запитання, відповіді або розв'язані завдання певною кількістю балів, і урок пройде у вигляді веселого змагання, що покращує емоційний стан учнів, сприяє психологічному розвантаженню, спонукає до кращої підготовки до уроку, згуртовує класний колектив, а найголовніше - розвиває логіку, мислення, знання і вміння, що є базою для вивчення інших предметів шкільного курсу. Оцінювання пропоную проводити учням. Група оцінює кожного учня, аргументуючи виставлений бал. Інколи групи не одразу можуть справедливо виставити бал, тому за такого оцінювання вчитель повинен корегувати цей процес і стежити за тим, щоб до кожної дитини було об'єктивне і доброзичливе ставлення.
За такого ж поділу класу на рівносильні групи під час уроків, метою яких є пояснення нового матеріалу, використовую такий прийом, як «учень-вчитель», де здібний учень пояснює частину нового матеріалу своїм однокласникам. 3 цим учнем проводжу попередню роботу, пояснюю йому основні і важливі моменти теми, що починає вивчатися, на які потрібно акцентувати увагу та виділити особливо чітко. Така практика спонукає здібних учнів до активної пізнавальної та пошукової роботи і розвиває інтерес як до предмета математики, так і до професії вчителя.
Але така диференціація вимагає більше часу на підготовку вчителя до уроку. Варіант класної роботи одного ряду може бути одночасно й варіантом домашньої роботи і для іншого. Тим учням, які мають здібності та виявляють інтерес до вивчення предмета, крім домашнього завдання, що є обов'язковим для всіх, пропонується ще й індивідуальна робота або окреме завдання. Такі учні допомагають у підготовці проблемних запитань та завдань для класу, відшукують цікаві задачі, історичні факти. Такий підхід сприяє підготовці здібних дітей до участі у шкільних та міських олімпіадах з математики.
Все це загалом дає можливість гуманізувати навчально-виховний процес, розвинути творчі здібності учнів, допомагає кожній дитині відчути власну гідність, повірити у свої сили.
Наведу приклади завдань, які сприятимуть розвитку креативного мислення на уроках алгебри.
Алгебра. 7клас.
Тема: Вирази із степенями. Властивості степенів. Одночлен.
Завдання 1.
Після спрощення виразу із степенями, з використанням властивостей степеня, одержали результат: …=а6 в8 с2
Наведіть якомога більше можливих виразів.
На виконання завдання у класі учням потрібно дати 5 хвилин.
Учні можуть навести вирази:
1 учень:
а2в2с ∙ а4в6с = а6 в8 с2;
а в4с2 ∙ а5в4 = а6 в8 с2.
Таких прикладів може бути багато, але вони свідчать, що у учня не розвинута гнучкість і оригінальність мислення.
2 учень:
2а2в3с2∙![]() ;
;
- 0,2а6 в с ∙ (-5) в7 с = а6 в8 с2;
100 ∙ (0,1 а3в4с)2 = а6 в8 с2;
![]() .
.
В учня розвинуті і гнучкість, і оригінальність мислення.
Завдання 2.
Скласти одночлени з коефіцієнтом в, де −4,7 < в < 2, і найбільшим показником степеня, який дорівнює 6.
Примітка: при виконанні цього завдання можна відпрацьовувати властивості степенів, поняття одночлена нестандартного вигляду.
Завдання 3.
При множинні одночленів було отримано:
а) (…) ∙ (…) = 24а2в4с8;
б) (…)∙ (…) = −15(а5в2)2с3.
Записати декілька прикладів, які задовольняють надану умову.
Тема: Многочлен.
Завдання 1.
Записати многочлени, які мають не менше 5 подібних доданків, степень яких не вище за 6.
Привести його до стандартного вигляду.
Завдання 2.
Сума многочленів дорівнює:
а) 5х2 − 2х + 3;
б) − 0,6 а3 + 5в − 4с + 7.
Записати декілька прикладів, які задовольняють надану умову.
Завдання 3.
Що спільного у виразах:
а) −12а2в : 24а4в2с−2а2вс2;
б) 50а5 + 30аd + 50а4в + 30в2 і 25а5в + 15ав2 + 30а + 30в.
Тема: Формули скороченого множення.
Завдання 1.
Які формули скороченого множення ви бачите у виразах?
а) (а2 + в2 + 2ав)(а + в)(а - в)2;
б) (а3 + 3а2в + 3ав2)∙(а−в)(а + в).
Завдання 2.
Розкласти на множники різними способами вираз:
2ах + сх − 6ах2 − 3сх2 + 2ас + с2
Завдання 3.
Продовжити ряд:
2а; 4а2в; 8а3в2; …
а (а + в); а4(а + в)2; а7(а + в)3; …
а − в; а3 − в3; (а3 − в3)(а2 + ав + в2); …
а − в; а2 − в2; (а − в) (а2 + 2ав + в2); … .
Скласти подібні ряди, застосовуючи формули скороченого множення.
Алгебра. 8клас.
Тема: Дрібно-раціональні вирази та їх перетворення.
Завдання 1.
При скороченні дробу було одержано:
а)![]() ;
;
б) ![]()
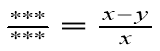 .
.
Запишіть декілька варіантів можливого прикладу.
Завдання 2.
Скласти і розв‘язати декілька прикладів, які задовольняють умову:
![]()
Тема: Квадратні рівняння (теорема Вієтта).
Завдання 1.
Знайти декілька значень параметра а, якщо корені рівняння – цілі числа:
а) х2 − 7х + а = 0;
б) х2 + 9х + а = 0.
Завдання 2.
Знайти суму цілих коренів рівняння:
а) ![]() ;
;
б) ![]() .
.
Отже, із словами Пуассона можна погодитися, або ж ні, але він сказав « У житті немає нічого кращого, як вивчати й викладати математику».


про публікацію авторської розробки
Додати розробку
