Тематична розробка "Подібність трикутників"

 

 

ПОДІБНІСТЬ ТРИКУТНИКІВ

 

ТЕМАТИЧНА РОЗРОБКА

 

 

 

КАЛЕНДАРНЕ ПЛАНУВАННЯ ТЕМИ

 

 

Подібність трикутників	14
Узагальнена теорема Фалеса	1
Подібність трикутників	1
Перша ознака подібності трикутників	1
Друга ознака подібності трикутників.	1
Розв'язування задач. Самостійна робота	1
Третя ознака подібності трикутників	1
Ознаки подібності прямокутних трикутників	1
Властивості подібних  трикутників. Сам.   робота	1
Пропорційні відрізки у прямокутному трикутник	1
Висота, опущена з вершини прямого кута	1
Теорема Піфагора	1
Властивості бісектриси  трикутника	1
Розв'язування задач і вправ. Самостійна робота	1
Контрольна робота	1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ПОДІБНІСТЬ ТРИКУТНИКІВ

 

СИСТЕМА ПРАКТИЧНИХ РОБІТ

 

 

 

Практична робота №1.

 

1. Накресліть гострий кут з вершиною в точці А.
2. Наодній із сторін кута відкладіть від вершини послідовно відрізки АВ=2 см, ВС= 4 см.
3. За допомогою косинця і лінійки через нінці променів проведіть паралельні прямі так, щоб вони перетнули сторону кута в точках В₁ і С₁
4. Виміряйте лінійкою відрізки АВ₁, АС₁, В₁С₁, ВВ₁, СС₁.
5. Порівняйте відношення   а) 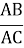, ,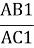 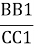; б)  і .
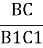6. Зробіть висновки.

 

 

 

Практична робота №2.

 

1.Виріжте з паперу чотири рівних трикутники.

2.Один з них залиште без змін, а від інших відріжте частини, що    відтинаються прямими, паралельними кожній з сторін.

 

 

 

 

 

 

 

 

 

 

 

 

3.Порівняйте кути трьох отриманих трикутників з кутами першого трикутника. Зробіть висновки.

4.Виміряйте довжини сторін  двох утворених трикутників. Порівняйте відношення   довжин їх відповідних сторін. Зробіть висновки.

 

 

 

 

Практична робота №3.

 

1.Побудуйте два рівні кути В і В_1.

2.На  сторонах кутів В і В₁ відкладіть відрізки ВА, ВС, В₁А₁, В₁С₁    відповідно так, щоб В₁А₁=1,5 ВА, В₁С₁=1,5 ВС.

3.Сполучіть точки А і С, А₁ і С₁. Виміряйте  відрізки  АС і А₁С_1.

 4.Обчисліть відношення А₁С₁ : АС та виміряйте кути ВАС і В₁А₁С₁. Зробіть висновки.

 

Практична робота №4.

1.                                                                                                                                                                                                           Накресліть два відрізки АВ, А₁В₁, так, щоб АВ=2 А₁В₁  і два гострі кути α і β.
2.                                                                                                                                                                                                           Побудуйте трикутники АВС і А₁В₁С₁  за двома кутами ( ∠А=∠А₁= α;

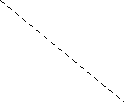
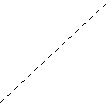∠В=∠В₁= β) і стороною відповідно АВ і А₁В₁.

         

      С

С₁

 

А                                                               В₁     А₁            В₁

3.     Виміряйте лінійкою відрізки АС, А₁С₁, ВС, В₁С₁.

4.Обчисліть відношення   = . Зробіть висновок.

 

Практична робота №5.

 

1. Побудуйте трикутники АВС і А₁В₁С₁  затрьома сторонами так, щоб

     АВ=2,5 А₁В₁ ,  ВС =2,5 В₁С₁,АС= 2,5А₁С₁.

2.Виміряйте кути трикутників АВС і А₁В₁С₁. Зробіть висновки.

 

 

Практична робота №6.

 

1.Накресліть прямокутний трикутник.

2.З довільної точки гіпотенузи трикутника проведіть перпендикуляри до  його катетів.

3.Виміряйте довжини сторін утворених трикутників і порівняйте їх із довжинами сторін  заданого вами трикутника. Зробіть висновки.

4.З довільної точки одного з катетів  заданого трикутника проведіть перпендикуляр до його гіпотенузи. Виміряйте дрвжини сторін утворених трикутників і порівняйте їх з довжинами сторін заданого вами трикутника. Зробіть висновки.

 

 

Практична робота №7.

1.Накресліть гострокутний трикутник  АВС. Побудуйте його бісектрису ВL, висоти АН і ВК та медіану СМ та виміряйте їх довжини.

2.Побудуйте трикутник  А₁В₁С₁  , подібний до трикутника АВС. Як ви це зробили? За якою ознакою подібні ваші трикутники? Знайдіть коефіцієнт подібності цих трикутників.

3.Побудуйте  у трикутнику А₁В₁С₁  бісектрису В₁L₁, висоти А₁Н₁ і В₁К₁ та медіану С₁М₁  та виміряйте їх довжини.

4.Знайдіть відношення відповідних бісектрис, висот і медіан подібних трикутників АВС і  А₁В₁С_1. Порівняйте значення отриманих відношень з коефіцієнтом подібності трикутників. Зробіть висновок.

5.Накресліть тупокутний трикутник і подібний до нього. Проведіть у цих трикутниках відповідні висоти і виконайте практичну роботу, аналогічну пунктам 3,4.

 

Практична робота №8.

 

1.Побудуйте трикутник  АВС .Визначте положення центрів його описа-ного і вписаного кіл. Як ви це зробили?

2. Побудуйте трикутник А₁В₁С_{1 ,} подібний до трикутника АВС. За якою ознакою подібні ваші трикутники? Визначте їх коефіцієнт подібності.

3. Визначте положення ценрів  описаного і вписаного кіл ∆А₁В₁С₁.

4. Знайдіть довжини радіусів описаного і вписаного кіл трикутників. Як ви це зробили?

5. Обчисліть відношення   радіусів відповідних кіл подібних  ∆АВС і ∆А₁В₁С₁. Порівняйте їх зі значенням  коефіцієнта подібності. Зробіть висновок.

Практична робота №9.

 

1. Побудуйте  ∆ АВС  . Проведіть його середні лінії.
2. Побудуйте ∆А₁В₁С₁, сторонами якого є відрізки, довжини яких дорівнюють середнім лініям трикутника АВС.З'ясуйте, чи подібні ці трикутники. Як ви це зробили?
3. Якщо ваші трикутники подібні, визначте їх коефіцієнт подібності.
4. Проведіть прямі через вершини ∆АВС, паралельно їх протилежним сторонам. Точки перетину цих прямих позначте як А₂В₂С₂.

5.З'ясуйте, чи подібні ці трикутники. Як ви це зробили?

      6. Якщо ваші трикутники подібні, визначте їх коефіцієнт подібності.

7. З'ясуйте, чи подібні ∆ А₁В₁С₁ та ∆ А₂В₂С₂. Як ви це встановили?

      8. Якщо ці трикутники подібні, визначте їх коефіцієнт подібності.

9.Знайдіть довжини радіусів кіл,описаних навколо цих трикутників.-Обчисліть їх відношення.Порівняйте значення відношення з зі значенням  коефіцієнта подібності

 

ПОДІБНІСТЬ ТРИКУТНИКІВ

СИСТЕМА УСНИХ ВПРАВ.

До уроку " Узагальнена теорема Фалеса "

1.Розв'язати пропорцію , 4:0,2х=8:4.

2.Записати відношення відрізків , якщо прямі k i l паралельні (зробити відповідні позначення)

 

     k l  A   

 

          

 

 

 

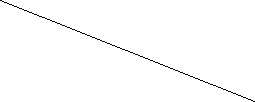
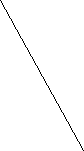
B 

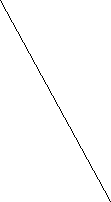
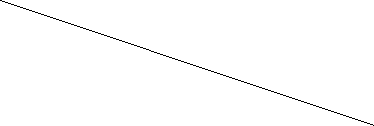
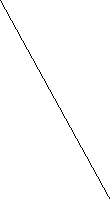3.Записати відношення відрізків OF:FG:GH, якщо  ОА=5см,АВ=4см, ВС=3см.             

 

     C

 

O   A       В        

 

            F   G  

      H

До уроку "  Подібність трикутників "

1. Гомотетія з центром О(0;0) переводить точку А(-1;-2) в точку А'(- ;- 1) Який коефіцієнт гомотетії?
2.  ∆МНР∆КВС. Що звідси випливає?
3. Чи подібні трикутники на малюнку? Якщо так, то назвіть відповідні сторони і кути.                                          F

      M

                

      А    D N    L

 

До уроку " Перша ознака подібності трикутників "

1. Відомо,що ∆АВС ∆КМР.Назвіть відповідно рівні кути цих трикутників.
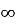
2. ∆АВС   і трикутник з вершинами  D,E,F подібні, причому

  = = .Закінчіть запис: ∆АВС∆… .

3.Чи рівні будь-які два подібні трикутники? Чи подібні  будь-які два рівні трикутники? Назвіть відповідний коефіцієнт подібності.

4.Чи можуть бути подібними прямокутний і тупокутний трикутники?

5.Два трикутники подібні з коефіцієнтом 0,25. У скільки разів сторони одного  трикутника більші  за відповідні сторони іншого?

 

До уроку " Друга ознака подібності трикутників "

1.Трикутниках АВС  і  А₁В₁С₁  =k. Яку рівність необхідно додати до умови, щоб можна було довести подібність  цих трикутників? Назвіть усі можливі варіанти відповіді.

2.Дано ∆АВС і ∆КМN = = . Назвіть кут ∆KMN  , що дорівнює ∠С. Чому ці кути рівні?

3. Дано  трикутники ABC і  KMN, в яких   =  ∠B=∠N. Назвіть кут  ∆АВС,що дорівнює куту   M.Чому ці кути рівні?

 

До уроку " Третя ознака подібності трикутників "

1. Чи можуть бути подібними :

1. Прямокутний і рівносторонній трикутники?
2. Трикутник із кутом 50° і трикутник із кутом 100°?
3. Трикутник  із кутом 60° і трикутник із кутом 120°?

2.Чи подібні рівнобедрені трикутники, якщо вони мають:

1. По рівному гострому куту?
2. По рівному тупому куту?

3.Два подібні  трикутники мають спільний кут. Чи обов'язково їх сторони, протилежні цьому куту, паралельні? Наведіть контрприклид.

4. ∆АВС ∆ КМР з коефіцієнтом подібності 0,5.АВ= 5 см, ВС=7см,

АС= 8см. Назвіть величину сторін  ∆КМР.

 

 

До уроку " Ознаки подібності прямокутних трикутників "

1. Чи подібні два прямокутні трикутники, якщо:

1. вони мають спільний кут?
2. вони мають спільний  гострий  кут?
3. один  із них має кут 20° а інший – кут 70°?
4. один  із них має кут 50°, а катет другого вдвічі менший за гіпотенузу?

2. Чи подібні трикутники на малюнку? Hазвіть відповідні елементи.

   24  40   60  

            36        48

   32

 

До уроку " Властивості подібних  трикутників"

1.Дано два прямокутні рівнобедрені трикутники. Чи можна стверджувати, що вони подібні?

2.На малюнку знайдіть пари подібних трикутників. Свої міркування обгрунтуйте.Запишіть пропорційність відповідних сторін.

    C           B          A

         K

                H

     B

A       F

      A  M  F C  M      B

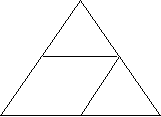C            K

          

E    D

A D  B         F     B       P         

 A

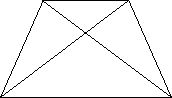          E B      N

      C            

     A   B D      A       S

 

 

 

 

 

 

До уроку " Висота, опущена з вершини прямого кута"

1.Чи може висота прямокутного трикутника, проведена до гіпотенузи,

                      а)бути меншою за кожну з проекцій катетів на гіпотенузу;

б) дорівнювати проекції катета на гіпотенузу;

в)дорівнювати катету?

2.Відрізки а_с  і b_с – проекції катетів а і b прямокутного трикутника на гіпотенузу.Порівняйте:

1. а і b, якщо а_с  < b_с;
2. а_с  і b_с , якщо а b.

3. Чи можуть бути подібними нерівні прямокутні трикутники:

1. зі спільною гіпотенузою;
2. зі спільним катетом?

 

До уроку " Теорема Піфагора"

1. Квадрат гіпотенузи прямокутного трикутника вдвічі більший за квадрат катета. Чому дорівнюють готрі кути трикутника?
2. Яку градусну міру має  найбільший  кут трикутника зі  сторонами 6см , 8 см, 10см? Чому?
3. Сторони паралелограма дорівнюють  3см і 4 см, а діагональ ­-   5см. Визначити вид паралелограма.
4. У трикутнику  АВС  ∠А =90°. Назвіть:

1. похилу до прямої АВ, проведену з точки С;
2. проекцію похилої  ВС на пряму  АС.

5. Відрізки  а₁ і  а₂  -  проекції похилих  l₁  та   l₂ , проведених з однієї точки до однієї прямої. Порівняйте :

1. l₁  і   l₂ , якщо а₁  < а₂ ;
2. а₁  і а₂,  якщо l₁  =   l₂.

6.Дві похилі до однієї прямої мають рівні проекції. Чи обов'язково ці похилі рівні?

7.Скільки  рівних похилих до даної прямої можна провести з точки, яка не лежить на цій               прямій?

 

До уроку " Властивості бісектриси  трикутника"

 1.Бісектриса трикутника ділить протилежну сторону увідношенні 1:2. Чи можуть кути, прилеглі до цієї сторони, бути рівними? Чому?

2.Чи може бісектриса рівнобедреного трикутника ділити бічну cторону у відношенні 2:1, починаючи від основи? Якій теоремі це суперечить?

 

Подібність трикутників

Контрольна робота

Варіант 1

 

1°.У прямокутному  трикутнику гіпотенуза дорівнює 13см, а один з катерів ─ 12 см. Знайти периметр трикутника.

 

2°.З однієї точки до даної прямої проведено дві рівні похилі. Відстань між їх основами дорівнює 28  см. Визначити довжини проекцій похилих на дану пряму.

 

3˙. Висота ВМ рівнобедреного трикутника АВС (АВ =АС)  ділить сторону АС на відрізки АМ= 15 см і СМ= 2 см.  Знайти основу ВС трикутника.

 

4˙. З точки до прямої проведено дві похилі, проекції яких на пряму дорівнюють 9 см і 16 см. Знайти відстань від точки до прямої, якщо одна з похилих на 5 см більша за другу.

 

5˙˙. Довести, що сума діагоналей трапеції більша за суму її бічних сторін.

Варіант 2

 

1°. У прямокутному трикутнику  катети дорівнюють 8 см і 15 см. Знайти периметр трикутника.

 

2°. З однієї точки до даної прямої проведено дві рівні похилі. знайти відстань між основами похилих, якщо проекція однієї з них дорівнює 16 см.

 

3˙.Висота АК гострокутного рівнобедреного трикутника  АВС (АВ=ВС) дорівнює 12 см, а КВ= 9 см. Знайти сторони трикутника АВС.

 

4˙. З точки до прямої проведено дві похилі, довжини яких  дорівнюють 13 см   і 15 см. Знайти відстань від точки до прямої, якщо різниця проекцій похилих дорівнює 4 см..

 

5˙˙. Довести, що сума діагоналей трапеції більша за суму її основ.

 

Використана література

1. Апостолова Г.В., Геометрія 8 клас – Київ, «Генеза», 2008
2. Єршова А.П.,Голобородько В.В.,Крижановський О.Ф,

 Єршов С.В. Геометрія 8 клас – Харків, АН ГРО ПЛЮС, 2008;