Позакласна робота з математики у 7-9 класах
Позакласна робота
з математики у 7 – 9 класах
ПЛАН
Вступ
- Зміст та принципи позакласної роботи……………………………………..…5
-
Напрямки позакласної роботи з математики…………………………….…...6
- Роль позакласної роботи в підготовці учнів, що відстають від інших
у вивченні програмного матеріалу……………………………………….…..7
- Роль позакласної роботи в підготовці учнів, що виявляють
до математики підвищену цікавість і здібності………………………………9
3. Форми організації позакласної роботи з математики………………………….10
3.1 Роль гурткової роботи у підвищенні інтересу учнів до математики....11
3.2 Математичні вечори ………………………………………………...…..18
3.3 Математичні вікторини……………………………………….………....22
3.4 Математичні турніри й естафети…………………………….……….....24 3.5 Математичні олімпіади……………………………………………..…....27
3.6 Математичні екскурсії…………………………………………….….….30
Висновки
ВСТУП
Одним з пріоритетних завдань сучасної школи є створення необхідних і повноцінних умов для індивідуального розвитку кожної дитини, формування активної позиції учнів в навчальному процесі. Тому використання активних форм навчання є основою розвитку пізнавальної компетентності школяра. Активні пізнавальні здібності формуються і розвиваються в процесі пізнавальної діяльності. Коли дитина не просто слухач, а активний учасник в пізнавальному процесі, своєю працею здобуває знання. Ці знання міцніші, ніж ті, що подаються в готовому вигляді. Саме форма активного навчання — це перша іскорка, що запалює факел допитливості. Вчитель відмовляється від авторитарного характеру навчання на користь демократичного пошуково-творчого. Відчуття свободи вибору робить навчання свідомим, продуктивним і результативнішим.
Однією з форм навчально-виховного процесу, що становить частину виховання, є позакласна робота. Правильно поставлена позакласна робота в школі має велике освітнє і виховне значення. Вона розширює і заглиблює знання, отримані на уроці, дозволяє набути багато корисних навичок, а, отже, наближає навчання і виховання до життя. Позаурочна робота полегшує індивідуальний підхід до учнів, створює сприятливі умови для розвитку у них самостійності.
Під час уроків неможливо задовольнити всі питання учнів. Позаурочна робота у взаємозв’язку з урочною служить тим дієвим засобом, який мобілізує активність учня в пошуку знань і допомагає повніше задовольнити інтереси школярів.
Незважаючи на різноманітність форм навчальної діяльності позакласна робота з математики повинна бути органічно пов'язана з шкільною програмою, виходити за межі і разом з тим доповнювати її, тобто повинен існувати тісний взаємозв'язок між урочною і позаурочною роботою.
Мета курсової роботи — розкрити методику проведення позакласної роботи з математики у 7-9 класах загальноосвітньої школи.
Об’єктом дослідження є процес вивчення математики в загальноосвітній середній школі.
Предметом дослідження є форми організації позакласної роботи з математики в 7-9 класах.
Для виконання поставлених завдань використовувалися такі методи дослідження:
- аналіз психолого-педагогічної та методичної культури із зазначеної проблеми;
- аналіз програм, навчальних посібників, підручників з математики;
- вивчення досвіду вчителів I-II рівня;
- спостереження, бесіди.
1. Зміст та принципи позакласної роботи
У педагогічній енциклопедії “позакласна робота” визначається як ”складова частина навчально-виховного процесу в школі, одна з форм організації вільного часу учнів”.
Позакласна робота з предмету відіграє величезну роль для сучасної школи. В умовах перебудови соціального і економічного життя суспільства сильно зростає роль позакласної роботи у вихованні нової особистості. Ця робота робить внесок до таких якостей особи, як ініціативності, активності, творчості, здібності до саморозвитку, самовиховання, самоосвіти. Позакласна робота — це, з одного боку, педагогічна система, що володіє цілісними властивостями і закономірностями функціонування, а з іншої - невід'ємна частина вітчизняної системи освіти. З цієї причини однією з центральних проблем методики позакласної роботи завжди була проблема взаємозв'язку урочних і позаурочних занять як окремий випадок фундаментальної педагогічної проблеми цілісності навчально-виховного процесу.
Принципи позакласної роботи:
– добровільності (принцип, що враховує бажання школярів взяти участь в позакласній роботі);
– обліку індивідуальних особливостей учнів (принцип обліку відмінності спрямованості інтересів і рис характеру учнів);
– комунікативної активності (принцип, що стимулює і залучає учнів до використання нових, невідомих ними матеріалів, пізнавальна цінність і цікавість яких викликають потребу в спілкуванні, підвищують їх якісний рівень, що сприяє розвитку комунікативної компетентності школярів).
Як і в навчанні будь-якому шкільному предмету, в позакласній роботі з математики зміст відбирається довільно. Тематика позакласної роботи дуже різноманітна. У позакласній роботі більше, ніж в будь-якій іншій діяльності педагога, виявляється вплив особи вчителя, його кругозору, інтересів, теоретичного і етичного багажу.
Вимоги до змісту позакласної роботи :
- науковості (встановлює певне співвідношення змісту шкільного предмету із змістом науки);
- доступності (зміст повинен відповідати віковим особливостям учнів, не йти далеко від шкільної програми, стимулювати прагнення до пізнання, до роботи з додатковою літературою, до дослідницької діяльності);
- актуальності і практичної значущості (зв'язок з життям);
- цікавості (учням повинно бути цікаво під час проведення позакласної роботи).
2. Напрямки позакласної роботи з математики
Особливістю організації навчально-виховного процесу в сучасних умовах є орієнтація на досягнення всіма учнями обов'язкового рівня математичної підготовки і створення умов для навчання на більш високому рівні для тих учнів, хто має здібності, інтерес до математики. У зв'язку з цим особливу увагу треба приділяти диференційованому навчанню та індивідуальній роботі з учнями не тільки на уроках, а й у позаурочний час.
Вимоги, що передбачені програмою з математики, шкільними підручниками і методикою навчання розраховані на так званого “середнього” учня. Проте вже з перших класів починається різке розшарування колективу учнів: на тих, хто легко і з цікавістю засвоюють програмний матеріал з математики, на тих, хто добивається при вивченні математики лише задовільних результатів, і тих, кому успішне вивчення математики дається дуже важко.
Оскільки позакласна робота повинна бути диференційована, спрямована на задоволення інтересів і запитів учнів, а учні проявляють різні здібності та інтереси, то розрізняють два напрямки позакласної роботи з математики:
1) робота з учнями, які не досягли обов'язкового рівня у вивченні програмного матеріалу, або, які бажають підвищити свій рівень навчальних досягнень з певної теми (додаткові позакласні заняття);
2) робота з учнями, що виявили до вивчення математики підвищений інтерес та здібності (це позакласна робота у традиційному розумінні).
2.1. Роль позакласної роботи в підготовці учнів, що відстають від інших у вивченні програмного матеріалу
В ідеальному випадку цей вид позакласної роботи повинен мати яскраво виражений індивідуальний характер і виявлятися лише у виняткових випадках (наприклад, у разі тривалої хвороби учня, переходу з школи іншого типу т. п.). Проте в даний час ця робота вимагає ще значної уваги з боку вчителя математики.
Головна її мета — своєчасна ліквідація (та попередження) прогалин у знаннях, уміннях і навичках учнів з курсу математики.
Роботу з такими учнями найкраще проводити індивідуально, бо прогалини в знаннях учнів різні. Проте можна виділити теми, які важко засвоюються багатьма. За такими темами варто проводити групову роботу.
Завдання для цих учнів повинні бути посильними для них, по можливості, мати практичний характер, викликати інтерес, містити підказки, зразки розв'язань, рисунки.
Досвід роботи вчителів показує, що для розуміння і відтворення розв'язання, учню треба розв'язати майже по 2-3 однакові задачі. Працюючи з учнями, треба пам'ятати, що будь-який бал, що набрала дитина, має розглядатись як позитивний результат.
Новим напрямком у додатковій роботі і не дуже розробленим у методичній літературі, є робота з учнями, що бажають підвищити свій рівень навчальних досягнень, тобто з учнями, які мають 5, 7, 8, 9 балів.
Для досягнення ефективних результатів у роботі із учнями, що хочуть покращити свої знання з математики потрібно дотримуватись наступних положень, пов'язаних з організацією і проведенням позакласної роботи:
1. Додаткові (позакласні) заняття з математики доцільно проводити з невеликими групами учнів (по 3-4 людини в кожній).Ці групи учнів повинні бути достатньо однорідні як з погляду пропусків, що є у школярів, в знаннях, так і з погляду здібностей до навчання. Важливим в цьому плані є поелементний аналіз самостійних і контрольних робіт.
Наведемо схему поелементного аналізу контрольної роботи у 7 класі по темі «Дії з одночленами та многочленами»
|
Елементи знань, умінь |
Кількість учнів |
Прізвище учня |
– суму многочленів – різницю многочленів – добуток многочленів
|
|
|
2. Слід максимально індивідуалізувати ці заняття (наприклад, пропонуючи кожному з таких учнів наперед підготовлене індивідуальне завдання і надаючи в процесі його виконання конкретну допомогу кожному).
3. Заняття з тими, що відстають в школі доцільно проводити не частіше ніж один раз в тиждень, поєднуючи цю форму занять з домашньою роботою учнів по індивідуальному плану.
4. Після повторного вивчення того або іншого розділу математики на додаткових заняттях необхідно провести підсумковий контроль з виставлянням оцінки по темі.
5. Додаткові заняття з математики, як правило, повинні мати повчальний характер; при проведенні занять корисно використовувати відповідні варіанти самостійних або контрольних робіт з "Дидактичних матеріалів", а також навчальні посібники (і завдання) програмованого типу.
6. Вчителеві математики необхідно постійно аналізувати причини відставання окремих учнів при вивченні ними математики, вивчати типові помилки, що допускаються під час вивченні тієї або іншої теми. Це робить додаткові заняття з математики ефективнішими.
2.2. Роль позакласної роботи в підготовці учнів, що виявляють до математики підвищену цікавість і здібності.
Другий з вказаних вище напрямів позакласної роботи з математики заняття з учнями, що виявляють до її вивчення підвищену цікавість, відповідає наступним основним цілям:
1. Пробудження і розвиток стійкого інтересу учнів до математики і її додатків.
2. Розширення і поглиблення знань учнів за програмним матеріалом.
3. Оптимальний розвиток математичних здібностей в учнів і вироблення в учнів певних навиків науково-дослідного характеру.
4. Виховання високої культури математичного мислення.
5. Розвиток в учнів уміння самостійно і творчо працювати з навчальною і науково-популярною літературою.
6. Розширення і поглиблення уявлень учнів про практичне значення математики в техніці і практиці.
7. Розширення і поглиблення уявлень учнів про культурно-історичну цінність математики.
8. Виховання учнів відчуття колективізму і уміння поєднувати індивідуальну роботу з колективною.
9. Встановлення тісніших ділових контактів між вчителем математики і учнем, і на цій основі глибше вивчення пізнавальних інтересів і запитів школярів.
10. Створення активу, здатного надати вчителеві математики допомогу в організації ефективного навчання математиці всього колективу даного класу (допомога у виготовленні наочностей, заняттях з тими, що відстають, в пропаганді математичних знань серед інших учнів).
Передбачається, що реалізація цих цілей частково здійснюється на уроках. Проте в процесі класних занять, обмежених рамками навчального часу і програми, це не вдається зробити з достатньою повнотою. Тому остаточна і повна реалізація цих цілей переноситься на позакласні заняття з математики.
3. Форми організації позакласної роботи з математики.
За способом організації позакласна робота з математики поділяється на масову, групову та індивідуальну. Кожна з них має свої переваги і недоліки. Масова робота дає змогу залучати до неї колектив учнів. У такому масовому вияві творчості легко організувати змагання, проте важко забезпечити глибоке проникнення всіма учасниками в суть пропонованих математичних залежностей, проконтролювати діяльність кожного учасника. Зрозуміло, що важко й підтримувати тривалий час продуктивну роботу великого учнівського колективу.
Більш результативною є робота з невеликою групою, як правило, тих самих учнів, наприклад, членів математичного гуртка. Індивідуальна робота проводиться тут відповідно до інтересів учнів.
Традиційними і найбільш поширеними формами позакласної роботи з математики є:
• математичні гуртки;
• математичні вечори, КВК;
• математичні вікторини;
• математичні турніри;
• математичні естафети;
• математичні стінгазети;
• математичні олімпіади;
• позакласне читання з математики;
• математичні екскурсії.
3.1 Роль гурткової роботи у підвищенні інтересу учнів до математики
Підвищенню інтересу дітей до математики сприяє гурткова робота.
Математичний гурток – одна з найбільш дієвих і ефективних форм позакласних занять. В основі гурткової роботи лежить принцип строгої добровільності. Зазвичай гурткові заняття організовуються для учнів, що мають добру успішність. Проте слід мати на увазі, що іноді учні із поганою успішністю виявляють бажання брати участь в роботі математичного гуртка і нерідко досить старанно виконують всі завдання. Вчителеві математики не слід цьому перешкоджати. Необхідно лише уважніше віднестися до таких учнів, постаратися закріпити інтерес, що є у них, до математики, простежити за тим, щоб робота в математичному гуртку була для них посильною. Звичайно, наявність слабких учнів серед членів математичного гуртка утруднює роботу вчителя, проте шляхом індивідуалізації завдань, які пропонує вчитель, можна в деякій мірі ослабити ці труднощі. Головне зберегти масовий характер гурткових занять з математики, що є наслідком доступності для всіх охочих.
У школах, де є кілька паралельних класів, гуртки можна організовувати окремо для учнів кожного з 5-11 класів. Проте, найчастіше організовують окремі гуртки для учнів 5-6, 7-9, 10-11 класів. У план роботи цих гуртків включають питання, які б були цікаві і доступні для всіх учнів, але в окремих випадках, коли розглядаються питання, пов’язані з програмним матеріалом старших класів, присутність на занятті учнів молодших класів не обов’язкова.
На першому занятті гуртка треба намітити основний зміст роботи, вибрати старосту, домовитися з учнями про права і обов'язки членів гуртка, скласти план роботи і розподілити доручення на ті або інші заходи (випуск математичної стінної газети, ведення документації роботи кружка і т. п.).
Заняття гуртка доцільно проводити двічі на місяць, виділяючи на кожне заняття по одній годині.
Щоб забезпечити явку на перше заняття, бажано розповісти на уроці щось цікаве (епізод з історії математики, софізм, цікаву задачу), а потім запропонувати стати членом гуртка.
На перше заняття прийдуть багато учнів. Проте на друге заняття їх приходить все менше. Тут треба уточнити список і зобов’язати всіх цих бажаючих систематично відвідувати гурток.
Коли склад членів гуртка стабілізувався, корисно уточнити план роботи, враховуючи інтереси гуртківців.
Щоб залучити всіх членів гуртка до активної роботи, бажано створити секції, які займаються:
- збиранням народних задач;
- виготовленням наочних посібників;
- упорядкуванням історичного матеріалу з математики;
- оформленням матеріалів, які характеризують прикладний характер математики;
- випуском математичної стінгазети.[1]
Зміст роботи гуртка охоплює такі напрями: поглиблене вивчення програмного матеріалу, розширення теоретичних відомостей, пов’язаних із методів, законів, формул, що вивчаються; розв’язування олімпіадних задач;
Так, розглядаючи теорему Піфагора у 8 класі, учитель може сформулювати так звану «велику теорему Ферма»: «Якщо показник n – ціле додатне число, більше 2, то неможливо знайти три таких додатних чисел x, y, z, які б задовільняли рівняння ![]() .
.
Вивчаючи у 7 класі тему «Стандартний вигляд числа» можна ознайомити учнів з числами-велетнями та числами-карликами.
Викладаючи у 9 класі матеріал по темі «Елементи прикладної математики» вчитель пропонує учням довести твердження про середні величини в трапеції.
 D b C
D b C
![]() E F
E F
![]()
![]() R S
R S
![]() M N
M N
![]() P O
P O
A B
а
а) Довжина лінії EF, що проходить через точку перетину діагоналей трапеції, є середнім гармонічним чисел a і b:
![]()
б) Довжина лінії RS, що поділяє трапецію на частинки, відношення площ яких дорівнює a:b, буде середнім геометричним чисел a i b:
![]()
в) Довжина відрізка PQ, що поділяє трапецію на рівновеликі трапеції, є середнім квадратичним її основ:
![]()
![]()
До цих властивостей можна звернутись при вивченні у 9 класі теми «Нерівності», встановивши такі співвідношення:
![]()
Матеріали для роздумів під рубрикою”Для допитливих” є у підручнику Г.П.Бевз «Геометрія» 7 клас.[11]
- вивчення відомоcтей з історії математики, ознайомлення з біографіями видатних математиків, розв’язування стародавніх задач.
Вивчаючи іменовані теореми, на уроках вчитель не має змоги, через обмежений час, ознайомити учнів із життям і діяльністю відомих математиків. Але учням цікаво дізнатися наприклад про те, як Фалес Мілетський вразив єгипетських землемірів тим, що визначив висоту піраміди не тільки в тому випадку коли довжина тіні вертикально поставленої віхи дорівнює довжині самої віхи, а й у інших випадках (теорему Фалеса вивчають у 8 класі). З цікавістю слухають учні розповідь про те, що Піфагор брав участь в 58-й олімпіаді з кулачного бою, хоча через малий зріст судді не хотіли допустити його. Для Піфагора ця олімпіада стала спортивним тріумфом, а його вболівальник Фалес – там помер.
Гуртківці не тільки ознайомлюються з подібними історіями з біографії видатних математиків, а й оформляють відповідні альбоми.
Варто приділяти увагу стародавнім історичним задачам.
Задача Ю. Д. Войтяхівського (з підручника «Курс математики», 1787 р.):
«Собака вгледів у 150 сажнях зайця, який перебігає за 2 хв 500 сажнів, а собака за 5 хв 1300 сажнів. Через який час собака дожене зайця?»
- ознайомлення з елементами цікавої математики, зокрема розв’язування математичних загадок, ребусів і розвивальних задач. Не другорядне місце займають софізми.
Для учнів 7-9 кл. можна запропонувати софізми такого типу:
- “Вага слона дорівнює вазі комара”
Нехай ![]() – вага слона,
– вага слона, ![]() – вага комара.
– вага комара.
Позначимо їх суму через ![]() :
: ![]() . З цієї рівності можна дістати ще дві:
. З цієї рівності можна дістати ще дві:![]() ,
, ![]()
Перемножимо почленно останні дві рівності:![]()
Додавши до обох частин цієї рівності по ![]() , дістанемо:
, дістанемо:
![]()
![]()
Добуваючи з обох частин рівності квадратний корінь, матимемо:
![]()
![]() тобто вага слона (х) дорівнюй вазі комара (у).
тобто вага слона (х) дорівнюй вазі комара (у).
- Софізм “Усі числа рівні між собою”.
Нехай a і b – два довільних числа і a>b. Тоді знайдеться таке додатне число c, що a=b+c. Помножимо цю рівність на (a-b)![]() .
.
![]()
![]()
![]()
Поділивши обидві частини рівності на ![]() отримаємо
отримаємо ![]() .
.
- Софізм “Кожний трикутник рівнобедрений”.
Нехай ABC – довільний трикутник. Проведемо бісектрису кута A і перпендикуляр до сторони ВС, що проходить через її середину D (рис.2). Ці дві прямі перетинаються, бо якщо вони паралельні, то трикутник рівнобедрений, отже, дальше доведення зайве. Позначимо через М точку перетину цих прямих. Розглянемо спочатку випадок, коли точка М розташована всередині трикутника. Проведемо з точки М перпендикуляри MF і ME на сторони АВ і АС. Тоді
![]() (1)
(1)
![]() (2)
(2)
З (1) випливає, що ![]() , а з (2) – що
, а з (2) – що ![]() , тому
, тому ![]() (3)
(3)
З (1) і (3) випливає, що
![]() (4)
(4)
![]() (5)
(5)
Додаючи рівності (4) і (5), дістанемо ![]() .
.
Коли точка перетину бісектриси кута ![]() і перпендикуляра до сторони
і перпендикуляра до сторони ![]() розташована поза трикутником
розташована поза трикутником ![]() , то доведення буде аналогічне, з тією лише різницею, що рівності (4) і (5) не додаються, а віднімаються.
, то доведення буде аналогічне, з тією лише різницею, що рівності (4) і (5) не додаються, а віднімаються.

![]() A
A
F E
![]()
F
В С
D
4. Софізм ![]()
Відомо, що ![]() ,
, ![]() .
.
Перемноживши почленно, дістанемо: ![]() . Виконуючи почленне ділення отримаємо
. Виконуючи почленне ділення отримаємо![]() .[11]
.[11]
4) творча дослідницька робота членів гуртка.
Сильніші учні на гурткових заняттях займаються творчою дослідницькою роботою. Прикладом такої роботи є знаходження учнями доведення тверджень, виведення формул. Зокрема учні 8 класу можуть попрацювати над питанням «Різні доведення теореми Піфагора» (існує 367 різних доведень).
Примірна тематика занять гуртка 7-9 класів, які можуть бути внесені до плану роботи:
- Роль математики в розвитку техніки. Математика на службі людини. Зв’язок розвитку математики з вимогами практики.
- Елементи історії геометрії.
- Різні доведення теореми Піфагора. Узагальнення теореми Піфагора – теорема Евкліда.
- Велика теорема Ферма.
- Окремі властивості натурального ряду чисел.
- Проблеми Гольдбаха-Ейлера
- З історії розвитку вчення про рівняння.
- Задачі на складання рівнянь.
- Від рахівниці до ноутбука.
- Залежність між середнім геометричним і середнім арифметичним кількох чисел.
- Теорема Безу.
- Магічні квадрати.
- Пучки і в’язки кіл
- Геометричні побудови з допомогою циркуля
- Періодичні десяткові дроби.
3.2 Математичні вечори
Найбільш масовою формою позакласної роботи з математики в школі є математичний вечір.
Найчастіше вечори бувають присвячені:
а) підбиванню підсумків учнівських математичних олімпіад;
б) окремим видатним математикам або питанню розвитку математики в деяких країнах;
в) питанням застосування математики;
Оскільки змістовний математичний вечір підготовити не так легко, то таких вечорів протягом одного навчального року організовують не більш двох.
Естетичним і цікавим повинно бути оголошення про проведення вечора. Можна, для прикладу, дату і час проведення записати у двійковій чи вісімковій системі числення. Щоб потрапити на вечір, учням пропонуємо придбати вхідні квитки. Ними є математичні загадки, жарти, задачі, шаради. Зміст задач підбираємо такий, що для їх розв’язання потрібно зосередити увагу і, звичайно, знати арифметичні дії. Такі задачі будуть цікавими для всіх учнів.
- Скільки кінців у трьох палок, у трьох з половиною?
- Поділити півсотні на половину.
- Півтора курки за півтора дня знесуть півтора яйця. Скільки яєць знесуть три курки за 4 дні.
- Одне яйце варять 4 хв., тоді воно вважається звареним. За скільки хв. можна зварити 5 яєць?
- Яке число треба поділити на свою п’яту частину, щоб дістати 5?
- Записати 100 за допомогою чотирьох дев’яток.
Ціна квитка – відповідь до задачі.
Тематика вечора може бути різноманітною. Для 7-9 класів:
- Математика на службі людини
- Розвиток математики в Україні
- Математика і хімія
- Жінки-математики
- Легенди про Піфагора та ін.
У плані вечора передбачають короткі доповіді по темі, КВВ, вікторини, декламування віршів з математичним змістом, виступи-жарти, матеріалом яких можуть бути, наприклад, невдалі спроби розв’язування задач, ігри,
математичні фокуси, задачі на відгадування задуманих чисел, демонстрування швидкої лічби.
Доповідь вечора присвяченого Піфагору Самоському (8кл) можна представити у вигляді таких презентацій (2-3хв):
- “Сторінками біографії Піфагора”.
- Гетерія Піфагора.
- Гармонія чисел – складова життя вченого.
- Теореми Піфагора.
- Піфагор і спорт.
Бажано написати відомі вислови Піфагора про числа: “Усі речі – числа”, “Де немає числа і міри – там хаос і химери”, “Наймудріше – це число”, “Числа керують світом”.
При плануванні другої (розважальної ) частини вечора потрібно врахувати тягу дітей до яскравого, таємничого і загадкового. Але неприпустимо, щоб в свідомості учнів те цікаве та веселе, з чим він знайомиться на вечорі, протиставлялося тому, що він вивчає на уроках. Тому потрібно давати відповідні пояснення.
На вище вказаному вечорі можна показати прийом швидкої лічби на ![]() .
.
Виступаючий пропонує кому-небудь з присутніх назвати двоцифрове число, кратне 9. Після цього він негайно записує результат множення названого числа на ![]() . Нехай, припустимо, хтось назвав число
. Нехай, припустимо, хтось назвав число ![]() . Тоді
. Тоді
![]() .
.
Пояснення. Число ![]() можна подати як
можна подати як ![]() , де
, де ![]() одне з чисел від 1 до 9. Отже,
одне з чисел від 1 до 9. Отже, ![]() . Таким чином, загадане число ділимо на 9 і результат виписуємо підряд 9 раз.
. Таким чином, загадане число ділимо на 9 і результат виписуємо підряд 9 раз.
Таке ж пояснення даємо до математичного фокусу:
На стіл покладено три фігури: куб, конус, піраміду. До стола підходить член математичного гуртка і пропонує кому – небудь з учнів узяти по одній фігурі, не дивлячись на них. Потім гуртківець пропонує кожному з учнів підрахувати число букв у назві взятих ними фігур і помножити його на 2 (учневі А.), на 10 (учневі Б.), на 11 (учневі В.). Потім треба визначити суму знайдених чисел і назвати її гуртківцеві. Дізнавшись про цю суму, гуртківець відразу
відгадує, яку фігуру взяв кожний з учнів.
Пояснення. Нехай у назвах фігур, узятих учнями А., Б., В.,
відповідно ![]() букв. Тоді
букв. Тоді![]() , бо
, бо ![]() . Припустимо що учні повідомили суму d.
. Припустимо що учні повідомили суму d.
Тоді ![]() і
і ![]()
Звідси ![]() і
і ![]() .
.
Внаслідок того, що ![]() , приходимо до висновку, що
, приходимо до висновку, що ![]() є часткою від ділення
є часткою від ділення ![]() на 9, а
на 9, а ![]() – остачею.
– остачею.
Можна включити демонстрування феноменальної пам’яті. Для свого виступу учень заготовив картки, на кожну з яких виписав числа такої таблиці:
|
23. 2 358 314 |
46. 5 505 505 |
68. 7 741 561 |
|
24. 3 369 549 |
47. 6 516 730 |
69. 8 752 796 |
|
25. 4 370 774 |
48. 17 527 965 |
70. 9 763 921 |
|
26. 6 381 909 |
49. 8 538 190 |
71. 886 404 |
|
27. 6 392 134 |
50. 9 549 326 |
72. 1 897 639 |
|
28. 7 303 369 |
51. 662 808 |
73. 12 808 864 |
|
29. 8 314 594 |
52. 1 673 033 |
74. 3 819 099 |
|
30. 9 325 729 |
53. 12 684 268 |
75. 4 820 224 |
|
31. 1 448 202 |
54. 3 695 493 |
76. 5 831 459 |
|
32. 1 459 437 |
55. 4 606 628 |
77. 6 842 684 |
|
33. 2 460 662 |
56 5 617 853 |
78. 7 853 819 |
|
34. 3 471 897 |
576 628 088 |
79. 8 864 044 |
|
35. 4 482 022.' |
58. 7 639 213 |
80. 9 875 279 |
|
36. 5 493 257 |
59. 8 640 448 |
81. 998 752 |
|
37. 6 404 482 |
60. 9 661 673 |
82. 1 909 987 |
|
38. 7 415617 |
61. 774 156 |
83. 2 910 112 |
|
39. 8 426 842 |
62. 1 785 381 |
84. 3 921 347 |
|
40. 9 437 077 |
63. 2 796 516 |
85. 4 932 572 |
|
41. 550 550 |
64. 3 707 741 |
86. 5 943 707 |
|
42. 1 561 785 |
65. 4 718 976 |
87. 6 954 932 |
|
43. 2 572 910 |
66. 5 729 101 |
88. 7 965 167 |
|
44. 3 583 145 |
67. 6 730 336 |
89. 8 976 392 |
|
|
45 4 594 370 |
|
90. 9 987 527 |
В якому-небудь кутку кожної картки проставляють номер числа. На початку виступу учень переглядає картки і робить вигляд, що він «запам'ятовує» написані на них числа. Картки перевертають написаним униз, присутнім пропонують узяти яку-небудь з них і назвати її номер. Після цього учень називає відповідне число.
Секрет цього «запам'ятовування» – у способі побудови таблиці, Перші дві цифри чисел дістаємо, додавши до номера картки число 9 і записавши результат у зворотному порядку (наприклад 27 +9= 36, а записати треба 63). Кожну наступну цифру числа знаходимо додаванням чисел, зображених двома попередніми цифрами, не рахуючи десятків:
63 9 2 1 3 4
6+3 3+9 9+2 2+1 1+3 [11]
3.3 Математичні вікторини
Математичні вікторини – популярна форма позакласної роботи, своєрідне змагання між учнями.
У доборі матеріалу для вікторини можливі два підходи: вправи для повторення всіх розділів вивченого курсу математики і вправи для повторення визначеної теми.
У вікторині можуть брати участь усі, хто бажає. Вікторину, залежно від числа учасників, можна проводити по-різному.
Перший варіант. Кожне запитання або задачу зачитує вчитель чи учень, який проводить вікторину. На обдумування відповіді дається декілька хвилин. Відповідає той, хто перший підніме руку. Якщо відповідь неповна, то можна дати можливість висловитись ще одному учаснику вікторини. За повну відповідь присуджують два очка, за неповну, але задовільну – одне очко.
Переможцями вважаються ті учасники вікторини (24 учні), які набрали найбільше число очок. Окремі задачі і запитання лише зачитують, умови інших задач можуть бути записані на дошці. Так можна проводити вікторину, коли в ній бере участь порівняно небагато (50 60) учнів.
Другий варіант. Якщо у вікторині бере участь багато (100200) учнів, то її проводять так: тексти всіх запитань і задач виписують (заздалегідь) на дошці або на окремих аркушах, які роздають учням. Кожному учасникові видають аркуш чистого паперу, на якому він записує відповідь та коротке пояснення до кожного запитання і задачі, а також своє прізвище, ім'я, клас.
Цей аркуш він здає журі вікторини. Через певний час після початку вікторини (наприклад, через 30 хв) приймання аркушів від учасників вікторини припиняють. Журі перевіряє розв'язання і виявляє переможців.
Поки журі проводить підсумки, можна провести декілька ігор, чи запропонувати інсценівку. Задачі для вікторини повинні бути невеликими, доступними для усного розв'язання. Крім задач, у вікторину можна включати також різні запитання з математики або з історії математики, задачі-жарти.
Для учнів 7 класів можна пропонувати такі запитання:
- У скільки разів двоцифрових чисел більше ніж одноцифрових?
-
Записати множину розв’язків нерівності
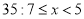 .
.
- Записати число 100 використовуючи 5 одиниць.
- Для яких двох цілих чисел сума більша за добуток?
- Знайти число, 17% якого більше від 14% його на 27.
- У кошику лежить 5 яблук. Чи можна поділити їх порівну між 5 товаришами так, щоб одно яблуко залишилося в кошику?
- Щука важить стільки, скільки важить кілограм та пів щуки. Яка вага щуки?
- З 8 однакових на вигляд куль, одна дещо важча за інші. Яка потрібна найменша кількість зважувань, щоб виявити цю кулю?
- Що таке «абак»?
- У квадраті відрізали один кут. Скільки кутів залишилося?
- Онукові 4 роки, дідусеві – 60. Через скільки років дідусь буде в 5 раз старший за онука?
- Ім’я якого відомого математика складається з трьох складів: перший склад – число, другий – нота, третій – одне з імен давньоєгипетського бога Сонця?
Переважно вікторини проводять на математичних вечорах, заняттях гуртка або в позаурочний час.
3.4 Математичні турніри та естафети.
Особливо жваво проходять на математичних вечорах командні змагання – турніри. З кількох (найкраще паралельних) класів організовують дві команди по 5 учнів у кожній. Ці команди готуються до змагання: добирають задачі і запитання, які пропонуватимуть своїм суперникам, індивідуальні і колективні виступи, креслять таблиці, унаочнення до задач тощо. На сцені одна команда розміщується з одного боку, друга – з іншого. Призначають ведучого і журі. Журі присуджує очки – за правильні відповіді, цікаві задачі, за оригінальні художні виступи тощо.
Спочатку ведучий може запропонувати кілька вправ обом командам (різних або однакових, залежно від запитань і, від того, як відповіла на те чи інше запитання перша команда).
Команди, кожна окремо, обговорюють ці запитання і приблизно через хвилину відповідають; спочатку представник першої, потім – другої. Після цього можна запропонувати їм перевірити свої відповіді.
Далі кожна команда дає по 3–5 запитань своїм суперникам. Журі оцінює і якість запитань, і відповіді на них, а в кінці підбиває загальний підсумок, визначає команду-переможця.
Трохи інакше проходять математичні естафети. Кожний з паралельних класів виділяє по 5 найкращих учнів, вони сідають за окремими столами по одному учню від класу і розв'язують перші задачі своїх варіантів. Хто розв'язав, відходить від стола, а на його місце сідає другий, учень цього самого класу і т. д. Дається певний час на розв’язання. Правильність розв'язання задачі перевіряють члени журі. Виграє команда, яка набере більше очок.
Командним змаганням є гра “Що? Де? Коли?”.
Для проведення гри “Що? Де? Коли?” формуються три команди по 5 учнів. Склад команди різноманітний, формується самими учнями , вони ж обирають капітана. До складу команди входять учні різновікових класів, не обов’зково відмінники, але обов’язково начитані, які глибоко і гнучко мислять.
Змагання складається з 7-9 раундів. В кожному раунді знатокам дається питання, наперед підготовлене учнями. Після двохвилинного обдумування граюча команда дає відповідь. Одночасно над запитанням думають і резервні команди. Вислухавши відповідь граючої команди, ведучий просить резервні команди висловити свою думку. Кінцевою відповіддю знатоків вважається остання гіпотеза. Оголошується правильна відповідь і виясняється, хто в данному раунді переміг: знатоки чи глядачі.
Якщо в раунді граюча команда відповіла правильно, вона залишається за столом лідера. В противному разі вона уступає своє місце тій команді, яка дала правильну відповідь. Якщо всі три команди відповіли неправильно, місце за столом лідера займає одна з команд, що залишилися, жеребкуванням.
Через кожні два раунди проводиться музична “пауза” по оголошенню ведучого або по показах стрілки рулетки. “Пауза” - це номер художньої самодіяльності. В кінці зустрічі ведучий оголошує команду переможця. Можуть розігруватися призи, виготовлені членами команд.
Для учнів 7-9 класів можна пропонувати запитання такого змісту:
- Математик випадково попав у невеличке містечко, яке було досить далеко розташоване від інших міст. Щоб якось вбити час, він вирішив постригтися. В місті були лише 2 перукарі. Заглянувши до одного майстра, математик побачив, що в його салоні брудно, сам майстер неохайний і неакуратно пострижений. В салоні другого перукаря було чистенько, сам він був ідеально одягнений і гарно пострижений. Подумавши, математик пішов стригтися до першого перукаря. Запитання: чим пояснити причину такого дивного рішення математика?
- Відомо, що маса тіла на Місяці в 6 раз менша ніж на Землі. Щоб перевірити це, один з космонавтів взяв з собою тіло, маса якого на Землі відома і вагу з гирями. Закон не підтвердився. Чим це пояснити?
-
У мене в руках ігрова карта: бубновий король. На карті ви бачите зображення ромба. Запитання: чому на картах бубнової масті зображено саме ромб, не щось інше?[11]
- Математичні олімпіади
Підсумком всієї позакласної роботи з математики є олімпіади. Її завдання – підвищити в учнів інтерес до вивчення математики, поглибити їх теоретичну підготовку, вплинути на розвиток їх творчих здібностей, виявити юних аматорів математики, щоб залучити їх у дальшому до наукової роботи.
Разом з тим математичні олімпіади мають і виховне значення. Вони привчають учнів до організованості, зміцнюють волю до перемоги, виробляють самостійність і чіткість мислення.
На олімпіаді дають розв'язувати задачі і приклади в обсязі програми з математики відповідного класу. Проте умови задач та їх зміст – не стандартні. Щоб розібратися в них, учасникам треба вміти самостійно мислити, мати добре розвинуту геометричну уяву, знати найраціональніші перетворення і т. д.
У число задач до олімпіади можна включити одну-дві такі, які могли б розв'язати більшість учасників. Надміру складне завдання може породити в учня невіру в свої сили і відбити охоту займатися математикою. Але водночас доцільно давати й складніші задачі, щоб з усієї маси учасників виділити найбільш підготовлених. Найкраще пропонувати 3–5 задач різної трудності нестандартного змісту. Шкільні олімпіади проводяться в два або три тури.
Учнів ознайомлюють з умовами олімпіади:
- До участі в олімпіаді запрошуються учні 7—9 класів. Кожний учасник розв'язує лише задачі, призначені для відповідного класу.
- Олімпіада проводиться за три тури:
І тур — з 1 до 8 лютого; II тур — з 15 до 22 лютого; III тур - 4 березня. На розв'язування задач III туру буде відведено 3 год.
- Право участі в II турі дістає той учень, який набере не менш як 2/3 числа очок, установлених за всі задачі і приклади першого туру. Список учасників II туру буде оголошено 11 лютого,
- Право участі в III турі дістануть учні, що наберуть не менш як 2/3 очок, установлених за задачі II туру. Список учасників III туру буде оголошено 25 лютого.
- Переможцем олімпіади серед учнів відповідного класу вважатиметься той, який у III турі набере найбільшу кількість очок. Учні, що займуть перше, друге і третє місця, будуть нагороджені грамотами і премійовані подарунками.
Поряд з цим оголошенням вивішують тексти задач і прикладів І туру. Визначають також останній день прийому розв'язків і місце, куди їх треба здавати. У примітці зазначають день оголошення завдань II туру олімпіади.
Наведемо примірні завдання для учнів 8 класу на І, II і III турах шкільної математичної олімпіади.
І тур
1. Двом трактористам дано завдання зорати по 2,5 га землі. Перший тракторист перевиконав завдання на 10%, а другий зорав на 0,2 га більше, ніж перший. На скільки процентів перевиконав своє завдання другий тракторист? (4 б).
2. Знайти остачу від ділення ![]() на 7. (5 б).
на 7. (5 б).
3. Сторони прямокутника — цілі числа. Яка повинна бути їх довжина, щоб периметр прямокутника чисельно дорівнював його площі? (5 б).
4. Довести, що вираз ![]() додатний, якщо а і b одночасно не дорівнюють нулю (4 б).
додатний, якщо а і b одночасно не дорівнюють нулю (4 б).
5. Побудувати трикутник, знаючи положення середин його сторін. (З б).
-
тур
- Через дві суміжні вершини квадрата проведено коло так, що дотична до нього з третьої вершини дорівнює подвоєній стороні квадрата. Знайти радіус цього кола, якщо площа квадрата дорівнює 10. (5 б).
- На яке число треба помножити 333667, щоб дістати число, яке записується самими вісімками? (4 б).
- Через точку всередині кута провести пряму так, щоб її відрізок, обмежений сторонами кута, поділявся цією точкою в даному відношенні. (4 б).
-
Довести, що при довільному натуральному п вираз
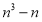 ділиться на 6.
ділиться на 6.
- б).
-
Корені
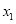 і
і 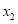 рівняння
рівняння 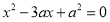 такі, що
такі, що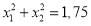 . Обчислити значення а. (З б).
. Обчислити значення а. (З б).
III тур
-
Побудувати трикутник за стороною а, медіаною
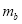 і висотою
і висотою 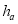 (4 б).
(4 б).
-
Не розв'язуючи рівняння
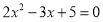 , скласти нове рівняння, корені якого дорівнювали б
, скласти нове рівняння, корені якого дорівнювали б  і
і 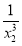 , де
, де 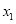 і
і 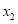 – корені даного рівняння. (4 б).
– корені даного рівняння. (4 б).
- Довести, що коли опуклий чотирикутник має вісь симетрії, то можна або в нього вписати коло, або описати коло навколо нього. (4 б).
Крім шкільних олімпіад, учнів потрібно залучати до участі у заочних олімпіадах, які проводять вищі навчальні заклади. Не другорядну роль у підвищенні інтересу до знань відіграє всеукраїнський інтерактивний конкурс «Кенгуру», який проводиться щороку за завданнями з обласного оргкомітету конкурсу.
- Математичні екскурсії
Екскурсія повинна переконати учнів, що набуті ними в класі теоретичні знання мають конкретні застосування в різних галузях промисловості, у сільському господарстві і в побуті. Під час екскурсії учні пересвідчуються, що такі, наприклад, геометричні поняття, як круг, трикутник, многокутник, сфера, многогранник, застосовуються в багатьох деталях машин, у спорудах, верстатах різноманітного призначення. Вони зустрічаються з необхідністю знаходження за вивченими ними формулами площ і об'ємів тіл, застосування відомих їм теорем і співвідношень, Поряд з цим, вони пересвідчуються, що практична діяльність людей ставить багато питань, які треба розробляти теоретично, що теорія і практика – нерозривно зв'язані між собою.
У шкільній практиці можна зустріти переважно два види екскурсій: у природу і на виробничі об'єкт. Як перші, так і другі можуть мати різну тематику. Наприклад, екскурсію в природу можна провести на такі теми: математика в лісі, математика на березі річки, математика у відкритому полі.
Так у 8 класі можна на екскурсії в природу визначити висоту дерева, коли основа доступна і недоступна, знаходити відстань між двома недоступними деревами, встановлювати азимут напрямку на деякий об’єкт. У 9 класі можна діаметр стовбура дерева, площі земельних ділянок. При проведенні екскурсій на тваринницьку ферму у 9 класі визначають об’єм скирти, бочки, місткості відра. Вчитель проводить бесіди про завдання екскурсій, вказує на необхідні інструменти та теоретичні знання. Обов’язково треба робити підсумок проведення екскурсії.
ВИСНОВКИ
В даній курсовій роботі встановлено зміст та принципи позакласної роботи з математики, виділені напрямки її реалізації. Розглянуті види позакласної роботи для учнів, що відстають від інших у вивченні програмного матеріалу та для учнів, що виявляють до математики підвищену цікавість і здібності. На прикладах шкільної практики навчання математики охарактеризовано і продемонстровано форми організації позакласної роботи, зокрема: гурткова робота, математичні вечори, математичні вікторини, математичні турніри й естафети, математичні стінгазети, математичні олімпіади. Отже, позакласна робота — це складова частина навчально-виховного процесу в школі, одна з форм організації вільного часу учнів.
1


про публікацію авторської розробки
Додати розробку
