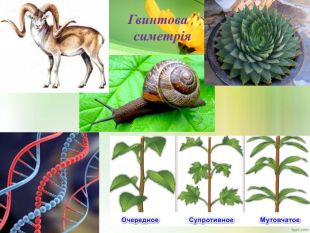
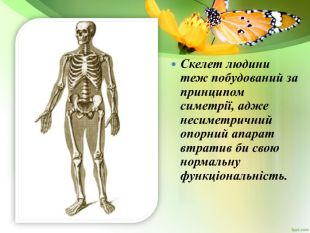
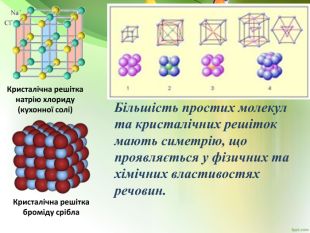
Позакласний захід "Симетрія навколо нас"

поряд з нами. Симетрія Вчитель математики. Криворучко Тетяна Вікторівна. Базаліївський ліцей

Симетрія - окраса світу

Симетрія. В давнину це слово використовували як “ гармонія”, “краса”. А й справді з грецької мови воно означає «відповідність, пропорційність, подібність в розташуванні частин».

Симетрія в природі

Природа - дивовижний творець і майстер. Все живе в природі має властивість симетрії.

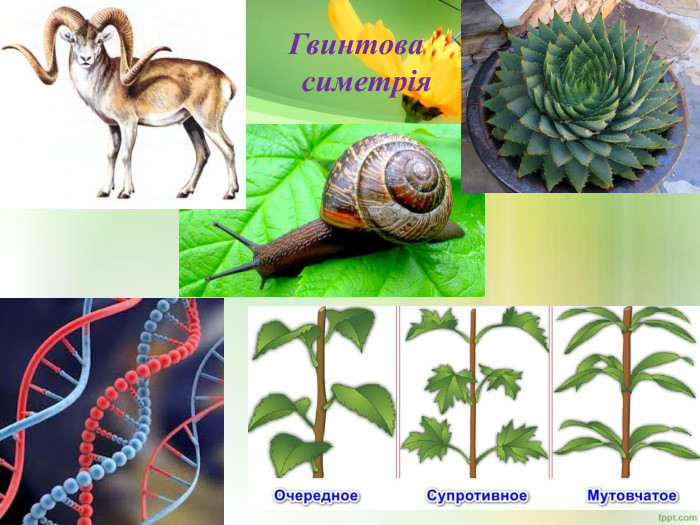
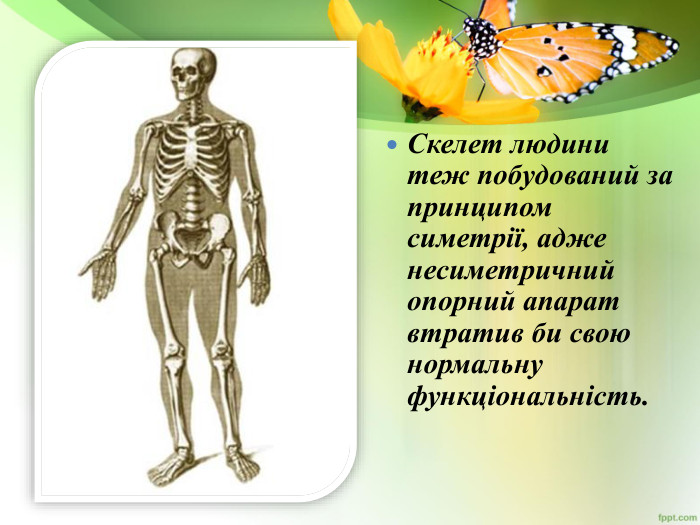
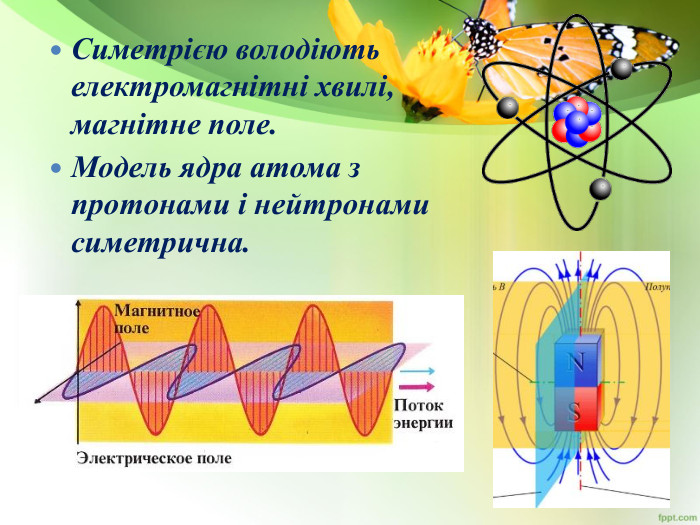
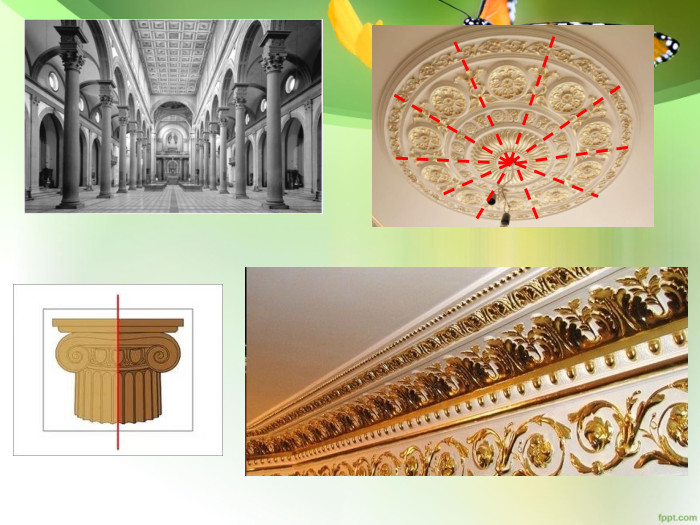
Якщо зверху подивитися на будь-яку комаху і подумки провести посередині пряму (площину), то ліві і праві половинки комах будуть однаковими і по розташуванню, і за розмірами, і за забарвленням. Адже ми ні разу не бачили, щоб у жука або бабки, у будь-якої іншої комахи лапи ліворуч були б ближче до голови, ніж праворуч, а праве крило метелика або сонечка було б більше, ніж ліве. Такого в природі не буває, інакше б комахи не змогли б літати.

Яскраво вираженою симетрією володіють листя, квіти, гілки, плоди. Дзеркальна симетрія характерна для листя, але зустрічається і у квітів.

Симетрія, характерна для представників тваринного світу, називається білатеральною симетрією.

Одним з різновидів кристалу є сніжинка. Форма сніжинок може бути різноманітною, але всі вони мають дзеркальну симетрію.

У живій і неживій природі симетрія зустрічається дуже часто. Це зумовлено способом існування – несиметричні комахи і птахи не змогли б літати, листочки у рослинах затіняли б одне одного. Центральна і поворотна симетріїАденовірус. Медуза

Осьова симетрія

Центральна, осьова і гвинтова симетрії у вимерлих найпростіших одноклітинних організмах – радіоляріях.

Гвинтова симетрія

Дзеркальна симетрія

Скелет людини теж побудований за принципом симетрії, адже несиметричний опорний апарат втратив би свою нормальну функціональність.

Симетрія у хімії

Більшість простих молекул та кристалічних решіток мають симетрію, що проявляється у фізичних та хімічних властивостях речовин. Кристалічна решітка натрію хлориду(кухонної солі)Кристалічна решітка броміду срібла

Проте симетрія існує і там, де її не видно на перший погляд. Фізик скаже, що всяке тверде тіло - кристал. Хімік скаже, що всі тіла складаються з молекул, а молекули складаються з атомів. А багато атомів розташовуються в просторі за принципом симетрії.

Симетрія многогранників яскраво проявляється у структурі мінералів

Симетрія у фізиці і техніці

Жоден з технічних засобів – від шестерні до ракети – не працював би без симетрії!

Симетрією володіють електромагнітні хвилі, магнітне поле. Модель ядра атома з протонами і нейтронами симетрична.

Галактики і квазари мають симетричну будову. Магнітне поле Землі теж симетричне відносно полюсів. Галактика Молочний шлях. Найстаріша галактика А1689 В11. Їй 2,6 млдр.років. Квазари

Симетрія в архітектурі

Вибираючи симетричні форми, архітектори прагнули досягти природної гармонії , як ознаки стійкості та рівноваги. Тадж-Махал, Індія. Собор Паризької БогоматеріПантеон

Храм Лотоса в ІндіїБашти Петронаса у МалайзіїЕйфелева вежа у Парижі, Франція

Приклад використання симетрії у садово-парковому мистецтві – топіарії.

Церква всіх святих у Києві та її план. Палац Розумовського у БатуриніДержпром, м. Харків. Палац Тарновських у Качанівці

Симетрія у мистецтві і побуті

Щодня у побуті ми стикаємося з проявами симетрії. Без симетрії не стояв би стілець, не трималися б окуляри, гвинт неможливо було б вкрутити.

Килими, мереживо, витинанки, розписи на стінах та декоративному посуді, прикраси – це теж прояв досконалості через симетрію.

Симетрія в українській вишивці

Симетрія в філології

Симетрія літер

Амбіграма (від лат. ambi — «подвійний», і грец. gramma — «буква») — каліграфічний візерунок, що дозволяє поєднати два різні прочитання з одного і того ж набору ліній.

Числові амбіграми називаються сторобограмами.

Літературним праобразом амбіграм можна вважати паліндроми — слова або фрази, які читаються однаково як зліва направо, так і справа наліво.

Симетрія в історії

Пізнавальну силу симетрії оцінили філософи Стародавньої Греції, використовуючи її в своїх теоріях. Так, наприклад філософ, Анаксимандр з Мілета, який жив у першій половині VI ст. до н. е., використовував симетрію в своїй космологічної теорії, де в центрі світу помістив Землю - головне, на його думку, тіло світу. Вона повинна була мати досконалу, симетричну форму, форму циліндра, а на периферії обертаються величезні вогняні кільця, закриті повітряними хмарами і дірками, які і здаються нам зірками. Земля розташована точно в центрі, і тут симетрія має сенс рівноваги.

Леонардо да Вінчі не оминув своєю увагою і симетрію. Він розглянув рівновагу кулі, що має опору в центрі ваги: дві симетричні половини кулі врівноважують одна одну, і куля не падає. Як художник він головну увагу приділяв вивченню законів перспективи і пропорцій, за допомогою яких виявляються художні достоїнства творів мистецтва.

Ф. Клейн запропонував взяти ідею симетрії як єдиного принципу при побудові різних геометрій. Клейн розвинув свою концепцію у фізиці і механіці. Програма Клейна як завдання пошуку різних форм симетрії виходить за рамки не тільки геометрії, але і всієї математики в цілому, перетворюється в проблему пошуку єдиного принципу для всього природознавства.

Знання збираються по краплині, як вода в долиніУкраїнське прислів’я