Презентація "Подібність фігур. Гомотетія"
Про матеріал
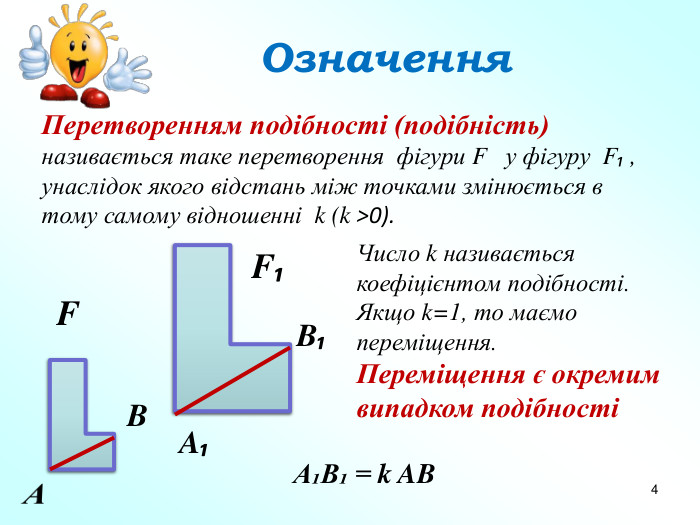
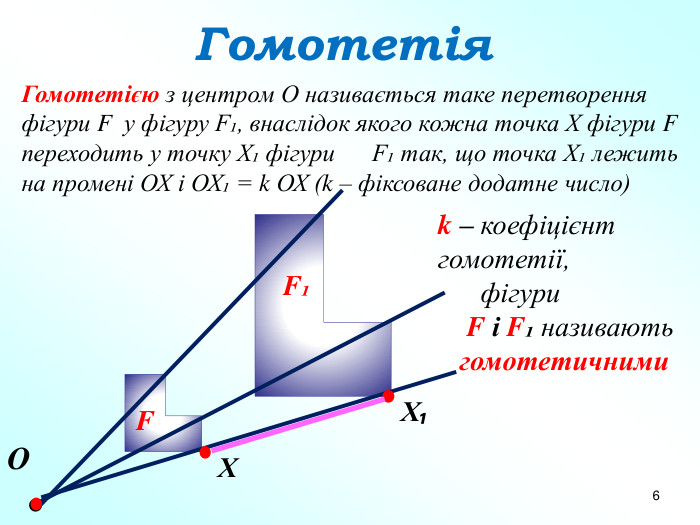
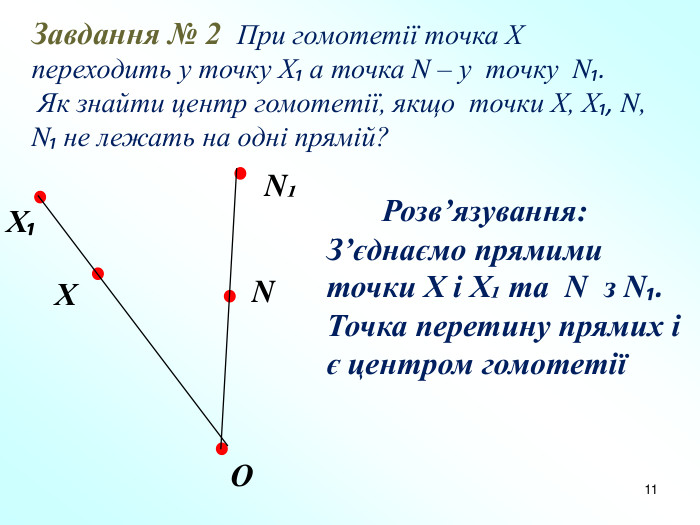
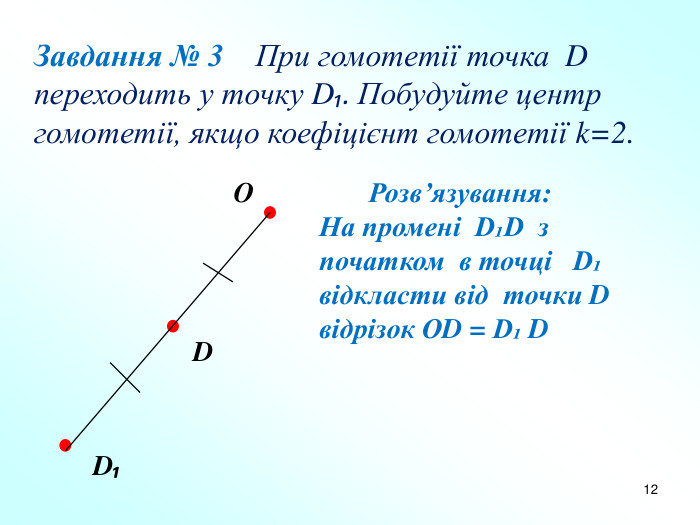
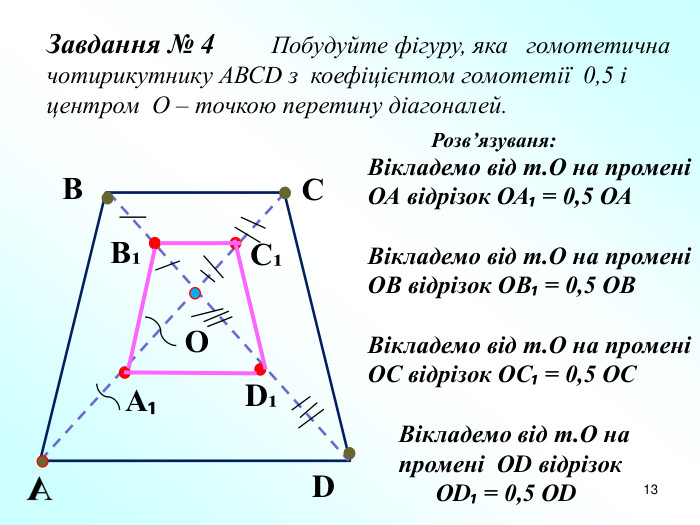
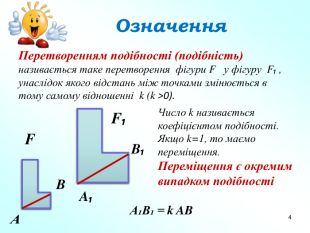
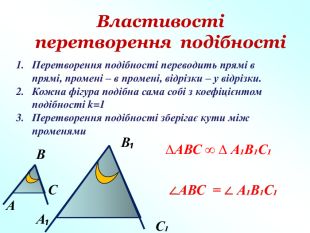
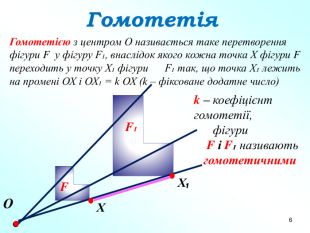
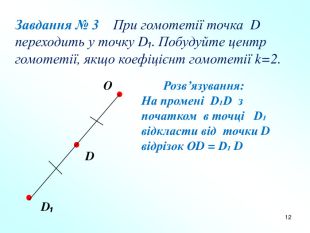
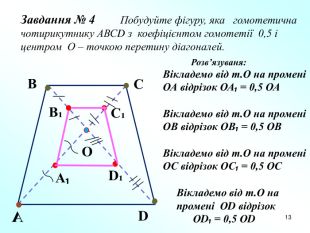
Презентація "Подібність фігур. Гомотетія" допоможе вчителям в доступній формі пояснити дану тему дев'ятикласникам. Пояснення супроводжується вправами на закріплення основних ознак та властивостей подібних фігур. Перегляд файлу
Зміст слайдів
ppt
До підручника
Геометрія 9 клас (Єршова А. П., Голобородько В.В., Крижановський О.Ф., Єршов С. В.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку