Сценарій творчого вечора математики

“Студія цікавих зустрічей “Колесо життя”

Розробила викладач математики Пасічник О. В.

1. Опис позакласного заходу

Захід проходить у вигляді телевізійної програми. На початку звучить фонова музика. Двоє ведучих представляють назву, знайомлять глядачів з учасникамиекспертами. До участі в програмі по-черзі запрошуються гості. Гості у своїх запитаннях-виступах демонструють зв'язок математики з різними галузями життя. Коментарі до їх виступів надають експерти. Дискусії між ними коментують ведучі. Присутні глядачі спостерігають за зйомками телевізійної програми. 

 

Тема: “Краса математики” Мета: 

Обладнання:

Вивіска з назвою студії  

Декорації: книжкова полиця, глобус, кубик Рубика, мольберти з висловами та фотографіями

Камера і оператор

Проектор

Переносна дошка з плакатами для демонстрації

Мольберт і картина, портрет Гаусса, лупа

Презентації для виступів

Гітара

Столик для експериментів

На столах глядачів роздатковий матеріал (в кінці)

Музичний супровід

Розваги для глядачів (рекламні паузи) Тривалість: 60 хв

 

Учасники:

Ведучий, 

Скептик (суддя в дискусіях),

Експерти 

1.                     Музикант і композитор 

2.                     Мистецтвознавець 

3.                     Доктор фізико-математичних наук 

4.                     Головний редактор журналу “Наука і життя” 

Гості:

1.                     Музикант (математика і музика) 

2.                     Художник, майстер живопису (математика і мистецтво) 

3.                     Провідний будівельник (математика і будівництво)

4.                     Архітектор (математика і архітектура)

5.                     Дослідник (демонструє Лист Мебіуса) 

 

                 

Вступне слово вчителя

Доброго дня, шановні студенти та гості нашого свята! Ми раді вітати Вас на творчому вечорі математики. Хочу розповісти вам невелику філософську притчу.

Якось професор філософії на своїй черговій лекції взяв скляну банку й наповнив її камінням, кожний з яких був не менше трьох сантиметрів у діаметрі.

Після чого запитав студентів, чи повна банка?

Всі відповіли: так, повна.

 Тоді він відкрив банку горошку й висипав її вміст у більшу банку. Горошок зайняв вільне місце між камінням. Ще раз професор запитав студентів, чи повна банка?

 Всі відповіли: так.

 Тоді він взяв коробку з піском, і висипав її в банку. Природно, пісок зайняв повністю існуюче вільне місце.

 У черговий раз професор запитав студентів, чи повна банка? Відповіли: так, і цього разу однозначно, вона повна.

 Тоді з-під стола він дістав склянку із водою й вилив її в банку до останньої краплі, розмочуючи пісок.

 Студенти засміялися.

 А зараз я хочу, щоб ви зрозуміли, що банка - це ваше життя. Камені - це найважливіші речі вашого життя: родина, здоров'я, друзі, діти - все те, що необхідно, щоб ваше життя залишалося повним навіть у випадку, якщо все інше втратиться. Горошок - це речі, які особисто для вас стали важливими: робота, дім, автомобіль. Пісок - це все інше, дрібниці.

 Якщо спочатку наповнити банку піском, не залишиться місця, де могли б розміститися горох і камені. І також у вашому житті, якщо витрачати увесь час і всю енергію на дрібниці, не залишається місця для найважливіших речей. 

Займайтеся, насамперед, каменями, тобто найважливішими речами в житті; визначите ваші пріоритети: інше - це тільки пісок.

 Тоді одна студентка запитала професора, яке значення має вода?

 Професор посміхнувся.

 - Я радий, що ви запитали мене про це. Я це зробив для того, щоб довести вам, що, як би не було ваше життя зайняте, завжди є трохи місця для дозвілля ;). 

Я вважаю, що нема границі досконалості. Черпайте для себе усе саме цінне.

Сьогодні ми хочемо вам довести, що математика – це частина нашого життя.

Математика в житті людини займає особливе місце. Ми настільки з’єдналися з нею, що навіть не помічаємо її. Сподівають, що сьогодні ви почерпнете для себе багато цікавого та корисного. Тож запрошуємо Вас на зйомки телевізійної програми “Колесо життя”. Тож бажаємо усім приємного перегляду.

 

Скептик: (звучить музика) Безкрайні простори Всесвіту…Постійний, щосекундний хід подій, які підкоряються певним законам світотворення. Космічні швидкості і прискорення, траєкторії і вектори, математичні функції і рівняння, нескінченний світ закономірностей і мова, на якій написана книга природи – математика!

 Під аплодисменти виходить ведучий телепрограми  із портфелем та лупою. Ставить портфель на столик.

-                    Ведучий: Ми раді вітати вас у студії цікавих зустрічей “Колесо життя”. Ну що ж, мої дорогі глядачі… Судячи по математичному блиску у ваших очах (прикладає лупу до ока) мені не даремно випала нагода зняти цю передачу. Я знаю, що кожен із вас ставив собі або вчителям питання такого типу: “Навіщо мені це потрібно?”, “Де можна застосувати це у житті?”. Тому сьогоднішню нашу програму  ми вирішили назвати так:

-                    Скептик: “Краса математики”.

-                    Ведучий: Прекрасний німецький математик Карл Гаусс (демонструє портрет на слайді) назвав математику царицею всіх наук.

-                    Скептик: Так і всіх…

-                    Ведучий. Уяви собі….Багато хто думає, що математика потрібна для того, щоб рахувати. Але це не так. Адже це дуже гармонічна наука. І ми сьогодні доведемо вам, що математика….(по-черзі) – це:

-                    Кібернетика

-                    Кораблі

-                    Мова техніки

-                    Рух землі

-                    Філософія

-                    Зореліт

-                    Мова Всесвіту

-                    Політ

-                    Літочислення -     Майбуття

-                    Мова числення

-                    Сприйняття

-                    Око хімії

-                    Відкриття

-                    Мова істини -       Це життя!

Фонова музика

 

-                    Ведучий: Хочу представити експертів сьогоднішньої розмови:

Мистецтвознавець: _________________

Музикант і композитор: __________________

Доктор фізико-математичних наук: __________________ 

Головний редактор журналу “Наука і життя”: __________________  

Ведучий: Отже, запрошуємо у студію першого гостя – музиканта ___________________.

Вихоить гість з гітарою, грає декілька акордів, потім звертається до гостей:

-                    Гість Музикант: Я займаюся музикою, захоплююсь літературою  і нещодавно прочитав, що Сальєрі (і не тільки він) використовував в музиці математику. Мене цікавить питання: в музиці справді є математика, чи Пушкін усе вигадав?

-                    Ведучий. Стоп. Ви маєте на увазі самого російського поета Пушкіна?

-                    Гість Музикант:  Так. Ось послухайте.. (зачитує уривок вірша під фон музики)

-                    Ведучий. Я думаю, що допоможе розібратися в цьому питанні наш експерт – музикант і композитор ________________.

-                    Експерт музикант: Першим, хто спробував показати красу музики за допомогою чисел був …. Піфагор. слайд

Він вивчав інтервали. Відкривав математичні відношення між окремими звуками, використовуючи при цьому особливий інструмент – монохорд. (слайд) Одна струна служить для зрівнювання тонів, друга натягується за допомогою гирі. Підвішуючи різноманітні гирі або натягуючи більш товсту струну змінюють звук струни, що досліджують, звіряючи його з тоном іншої струни. Виводять різні закони коливання струн. Досліди Піфагора лягли в основу науки, яку зараз називають акустикою.

-                    Скептик: Самі важливі математичні  закони музики – це ритм і тривалість. Той, хто не знайомий з дробами не зможе зрозуміти ноти. Допоможіть нам розібратися.

-                    Експерт музикант: Отже, шістнадцята, восьма, четвертна, половинна, ціла ноти.(Демонструє указкою біля дошки великі листки із нотами). Назви тривалостей служать одночасно і назвами чисел. Ціла нота – одиниця, тобто вона триває цілий такт. Половинна нота триває пів такта. Одна четверта триває 1/4 такта і т.д. Ми бачимо, що тривалості виникають як дроби: в результаті ділення цілої ноти на долі, тому тривалість можна підраховувати як дробові числа. Ну наприклад 1/4 =1/8+2/16….

-                    Ведучий: Відомо, що в  музиці як і в математиці зустрічаються паралелі. Перш за все в нотному записі – це 5 прямих, що утворюють нотний стан.

-                    Скептик: А чому ноти приходиться розташовувати на паралельних прямих?

-                    Експерт музикант: Музиканта цікавить не просто те, що одна нота вище чи нижче, йому необхідно знати на скільки саме вище чи нижче.

-                    Ведучий. Розглядаючи цей зв’язок глибше, можна помітити, що музика просто немислима без математики. Тепер ви (звертається до гостя-музиканта) зрозуміли до чого тут математика?

Гість: Справді, ніколи не думав, що в музиці закладено математичний

зміст.

-                    Скептик: Говорять, що Ейнштейн, (слайд) міркуючи над проблемами теорії відносності, любив грати на скрипці. І саме в такі хвилини зародилася його геніальна ідея.

-                    Експерт музикант: Ще один цікавий факт. Доведено що діти, які займаються музикою, краще засвоюють математику, зокрема геометрію. Це тому, що навчання музики пов’язане з розумінням, запам’ятовуванням, читанням нотних текстів, які складаються переважно з символів. Навички, сформовані в такий спосіб, полегшують засвоєння математичної символіки. 

-                    Ведучий: Дорогі глядачі! Робіть висновки: гра на музичному інструменті безпосередньо перед виконанням домашніх завдань є своєрідним “гімнастичним тренажером” для мозку, підготовкою його до продуктивної праці, а можливо – і для геніальних відкриттів.

-                    Скептик: Піфагор виявився правим, музика – це політ уяви та фантазії, який упорядкований чіткими формулами та графіками.

-                    Ведучий. Отже, робіть  висновки.

 Фонова музика  

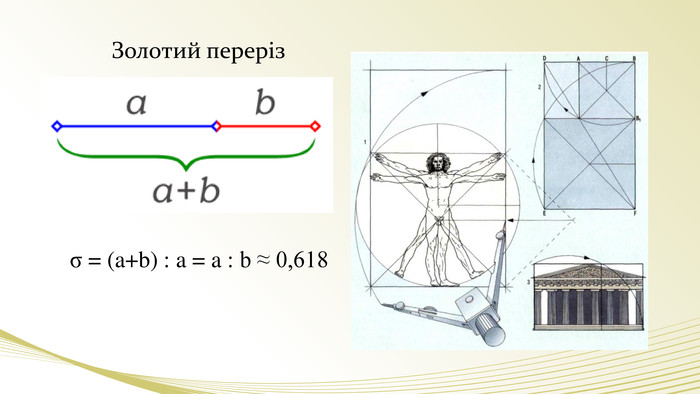
-               Ведучий: Великі твори мистецтва, візерунки й вигадливі форми, які зустрічаються в природі, багато століть захоплюють людство своєю красою та гармонією. А що створює цю гармонію?  Ну що ж після короткої рекламної паузи ми повернемося у студію, і зустрінемося із ще одним гостем щоб відповісти на запитання  “Що таке золотий переріз?”.

 

Показ мультфільма про науку (4 хв) Коментує скептик

 

-               Ведучий. Отже, хочу представити нашого наступного гостя  – художника, майстра живопису ____________________.

-               Гість художник: (Виходить з картиною, переглядає її і показує усім і ставить на мольберт) ну що скажете? 

-               Ведучий. Красиво, що тут скажеш?

-               Гість художник: А що таке по-вашому краса? 

-               Скептик: Мммм ….  А що це  має якесь відношення до математики? 

-               Гість художник:  Та ви що? Краса має саме безпосереднє відношення до математики, адже краса – це гармонія. А гармонія перекладається як порядок і співрозмірність. Тобто красиве завжди має особливі відношення і пропорції, які приємні для нашого ока, а значить основані на математиці. В основі краси і гармонії лежить золотий переріз. 

-               Ведучий. Золотий переріз? Думаю, що розібратися в цьому нам допоможе експерт в галузі красивого – мистецтвознавець _______________.

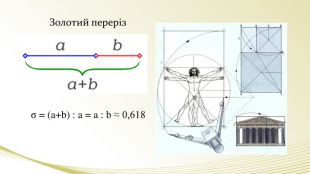
Експерт мистецтвознавець. Золотий переріз – це таке ділення відрізка на нерівні частини, при якому весь відрізок відноситься до більшої частини, як сама більша частина відноситься до меншої. (демонструє на слайді) - Скептик:  А де ж в картині ці відрізки?

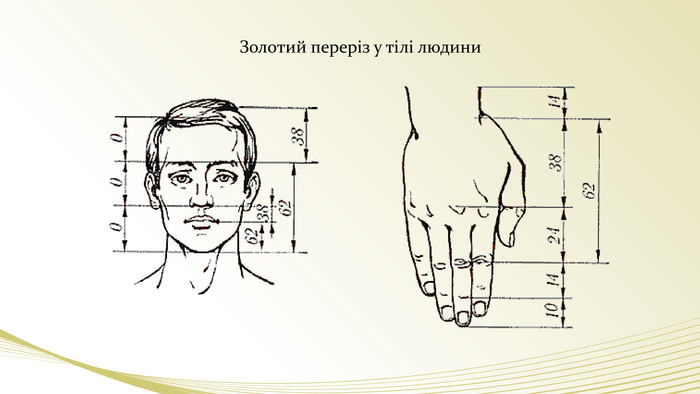
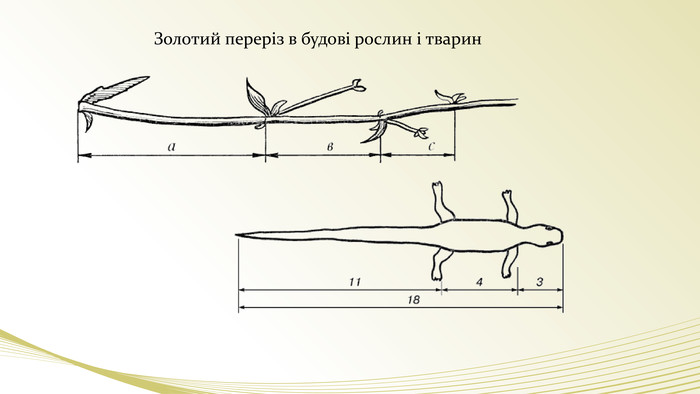
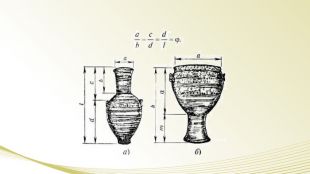
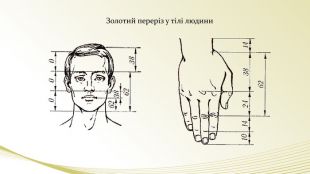
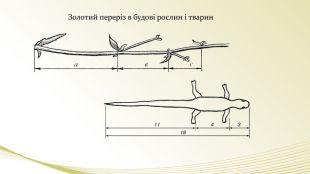
-               Експерт мистецтвознавець. Не треба приймати все так буквально. Такий принцип відношень лежить в основі самих різноманітних фігур, тому що він самий гармонічний. (слайд) Наприклад, є поняття золотого трикутника, золотого прямокутника, золотої спіралі. Композиція портрета Мони Лізи побудована на золотих трикутниках (слайд), а картина Рафаеля – на золотій спіралі(слайд). Те саме стосується споруди(слайд), скульптури(слайд), посуду(слайд),  будови тіла людини (слайд), рослин і тварин (слайд). 

-               Ведучий: А коли виникло це поняття “Золотого перерізу”?

-               Художник: (говорить, а в цей час демонструється відео) Леонардо да Вінчі, створюючи свої картини, використовував особливий принцип структурної досконалості. Він називав його золотим перерізом, при якому відношення більшого відрізка до меншого, а всього відрізка до більшого дорівнювало 0,618. За довго до цього в 6 ст. до н. е. давньогрецький філософ і математик Піфагор знаходить це відношення в геометрії, оглянувшись ще 300 років назад ми знайдемо згадки про нього у древніх єгиптян: вини називали її божественною суттю. 

-               Ведучий: Чи не означає це, що великим геніям усього людства були відкритті знання про існування особливих законів гармонії.

-               Мистецтвознавець: Дійсно, ця гармонія лежить всередині всього світостворення,  основі всього досконалого в нашому світі.

-               Скептик:  То що художники спеціально все прораховували?

-               Експерт мистецтвознавець. Так! Деякі спеціально, як наприклад Малевич перед тим, як малювати писав на холсті формули відношень, а деякі інтуїтивно, тому що відчували гармонію від природи.

-               Скептик:   Архівражаюче! 

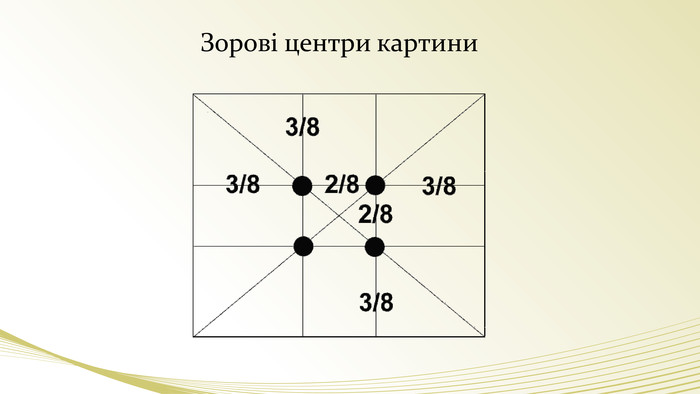
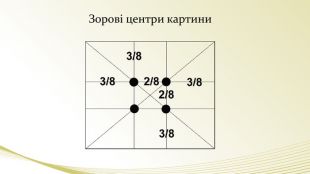
-               Експерт мистецтвознавець. В епоху Відродження художники відкрили, що будь-яка картина має певні точки, що приковують погляд, так звані зорові центри.(слайд) При цьому, не має значення який формат має картина – горизонтальний або вертикальний. Таких точок всього чотири, вони розташовані на відстані 3/8 і 5/8 від відповідних країв площини.

-               Художник  (Демонстрація картин) Як бачите, лінія горизонту на жодному з полотен не проходить по середині.  Вона обов'язково ділить його на частини, відношення площ яких 0,618... Саме таке відношення виявляється сприятливим для сприйняття зображення глядачами.

-               Експерт мистецтвознавець: Сьогодні кожен живописець користується законами божественної міри краси.

-               Ведучий: ви сказали про число 0, 618. Звідки про нього дізналися?

Прошу – коментар доктора наук. 

Експерт доктор наук: Так, дійсно, це число отримало назву “золотого”. (відео) Італійський математик Фібоначчі, досліджуючи різні явища природи,  відкрив нескінченну послідовність чисел, які мають деяку особливість: кожне з них є сумою двох попередніх. 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … і т. д. поділивши будь-яке менше число на сусіднє більше, ми завжди отримаємо 0, 618.  Золотий переріз зустрічається частіше, ніж ви того бажаєте. Усі екрани моніторів телевізорів і ноутбуків мають екран, де відношення висоти до ширини дорівнює 0,6.

-               Ведучий: Така закономірність дійсно вражає. Давайте переглянемо відео.

(демонстрація відео про числа Фібоначчі)

 

-               Скептик: Отже, як ми побачили, закони гармонії виражені математикою.

Фонова музика…

-               Ведучий: Відомі золоті пропорції в архітектурі. Зустрічайте нашого наступного гостя – архітектора фірми “Нова лінія” ______________________.

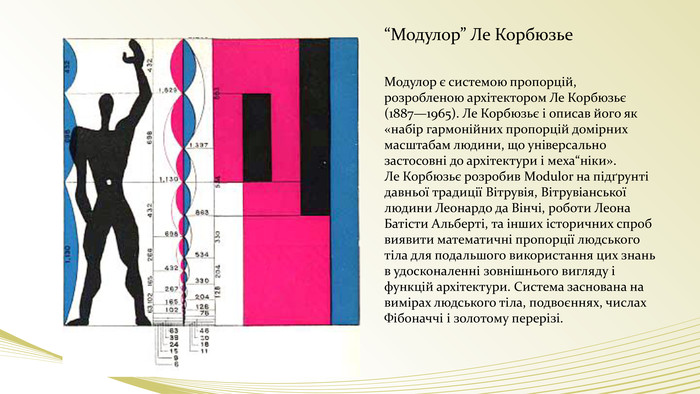
-               Гість архітектор: Дякую. Правило золотого перерізу завжди застосовували кращі архітектори, художники і митці всього світу для гармонійного розподілу цілого на взаємопов'язні частини. Зокрема, відомий архітектор Ле Корбюзье винайшов систему пропорцій, що називається модулором. (слайд)

-               Ведучий: Тобто ви хочете сказати, що ця система заснована на вимірах людського тіла? - Гість архітектор: І не тільки. Ще на числах Фібоначчі і золотому перерізі. Думаю, кожна людина розуміє, що математичні розрахунки та обчислення, що проводили провідні інженери-математики,  - це канва  створення таких архітектурних шедеврів, які ми бачимо. 

-               Скептик: тут не посперечаєшся. Дійсно, в основу архітектурних споруд закладені пропорції. 

-               Ведучий. Усі видатні майстри архітектури опиралися і опираються на принципи розрахунку розмірів, і вони допомагають наблизитися їм до гармонічної форми. (коментує слайди) Давайте поринемо у чарівний світ гармонії та пропорції)

-               Скептик: Правий був Ле Корбюзьє, який говорив: Математика – це велична споруда, створена уявленням людини для пізнання Всесвіту. - Ведучий: А що це за інструмент ви тримаєте у руках?

-               Гість архітектор. Це інструмент античного майстра - пропорційний циркуль. Я його змайстрував сам і назвав Циркуль золотого перерізу. Він

допомагає завжди керуватися золотим перерізом, якщо ви щось робите. Такий маленький інструмент може принести багато відкриттів про навколишній світ. 

-               Скептик: Доречі,  аналог  досі зберігаються в музеї Рима та Мюнхена. 

-               Ведучий: Тобто нас оточує математика, просто ми цього не помічаємо. 

-               Скептик: Але сьогодні багато столиць світу прикрашають архітектурні шедеври зовсім непропорційні. Такі будівлі не мають звичайної геометричної форми. Це що новий стиль в архітектурі?

-               Гість архітектор: Так. Ви праві. Уже на початку 20 століття архітектура почала змінюватися. Зокрема, з’явилися шедеври біонічного стилю.  

Біоніка – наука про використання в техніці, архітектурі та дизайні знань про конструкцію та форму, принципи та технологічні процеси живої природи. Біоніка в перекладі з грецького означає “той, що живе”. Вивчивши закони, будову і спосіб життя рослин і тварин, архітектори застосовують в інженерних спорудах ті самі принципи. (приклади на слайдах)

-               Скептик: Думаю, що у глядачів виникло запитання де тут присутня математика? 

-               Ведучий: Давайте дізнаємося коментар від експерта доктора наук.

-               Експерт доктор наук: Існує точка зору, що в творіннях природи відсутня геометрія, як проста, так і складна. З цим погодитися неможна. Багато вчених-математиків природні форми намагалися виразити аналітично, тобто за допомогою формул або графіків. Після відкриття Рене Декартом методу координат, вчені отримали новий математичний апарат для дослідження кривих. Сам Декарт винайшов криву, що отримала поетичну назву “Квітка жасмину”. (слайд) Геометричне дослідження природних оболонок.(слайд), моделювання біоформ. (слайд)

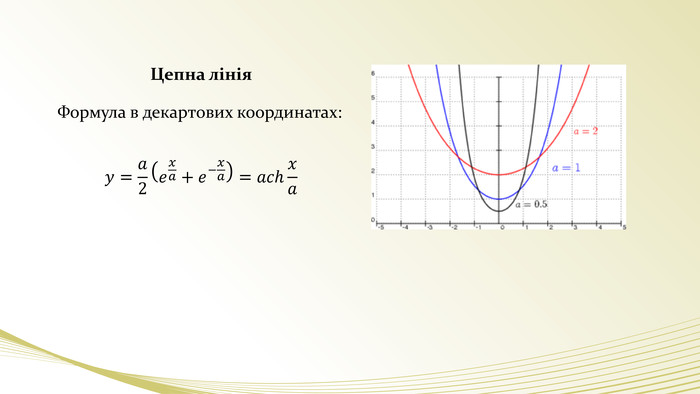
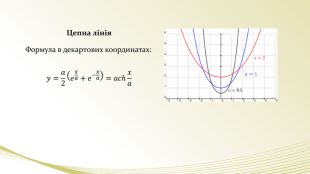
 А ще була винайдена цепна лінія. (слайд)Це крива, форму якої приймає під впливом вантажу гнучка нитка, що не розтягується, якщо кінці її закріпити. Більшість провисаючих природних конструкцій окреслюються цією кривою.

-               Ведучий: А де вона використовується?

-               Доктор наук: Цепна лінія використовується в розрахунках, пов’язаних з провисанням проводів, тросів.  (на мостах) Перевернута цепна лінія – ідеальна форма для арок.(слайд).  На арці в Сент-Луісі написана її формула: (слайд) -  Скептик: А ще можете навести приклади?

-               Експерт доктор наук: Уже говорили про золоту спіраль. “Всюдисуща спіраль” – так часто її характеризують, завдяки її широкому розповсюдженню в природі. Основна властивість - здатність при різних перетвореннях залишатися незмінною. 

-               Скептик: Так. Властивості цієї кривої так вразили Якоба Бернуллі, що він назвав її  “ДИВОВИЖНА СПІРАЛЬ” і   заповів зобразити на своїй могилі з написом “перетворювана, відроджуюся знову”. (слайд)

Ведучий: (слайди) Так.  Якщо придивитися, то в природі така спіраль  виявилася в оболонці молюска, по її дугам розташовані зернята соняшника, молекули ДНК, галактика.

-               Скептик: Цікавий факт: Великий німецький поет Йоганн-Вольфганг Гете вважав спіраль математичним символом життя і духовного розвитку.

-               Ведучий: Нещодавно я натрапила на статтю у журналі “Наука і життя”, що мала назву “Криві, задані в полярних координатах”. У нас в студії є реактор журналу, що детальніше розповість вам про неї.

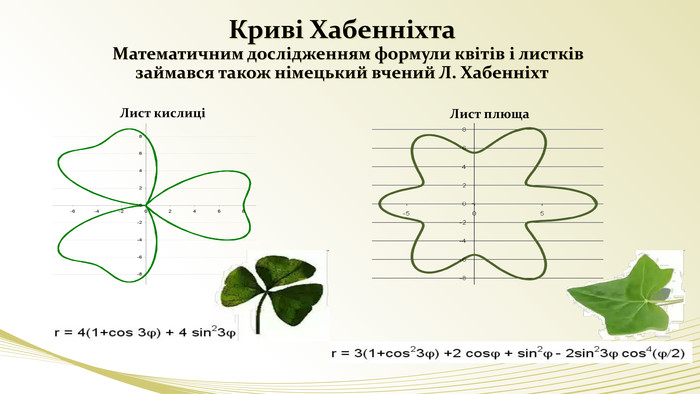
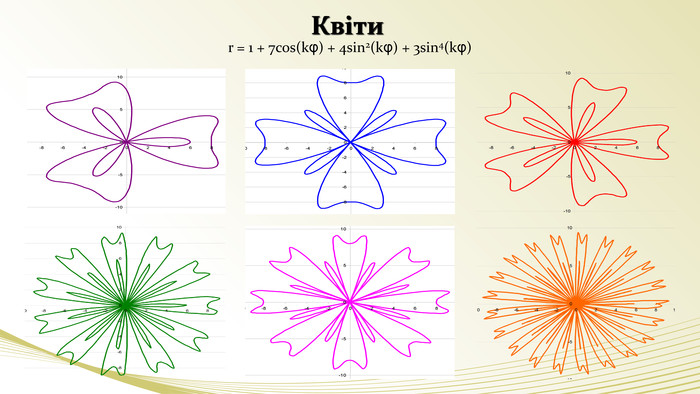
-               Експерт редактор журналу.  Дякую. В 18 столітті італійський геометр Г. Гранді намагався виразити аналітично зовнішні обриси квітів. В математиці сім’я кривих, що досліджував Гранді, отримала назву “Рози”. Але не ті, що ви подумали. (слайди) Ось приклад рівняння кривих, що окреслюють обриси квітів. В рівняння параметр а служить радіусом, а параметр к – кількість пелюсток. Пізніше німецький вчений Хабеніхт винайшов формули листів кислиці та плюща.

-               Скептик: Архівражаюче!  

-               Ведучий: Дякуємо вам, Михайло, за красиву математику.

Фонова музика …

-               Ведучий. Підходить до глядача і запитує:“Скажіть, будь-ласка, Вам відоме слово гіперболоїд?”

-               ???

-               Ведучий. Думаю, що все нам пояснить наш наступний гість. Запрошуємо в студію провідного  будівельника __________________.

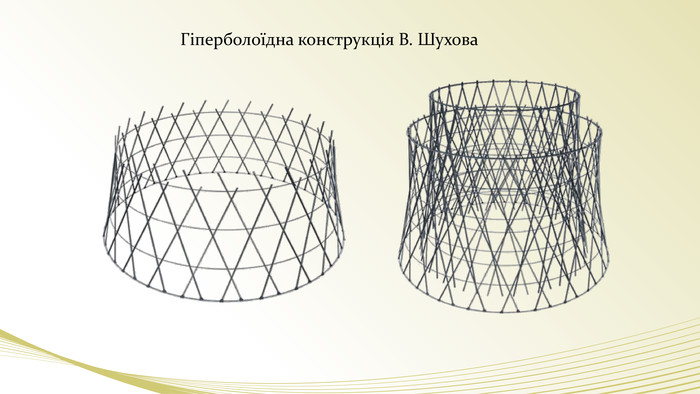
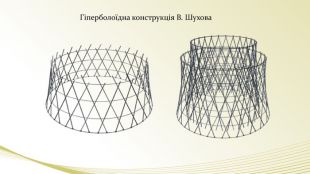
-               Гість будівельник: Я завжди був у захваті від висотних хмарочосів, створених сьогодні. Але мало хто знає, що в основу деяких з них покладено гіперболоїдну форму. Професор і експерти зрозуміють що я маю на увазі. Перед тим, як я покажу вам відеоматеріали таких конструкцій, попрошу надати їм слово. 

-               Ведучий. Справді, таке цікаве слово…. “гіперболоїд”. Що це таке ми запитаємо в професора.

-               Експерт доктор наук: з точки зору математики - це тіло 2-го порядку, що задається рівнянням (показує). Якщо вам в цьому важко розібратися,  я покажу, що у цього тіла є чудові властивості, які дозволять наочно його уявити. (Демонстрація). Така конструкція дуже жорстка і міцна.

-               Скептик: Я знаю, що в журналі “Наука і життя” публікують статті про відомих людей-винахідників. Михайло, ви можете щось сказати на рахунок цього?

-               Експерт редактор журналу: Так, хочу познайомити вас із видатним російським інженером, архітектором, науковцем і винахідником Шуховим. (слайд) Він першим ввів у архітектуру гіперболоїдну форму та розробив  проект гіперболоїдної вежі заввишки 350 метрів. (слайд)Перевершуючи Эйфелеву вежу на 50 метрів по висоті, конструкція російського інженера дозволяла зробити споруду міцнішою і в чотири рази більше легкою! 

-               Ведучий: Вам відомий цей винахідник? (звертається до будівельника)

-               Гість будівельник: Звичайно. По принципу Шухова розпочали будувати водонапірні вежі, морські маяки, радіовежі, опори ліній електропередач, башти на кораблях військового флоту, пожежні та сигнальні вежі. (слайд) Причому усі з радістю говорять, що це Шухов. Це його теорія, його розрахунки. Це буде стояти довго, воно не впаде, з ним нічого не станеться. Давайте переглянемо (слайди):

-               Ведучий: А пам’ятаєте фантастичний роман "Гіперболо́їд інженера

Га́ріна"?  

-               Скептик: Ти думаєш це той самий гіперболоїд?

-               Експерт редактор журналу: Дійсно, на створення цього роману А. Н. Толстого надихнув заворожливий образ конструкції Шуховской вежі. Відомі ще й екранізації:  «Гіперболоїд інженера Гаріна», режиссёр Олександр Гінцбург,  «Крах інженера Гаріна».

-               Скептик: Одне слово, а присутнє в математиці, будівництві, літературі, кінематографії. Архівражаюче!

Фонова музика …

-               Ведучий. Так. Юра, зверни увагу, у  мене в руках така ось стрічка. Мені її прислав у посилці наша глядачка  ______________. І додала такий лист (дістає з коробки і читає): “Шановні ведучі. Поясніть такий парадокс: Чому не можна розмалювати цей лист з обох сторін?” Ну і цікаве запитання. Зустрічайте нашу наступну гостю, для якої заняття математикою стало хоббі – _____________.

-               Скептик:  На перший погляд нічого особливого, звичайна стрічка. (передає гостю).

-               Гість дослідник: Але якщо придивитися уважніше? Над нею можна проводити цікаві експерименти. Хочу показати вам деякий експеримент.

Розріжемо її по середині. Як ви думаєте що вийде?... 

-               Ведучий: ??? напевно дві стрічки.

-               Гість дослідник: (розрізає і показує результат) Вийде ще довша одна стрічка. І це ще не усі експерименти, які можна зробити. Давайте ще раз розріжемо її. Як ви думаєте що вийде? (демонструє) 

-               Ведучий: Ну я тепер уже не знаю. Ти як гадаєш, (звертається до скептика). 

-               Скептик: Не знаю, напевно ще довша стрічка.

-               Гість дослідник: А вийде дві стрічки! Спробуйте і ви виконати такі експерименти! 

-               Скептик:   архівражаюче! 

-               Ведучий. Цікаво. Давайте дізнаємося думку експертів, будь-ласка, редактор журналу.

Експерт редактор журналу: Ця стрічка називається лист Мебіуса. Німецький математики Мебіус узяв стрічку, повернув її кінець на 180º і склеїв з другим кінцем. Чи він це зробив від нудьги, чи від наукового експерименту, але так з’явилася у науці знаменита Стрічка Мебіуса.

-               Скептик:   А чим же вона знаменита? 

-               Експерт доктор наук: А тим, що має лише одну сторону. Це дуже легко перевірити. Візьміть олівець і проведіть пряму,  не відриваючи руки. Ви не зможете перевернути її на іншу сторону, навіть якщо дуже захочете, тому що це одностороння поверхня. Таку цікаву властивість вона має. Тому з обох сторін ви її не розмалюєте.   

-               Ведучий:  У нас є можливість взяти участь у науковому експерименті! А що вийде, якщо стрічку повернути на три оберти і склеїти? (передає глядачу щоб він провів експеримент)

-               Експерт доктор наук: Хочу додати, що такий розділ математики, який займається дослідженням односторонніх поверхонь,  називається топологія. Наука ця настільки важка, що її не вивчають у школах.

-               Гість дослідник:  Але хто його знає, можливо саме ви, глядачі, станете знаменитим топологом і якусь замисловату поверхню назвуть вашим іменем! Експериментуйте!

-               Ведучий:  Нам із ____ відомо, що ви швидко множите, використовуючи при цьому цікавий спосіб.

-               Гість дослідник. Так. Є ще китайське множення, маловідоме, але дуже цікаве. (демонструє)

-               Скептик: Справді, цікава математика.

-               Ведучий: Просимо запитання від експерта.

-               Експерт художник: у знаменитій гравюрі Альбрехта Дюрера зображено такий квадрат із цифрами. (слайд). Що вони означають?  

-               Дослідник: Це, магічний квадрат. Прямокутна таблиця, заповнена числами, що мають цікаві властивості, наприклад сума чисел по горизонталі і вертикалі і по діагоналі дорівнює 34. Перевірте!

-               Скептик: Я перевіряв. На гравюрі це саме так.

-               Ведучий: А чому саме 34?

-               Дослідник: Це число називається магічна константа. Для того, щоб її визначити, є спеціальна формула (демонструє на дошці). Давайте визначимо магічну константу для квадрата четвертого порядку(показує обчислення на дошці) – це число 34. 

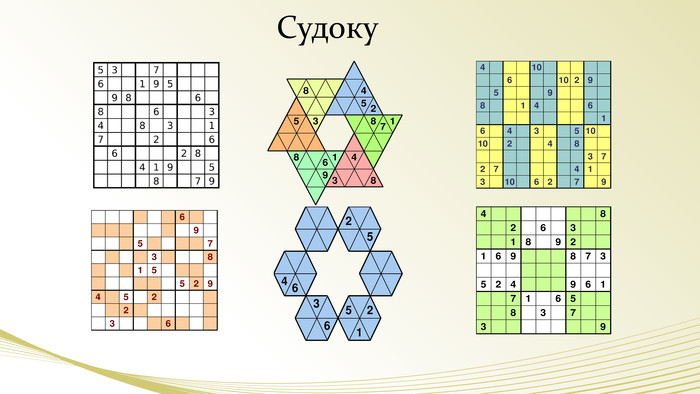
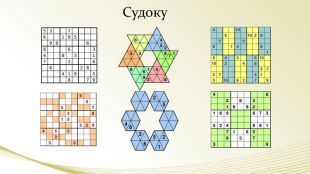
-               Скептик: Можна сказати, що різновидом магічних квадратів є знамениті судоку!

-               Дослідник: Це не зовсім так. Судоку – це так званий латинський квадрат дев’ятого порядку (9 рядків і 9 стовпців). 

-               Скептик: Судоку активно публікують газети , журнали різних країн світу, збірники судоку випускають великими тиражами.

-               Дослідник: Так. Сьогодні це дуже корисна і популярна річ. Вона удосконалює логіку мислення, розвиває уважність. А хочете математичний фокус - я вгадаю ваш вік?

-               Ведучий. Як ви це зробите.

-               Дослідник: За допомогою математики.

-               Ведучий: Спробуйте

-               Дослідник демонструє

-               Ведучий. Дякуємо вам, Вікторія, за цікаву математику. Дійсно,  людина багатогранна. У кожного з нас є якийсь талант від природи. Хтось знає математику, фізику, інформатику, а хтось малює, танцює, співає, складає вірші. Але, як сьогодні ми ще раз переконались, математика є і в науці, і в техніці, і в літературі, і в мистецтві, і в музиці.

-               Скептик: Так, історичне значення математики полягає в тому, вона служила і служить людині, що вона тісно пов’язана з іншими науками, що вона вважає своїм головним призначенням “ знаходити порядок в хаосі, який нас оточує”. Дякуємо усім гостям та експертам нашої програми, до наступних зустрічей. І насамкінець прошу до вашої уваги добірку цікавих і неспіваних фактів. І музичний дарунок.

Заключне слово вчителя