Практична робота 10 клас Тригонометрія. "Обчислення наближених значень тригонометричних функцій за допомогою тригонометричного круга."

Практична робота 10 клас

Тема. Тригонометрія. Обчислення наближених значень тригонометричних функцій за допомогою тригонометричного круга

Мета: навчитися знаходити наближені значення тригонометричних функцій за допомогою тригонометричного круга.

Обладнання: одиничний тригонометричний круг.

Учні повинні знати: означення тригонометричних функцій числового аргументу і кута, формули  зведення, додавання, поняття парністі

(непарності) та періодичності тригонометричних функцій, властивостей функцій у = tgх та у = ctgх.

Хід роботи

Обчислення наближених значень тригонометричних функцій синус і косинус за допомогою тригонометричного круга.

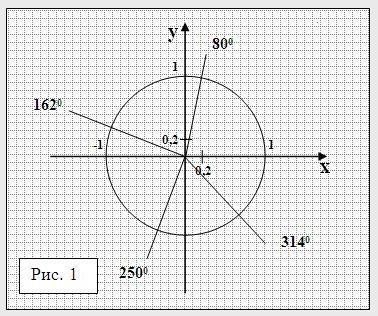
1. Обчислити наближені значення sinα і cosα, користуючись тільки малюнком тригонометричного круга (рис. 1).

1) sin80⁰; 2) sin162⁰;        3) sin250⁰;       4) sin314⁰;

5) cos80⁰;          6) cos162⁰;        7) cos250⁰;       8) cos314⁰;

9) sin100⁰;        10) sin28⁰;        11) sin170⁰;      12) sin344⁰;

13) cos100⁰; 14) cos28⁰;       15) cos170⁰;      16) cos344⁰; 17) sin(-80⁰);    18) sin(-314⁰);   19) sin970⁰; 20) sin(-522⁰);

21) cos(-80⁰);    22) cos(-314⁰); 23) cos970⁰;     24) cos(-522⁰).

 Значення синуса і косинуса кутів в завданнях 1 – 8 знаходять, користуючись означеннями синуса і косинуса на одиничному тригонометричному крузі, а в завданнях 9 – 24 використовують формули зведення, парність (непарність) та періодичність тригонометричних функцій.

Наприклад:

9) sin100⁰=sin(180⁰-80⁰)=sin80⁰;

15) cos170⁰=cos(90⁰+80⁰)=- sin80⁰;

17) sin(-80⁰)= -sin80⁰;

19) sin970⁰=sin(2·360⁰+250⁰)= sin250⁰;

24) cos(-522⁰)= cos522⁰=cos(360⁰+162⁰)= cos162⁰.

2.   Отримані результати занести в таблицю.

Обчислення наближених значень тригонометричних функцій тангенс і котангенс  за допомогою тригонометричного круга.

1.     На тригонометричному крузі нанести лінії тангенса і котангенса.

2.     Обчислити наближені значення tgα і ctgα, користуючись тільки тригонометричним кругом  

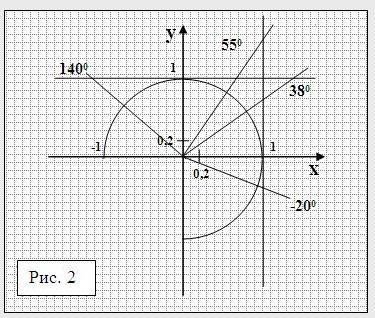
1) tg38⁰;          2) tg55⁰;            3) tg(-20⁰);

4) ctg38⁰;        5) ctg55⁰;          6) ctg140⁰;

7) tg52⁰;          8) ctg35⁰;          9) tg160⁰;

10) ctg500⁰;    11) tg(-410⁰); 12) ctg(-830⁰).

          Завдання 1 – 6 виконують, користуючись означенням тангенса і котангенса числового аргументу.

 Значення тангенса і котангенса в завданнях 7 – 12 знайти, виконуючи перетворення за допомогою формул зведення та властивостей функцій у=tgх та у=ctgх.

         Наприклад:

         7) tg52⁰=tg(90⁰-38⁰)= ctg38⁰;

10)  ctg500⁰=ctg(2·180⁰+140⁰)= ctg140⁰;

11)  tg(-410⁰)=- tg410⁰=-tg(270⁰+140⁰)=-(- ctg140⁰)= ctg140⁰.

3.     Отримані результати занести в таблицю.

Записати висновки.