урок на тему "Розв'язування ірраціональних рівнянь"
Розробка уроку з алгебри у 10 класі на тему: "Розв'язування ірраціональних рівнянь".
Мета уроку: активізація розумової діяльності учнів шляхом використання різних форм і методів роботи; узагальнити і систематизувати знання, уміння і навички учнів з теми «Ірраціональні рівняння"; розвивати пам'ять, увагу, спостережливість, математичне мовлення, загальну обізнаність, вміння оцінювати отриманий результат та аналізувати його .
Тема: Розв’язування ірраціональних рівнянь.
Мета:
методична мета: активізація розумової діяльності учнів шляхом використання різних форм і методів роботи.
навчальна мета: узагальнити і систематизувати знання, уміння і навички учнів з теми «Ірраціональні рівняння».
розвиваюча мета: розвивати пам’ять, увагу, спостережливість, математичне мовлення, загальну обізнаність, вміння оцінювати отриманий результат та аналізувати його .Розвивати вміння застосовувати знання отримані на уроці в ситуаціях повсякденного життя, чітко та зрозуміло висловлювати власну думку, робити грунтовні висновки.
виховна мета: виховувати уважність, ввічливість у спілкуванні з учителем та однокласниками, вміння плідно співпрацювати з однокласниками для досягнення мети, виваженість у своїх твердженнях та цікавість до отримання нових знань.
Тип уроку: узагальнення і систематизація знань, вмінь і навичок.
Обладнання: мультимедійний проектор, картки з завданням.
Форми організації праці: індивідуальна, фронтальна, парами.
Очікувані результати:
у процесі уроку учні зможуть:
- Узагальнити відомості про розв’язування ірраціональних рівнянь;
- Удосконалити свої уміння та навички розв’язування ірраціональних рівнянь;
- Концентруватися та максимально викладатися в обмежений час;
- Всі учні на уроці отримають оцінку.
Структура уроку:
- Організаційний момент.
- Перевірка домашнього завдання.
- Формулювання теми і мети уроку. Мотивація навчальної діяльності.
- Актуалізація знань.
- Узагальнення і систематизація знань.
- Узагальнення і систематизація вмінь.
- Підведення підсумків уроку.
- Рефлесія.
- Домашнє завдання.
Епіграф уроку: Математика вчить мислити й разом з тим вселяє віру в безмежні сили людського розуму. Вона виховує волю, характер.
В.О. Сухомлинський
Хід уроку
- Організаційний момент.
Ми продовжимо нашу співпрацю в опануванні основи більшості наук – математики. А епіграфом нашої роботи будуть слова:(слайд 2)
Для плідної роботи ви повинні бути уважними, тому виконаємо завдання на увагу: (слайд 3)




![]()
![]()
-Які фігури зображені ?
- Якого кольору?
- Що зображено в трикутнику, в колі, в квадраті?
- Перевірка домашнього завдання. (слайд 4)+
№481
- Відповідь : 4
- Відповідь : 2;3
- Відповідь : -7;8
- Відповідь : -1;1;4.
- Мотивація навчальної діяльності.
Люди у своїй роботі часто оперують рівняннями, тобто рівностями , у яких знаючи певну кількість відомих величин і їх взаємозв’язок можна знайти невідому величину, що залежить від даних. Рівняння – це чудовий інструмент, за допомогою якого, можна задачу перетворити в красиве, струнке речення. Причому багато задач, різноманітних за змістом і з різних галузей діяльності людини зводяться до рівняння певного типу, яке служить знаковою моделлю цієї групи задач. Уміння розв’язати певний тип рівнянь дає можливість розв’язати цілу групу задач. Метод рівнянь – один з математичних методів пізнання реальної дійсності.
Які види рівнянь ви знаєте? На попередніх уроках ми познайомились з ірраціональними рівняннями. Виявляється ірраціональні ріняння застосовуються не лише в математиці, але і в фігурному катанні, біології, фізиці, авіації.(слайд6) Мета нашого уроку узагальнити і систематизувати знання з теми. Але постає питання для чого це нам потрібно? Ірраціональні рівняння є відображенням світу, що нас оточує. Отже ми розуміємо актуальність того над чим працюємо: для виконання завдань зно, для продовження навчання та вивчення інших наук. Оскільки ця тема вивчається не перший урок, звернемося до нашого досвіду, відтворимо знання, щоб скористатися ними в подальшій роботі.
-
Актуалізація опорних знань.
У кожного з вас на столі картки роботи на уроці, і верхня таблиця це оцінка вашої діяльності на уроці, де ви повинні виставляти кількість балів за кожний вид роботи.
Завдання 1.Поняття ірраціональності асоціюється завжди із зображенням кореня. Знак кореня з’явився в 1525 році. До нашого часу його зображення змінювалось. Хто вперше ввів це зображення? Про це ви дізнаєтесь, розгадавши кросворд (слайд 7).
Запитання:
- Як називається рівняння, в якому змінна знаходиться під знаком кореня? (ірраціональне)
- Як називають корінь третього степеня? (кубічний)
- При піднесенні рівняння до парного степеня отримаємо рівняння … (наслідок)
- Як називається корінь рівняння, який одержуємо в результаті нерівносильних перетворень і який не задовольняє умову рівняння?? (сторонній).
- При піднесенні рівняння до непарного степеня, то отримаємо рівняння … даному (рівносильне)
-
Корінь рівняння
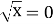 (нуль)
(нуль)
- Якщо кожному значенню змінної х з деякої множини відповідає єдине значення змінної у, то таку залежність називають…( функцією)
|
|
1 |
і |
Р |
р |
а |
ц |
і |
о |
н |
а |
л |
ь |
н |
е |
|||||
|
2 |
к |
У |
б |
і |
ч |
н |
и |
й |
|
||||||||||
|
|
|
3 |
н |
а |
с |
л |
і |
Д |
о |
к |
|
||||||||
|
|
|
4 |
с |
т |
О |
р |
о |
н |
н |
і |
й |
||||||||
|
5 |
р |
і |
в |
н |
о |
с |
и |
Л |
ь |
н |
е |
||||||||
|
|
6 |
н |
у |
л |
Ь |
|
|||||||||||||
|
|
7 |
Ф |
у |
н |
к |
ц |
і |
є |
ю |
||||||||||
Отримане слово Рудольф (Крістоф Рудольф) приносить вам 2 бали.(слайд 8)
5.Узагальнення і систематизація знань.
Завдання 2. (усні відповіді) (слайд 9)
Знайдіть серед запропонованих рівнянь ірраціональні рівняння:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
Завдання 3.(усні відповіді) (слайд 10)
Чи являється число коренем рівняння:
6.Узагальнення і систематизація вмінь .
Завдання 4.(лото) (6 балів) (слайд 11)
|
-32 |
9 |
0 |
121 |
Рівняння коренів не має |
64 |
|
а |
д |
к |
е |
т |
р |
Розв’язати рівняння:
-
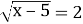 (4)
(4)
-
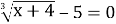 (121)
(121)
-
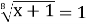 (0)
(0)
-
 (-32)
(-32)
-
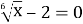 (64)
(64)
-
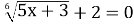
ІІ варіант
|
5 |
4 |
-3 |
-125 |
Рівняння коренів не має |
-5 |
|
ю |
а |
н |
0 |
ь |
т |
Розв’язати рівняння:
-
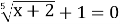
-
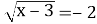
-
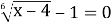
-
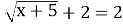
-
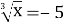
-
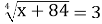
(Риска над підкореневим виразом спочатку була відсутня; її пізніше ввів Рене Декарт. Звичне нам позначення кореня довільного степеня почав використовувати Альбер Жирар (1629). Закріпився цей формат завдяки Ньютону та Лейбніцу. )
Ми повторили означення ірраціонального рівняння, коренів рівняння, властивості кореня n-го степеня та розв’язування найпростіших ірраціональних рівнянь.Тепер давайте пригадаємо методи розв’язування ірраціональних рівнянь.(слайд 12)
Завдання 5. (4 бали) (слайд 13)
Поставити у відповідність записаному рівнянню номер метода , який застосовується для його розв’язання:
Методи:
- Піднесення до степеня;
- Заміні змінної;
- Розкладання на множники;
-
Використання властивостей функції у=
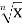
Варіант 1
|
Рівняння |
Методи розв’язування |
|||
|
|
1 |
2 |
3 |
4 |
|
1) |
|
|
|
|
|
2) |
|
|
|
|
|
3) |
|
|
|
|
|
4) |
|
|
|
|
Варіант 2
|
Рівняння |
Методи розв’язування |
|||
|
|
1 |
2 |
3 |
4 |
|
1) |
|
|
|
|
|
2) |
|
|
|
|
|
3) |
|
|
|
|
|
4) (х+3) |
|
|
|
|
Відповіді (слайд 11)
Варіант І Варіант 2
|
|
1 |
2 |
3 |
4 |
|
1 |
|
+ |
|
|
|
2 |
|
|
+ |
|
|
3 |
+ |
|
|
|
|
4 |
|
|
|
+ |
|
|
1 |
2 |
3 |
4 |
|
1 |
+ |
|
|
|
|
2 |
|
+ |
|
|
|
3 |
|
|
|
+ |
|
4 |
|
|
+ |
|
Ми прийшли до висновку, що при розв’язуванні будь-якого ірраціонального рівняння треба застосовувати метод «пильного погляду», тобто спочатку треба уважно роздивитись і проаналізувати умову рівняння, а потім уже визначатись з методом розв’язання.
Завдання 6. Поясніть хід розв’язування ірраціонального рівняння: (слайд 14
1)![]() 2)
2) ![]()
Завдання 7. Скільки коренів має рівняння: (слайд 15)
![]()
Завдання 8. (робота в парі) (слайд 16)
Виконати задання, 2 бала отримує пара, яка правильно справилася з завданням
№1 Знайти суму коренів рівнянь (В: 6)
1) Розв’яжіть рівняння ![]() = х-1 (В: 7)
= х-1 (В: 7)
2) Розв’яжіть рівняння (х+1)![]() (В: -3;2)
(В: -3;2)
№2 Знайти добуток коренів рівнянь (В :0)
1) Розв’яжіть рівняння ![]() ( В : 3)
( В : 3)
2) Розв’яжіть рівняння ![]() (В: 0)
(В: 0)
№3 Знайти середнє арифметичне коренів рівняння (В:-![]() )
)
-
Розв’яжіть рівняння
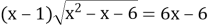 (В:7; -6)
(В:7; -6)
-
Розв’яжіть рівняння
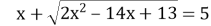 (В :-2)
(В :-2)
Одна з пар виконує завдання на відкидній дошці
7.Підведення підсумків уроку. (слайд 17)
Підраховуємо бали і переводимо в оцінку.
8.Рефлексія (слайд 17)
У вас на столі лежать різнокольорові геометричні фігури, з яких ми почали наш урок .
- Хто не допустив жодної помилки і повністю задоволений результатом, оберіть собі фігуру червоного кольору.
- Хто допустив неточність – жовтого кольору
-
А кому треба ще постаратися і успіх обов’язково прийде – синього кольору.
Я вважаю , що всі успішно попрацювали .
9.Домашнє завдання (слайд 18)

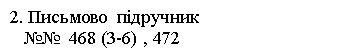
(Прізвище, ім’я) Варіант 1
|
Вид роботи |
Кросворд |
Лото |
Відповідність (максим 4 б.) |
Робота в парі (максим. 2б.) |
Усні відповіді |
|
|
К-сть балів |
|
|
|
|
|
Всього ОЦІНКА |
1.Кросворд
Запитання:
1. Як називається рівняння, в якому змінна знаходиться під знаком кореня?
2.Як називають корінь третього степеня?
3.При піднесенні рівняння до парного степеня отримаємо рівняння …
4. Як називається корінь рівняння, який одержуємо в результаті нерівносильних перетворень і який не задовольняє умову рівняння?
5.При піднесенні рівняння до непарного степеня, то отримаємо рівняння … даному
6.Корінь рівняння ![]()
7.Якщо кожному значенню змінної х з деякої множини відповідає єдине значення змінної у, то таку залежність називають…
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|||||||||
|
5 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
6 |
|
|
|
|
|
|||||||||||||
|
|
7 |
|
|
|
|
|
|
|
|
||||||||||
|
-32 |
9 |
0 |
121 |
Рівняння коренів не має |
64 |
|
а |
д |
к |
е |
т |
р |
2. Лото
Розв’язати рівняння:
1)![]() 2)
2) ![]() 3)
3) ![]()
4) ![]() 5)
5) ![]() 6)
6) ![]()
|
Рівняння |
Методи розв’язування |
|||
|
|
1 |
2 |
3 |
4 |
|
1) |
|
|
|
|
|
2) |
|
|
|
|
|
3) |
|
|
|
|
|
4) |
|
|
|
|
3.Відповідність.
4.Робота в парі
(Прізвище, ім’я) Варіант 2
|
Вид роботи |
Кросворд |
Лото |
Відповідність (максим 4 б.) |
Робота в парі (максим. 2б.) |
Усні відповіді |
|
|
К-сть балів |
|
|
|
|
|
Всього ОЦІНКА |
1.Кросворд
Запитання:
1. Як називається рівняння, в якому змінна знаходиться під знаком кореня?
2.Як називають корінь третього степеня?
3.При піднесенні рівняння до парного степеня отримаємо рівняння …
4.Як називається корінь рівняння, який одержуємо в результаті нерівносильних перетворень і який не задовольняє умову рівняння?
5.При піднесенні рівняння до непарного степеня, то отримаємо рівняння … даному
6.Корінь рівняння ![]()
7.Якщо кожному значенню змінної х з деякої множини відповідає єдине значення змінної у, то таку залежність називають…
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|||||||||
|
5 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
6 |
|
|
|
|
|
|||||||||||||
|
|
7 |
|
|
|
|
|
|
|
|
||||||||||
|
5 |
4 |
-3 |
-125 |
Рівняння коренів не має |
-5 |
|
ю |
а |
н |
0 |
ь |
т |
2. Лото
Розв’язати рівняння:
-
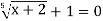 2)
2)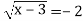 3)
3)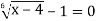
4)![]() 5)
5)![]() 6)
6)![]()
|
Рівняння |
Методи розв’язування |
|||
|
|
1 |
2 |
3 |
4 |
|
1) |
|
|
|
|
|
2) |
|
|
|
|
|
3) |
|
|
|
|
|
4) (х+3) |
|
|
|
|
3.Відповідність.
4.Робота в парі.
№1 Знайти суму коренів рівнянь
1) Розв’яжіть рівняння ![]() = х-1
= х-1
2) Розв’яжіть рівняння (х+1)![]()
№2 Знайти добуток коренів рівнянь
1) Розв’яжіть рівняння ![]()
2) Розв’яжіть рівняння ![]()
№3 Знайти середнє арифметичне коренів рівняння
-
Розв’яжіть рівняння
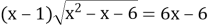
-
Розв’яжіть рівняння
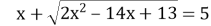
№1 Знайти суму коренів рівнянь
1) Розв’яжіть рівняння ![]() = х-1
= х-1
2) Розв’яжіть рівняння (х+1)![]()
№2 Знайти добуток коренів рівнянь
1) Розв’яжіть рівняння ![]()
2) Розв’яжіть рівняння ![]()
№1 Знайти суму коренів рівнянь
1) Розв’яжіть рівняння ![]() = х-1
= х-1
2) Розв’яжіть рівняння (х+1)![]()
№2 Знайти добуток коренів рівнянь
1) Розв’яжіть рівняння ![]()
2) Розв’яжіть рівняння ![]()


про публікацію авторської розробки
Додати розробку
