УРОК

Тема уроку: Графіки функцій.

Мета уроку: Повторити загальний вигляд графіків деяких видів функцій. Формування умінь будувати графіки функцій за допомогою восьми базових перетворень графіка функції.

Хід уроку

І. Організаційний етап.

Перевірка готовності учнів до уроку, налаштування на роботу.

ІІ. Перевірка домашнього завдання.

1.      Перевірка завдання, заданого за підручником

2. Математичний диктант.

Закінчіть математичні твердження.

1) Областю визначення функції у = є ...

2) Областю визначення функції у = є ...

3) Областю значень функції у = х² +1 є ...

4) Якщо для функції у = f(x) виконується рівність f(-x) = f(x) для всіх х D(f), то функція ...

5) Графік непарної функції симетричний відносно..­

6) Якщо для будь-яких значень х₁ і х₂ з області визначення функції у = f(x) за умови х₁ < х₂ випливає, що у₁ < у₂ то функція ...

Відповідь:

1) (-;l) (l;+); 2) [1;+); 3) [1;+);

4) парна; 5) початку координат; 6) зростаюча.

IIІ. Актуалізація опорних знань.

Бліцопитування

Встановіть відповідність між функцією та її графіком.

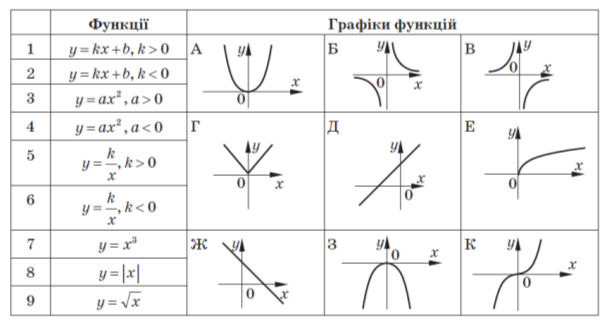
ІV. Повторення і розширення відомостей про графік функції.

1.      Означення графіка функції.

Графіком функції називають множину всіх точок координатної площини, абсциси яких дорівнюють значенням аргументу, а ординати – відповідним їм значенням функції.

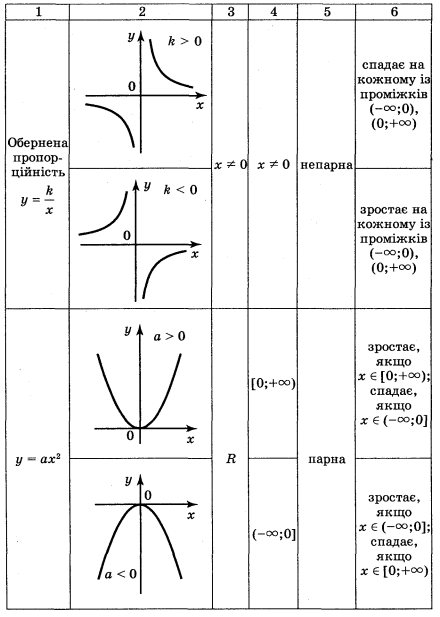
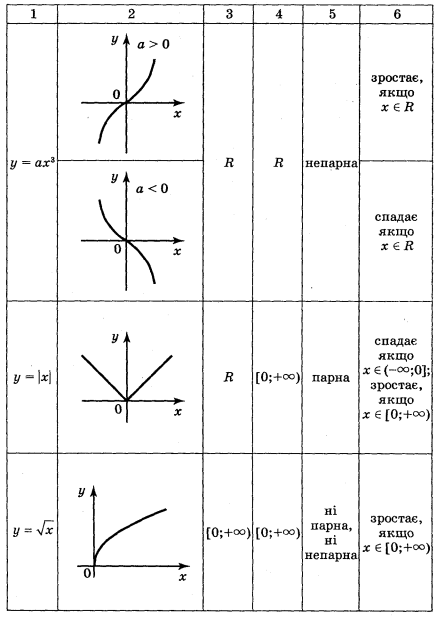
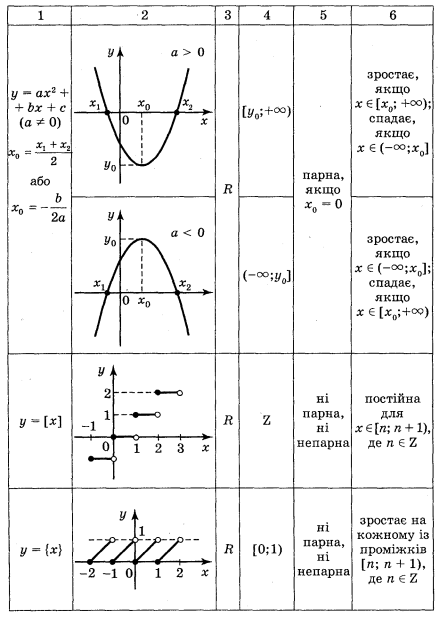
Повторення і узагальнення властивостей вивчених видів функцій провести шляхом фронтальної бесіди і результати зане­сти в Таблицю 1.

2.      Умова, за якої множина точок координатної площини є графіком функції.

Не кожна множина точок координатної площини є графіком деякої функції. Для того, щоб множина точок координатної площини була графіком деякої функції, необхідно, щоб будь-яка пряма, паралельна осі Оу, перетиналась з указаним графіком не більше ніж в одній точці.

Виконання вправи

Які із ліній, зображених на рисунку, є графіком функції? Чому?

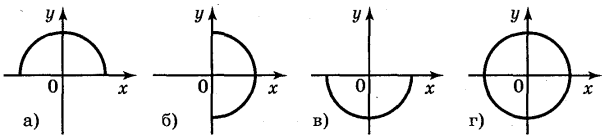
Відповідь: а); в).        

3. Перетворення графіків функцій

  у = f(x): у = -f(x);    у = f(-x); у = f(x) + b; у = f(x + a);

 у = af(x); у = f(ax); у = f(│x│);   у = │f(x)│.

Запас функцій, графіки яких ви вмієте будувати, поки неве­ликий. Але використовуючи відомі із курсів геометрії і алгебри відомості про перетворення фігур, цей список можна суттєво розширити. Згадаємо елементарні перетворення графіка функції у = f(x) за допомогою таблиці 2.

Виконання вправи

Побудуйте графіки функцій

а) у = х - 2;      б) у = 3 - х;     в) у = х² - 2х;    г) у = х² – 4х + 3

Відповідь:

V. Засвоєння знань і умінь.

1. Робота з підручником §1, п.3.

Усно: №1.7.

Письмово:  Середній рівень: №1.8.

   Достатній рівень: №1.16.

   Високий рівень: №1.29, №1.33.

2. Додаткові завдання

1. Побудуйте графік якої-небудь функції f, для якої:

   1) D(f)=[-2;4]; E(f)=[-3;3]; 2) D(f)=(-5;3); E(f)=[2;6];

 3) D(f)=(0;9); E(f)=[-1;5]; 4) D(f)=[-5;0]; E(f)=(1;5).

2. Побудуйте графік функції:

1) ;   2) ; 3) ;    4) ;

5)

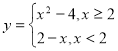
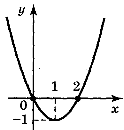
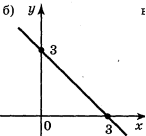
3. Задайте аналітично функцію, графік якої зображено на рисунку:

VІ. Підведення підсумків уроку.

VІІ. Домашнє завдання.

Опрацювати Розділ І § 1 п. 3.

Переглянути відеоролик https://www.youtube.com/watch?v=N6zTRBS0r_g

Виконати письмово:  Середній рівень: №1.9.

    Достатній рівень: №1.17.

    Високий рівень: №1.30, №1.34.

Таблиця 1

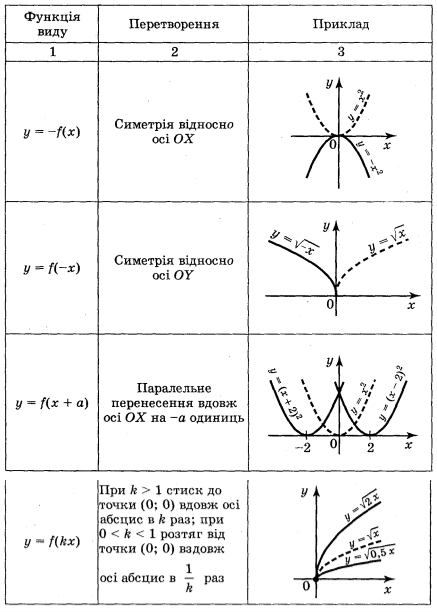
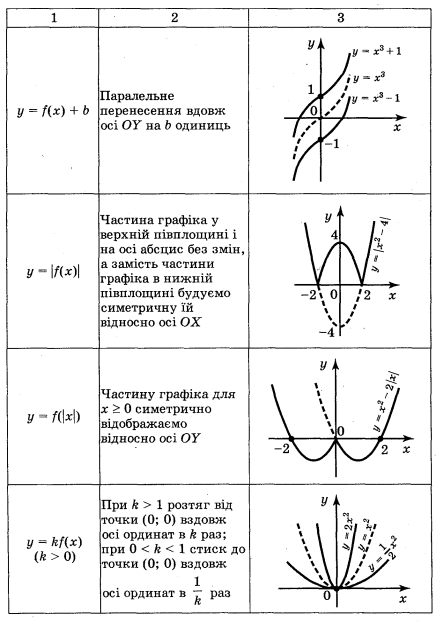Таблиця 2