Практичне заняття "Многогранники"

 Відкрите заняття з математики

                                                                                                                 Викладач Васильків Н.О.

Група 2ДЗ1

Дата: 16 листопада 2021 року

Тема дисципліни: Многогранники.

Тема заняття: Розв’язування задач  на знаходження елементів та площ поверхонь многогранників: призми, паралелепіпеда, піраміди.

Тип заняття: практичне заняття з елементами творчої, пошукової та дослідницької діяльності.

Мета заняття:  набути практичну компетентність, яка передбачає вміння класифікувати і конструювати геометричні фігури в просторі, встановлювати їх властивості, зображати просторові фігури та їх елементи, виконувати побудови на зображеннях, вміння вимірювати геометричні величини на площині й у просторі (відстані, кути), знаходити кількісні характеристики фігур; узагальнити й систематизувати  поняття призми, паралелепіпеда, піраміди; навчитися застосовувати формули для обчислення площі їх бічної поверхні, повної поверхні; формувати просторову уяву; розвивати бажання пізнавати нове, прививати інтерес до математики;  сформувати уміння  використовувати набуті знання, вміння та навички під час розв’язування прикладних  задач.

Студенти повинні:

знати: означення многогранника, призми, паралелепіпеда, піраміди, їх різновиди, формули для обчислення  площі бічної та повної поверхонь призми, паралелепіпеда, піраміди.

вміти: застосовувати набуті знання до розв’язування завдань різного рівня складності.

Міждисциплінарні зв’язки:

Забезпечуючі: математика, інформатика.

Забезпечувані: макетування та робота в матеріалі, композиційна організація форми, основи формоутворення та конструювання, основи креслення і нарисної геометрії.

Забезпечення заняття:

Роздатковий матеріал: таблиця з формулами, картки із завданнями.

Наочність: моделі многогранників, опорні конспекти з теми, слайди, підготовлені студентами.

Технічні засоби навчання: мультимедійний проектор.

Література

Базова:  Істер В.О. Математика: Рівень стандарту: підруч. для 11 класу загальноосвіт. навч. закладів. /  К.,: Генеза -    2019.  Стор. 173-179, 185-189, 195-200.

Допоміжна: 1) Бевз Г.П. Математика: 11 кл.: підруч. для  загальноосвіт. навч. закл. : рівень стандарту /  Г.П.Бевз,
                          В.Г.Бевз. - К.: Генеза -  2011.
                      2) Погорєлов О.В. Геометрія: Стереометрія: підруч. для 10-11 кл. серед. шк. – 6-те вид./ О.В.Погорєлов. –
                          К.: Школяр, 2012.
                      3) Швець В.О. Прикладна спрямованість шкільного курсу стереометрії / Василь Швець, Алла Прус //
                          Математика в школі 2014. - №4. – С.17-24. 

«Теорія без практики  мертва

                                                                                                                                                       і безплідна, практика без

                                                                                                                                                     теорії не можлива»

                                                                                                                                                                                  (Рене Декарт)

Теоретичні відомості

Многогранником називається геометричне тіло, поверхня якого складається зі скінченної кількості многокутників.

Призмою називається  многогранник, у якого дві грані – рівні  n-кутники, а решта n граней – паралелограми.

Призма називається прямою, якщо її бічні ребра перпендикулярні до площини основи. Усі інші призми – похилі. Кожна бічна грань прямої призми – прямокутник.

Висотою призми називається відстань між площинами її основ.

Площина, що проходить через  два бічних ребра призми, які не лежать в одній грані, називається діагональною площиною, а переріз призми цією площиною – діагональним перерізом.

Паралелепіпедом називається призма, в основі якої – паралелограм. Усі грані паралелепіпеда – паралелограми.

Паралелепіпед, бічні ребра якого  перпендикулярні  до площини основи, називається прямим паралелепіпедом. Його бічні грані – прямокутники.

Прямий паралелепіпед,  у якого основою є прямокутник, називається прямокутним паралелепіпедом.

Прямокутний паралелепіпед, в якого всі  ребра рівні, називається кубом.

У прямокутному паралелепіпеді квадрат будь-якої його діагоналі  дорівнює сумі квадратів трьох його лінійних  вимірів:

Пірамідою називають многогранник, одна грань якого – довільний многокутник, а інші грані – трикутники, що мають спільну вершину.

Піраміда називається правильною, якщо її основа – правильний многокутник, а його центр збігається з основою висоти піраміди. Усі бічні ребра правильної піраміди рівні, всі бічні грані -  рівні рівнобедрені трикутники.

Частина піраміди, що міститься між її основою і січною площиною, паралельною основі, називається зрізаною пірамідою. Зрізану піраміду називають правильною, якщо вона є частиною правильної піраміди.

Площі поверхонь

Примітка:   

  кут – виміри прямокутного паралелепіпеда.

Хід заняття

1. Організація студентів до заняття. ( 1 хв)
2. Перевірка домашнього завдання  ( 2 хв). (Консультанти перевіряють належність домашнього завдання).

Підручник (див. базова література), задачі №№ 3.8, 3.12, 3.18, 3.34 (ст.201, 202, 203).

3. Повідомлення теми і мети заняття. (1 хв)

«Ті,  хто полюбляє практику без теорії, подібний  до мореплавця, який  зайшов  на корабель без руля і компаса і тому  ніколи не знає, куди він пливе» (Леонардо да Вінчі)

4. Актуалізація опорних знань.  (10 хв)

• Серед представлених многогранників вкажіть такий, який має 4 грані (тетраедр).
• Покажіть многогранник, який має 5 граней і 6 вершин (трикутна призма).
• Вкажіть многогранники, в  яких  дві основи паралельні  і рівні многокутники, а решта граней – паралелограми (пряма або похила призма).
• Назвіть многогранник, в якого число граней і вершин однакові ( трикутна піраміда).
• Як знайти площу бічної поверхні прямої призми? (треба периметр основи помножити на висоту призми).
• За якою формулою обчислюється площа повної поверхні похилої призми? (
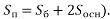
• Як обчислити площу повної поверхні куба з ребром 5 см? (6*5*5=150 см кв.)
• Який многогранник називається пірамідою? (Пірамідою називають многогранник, одна грань якого – довільний многокутник, а інші грані – трикутники, що мають спільну вершину).
• Що таке апофема? (це висота бічної грані піраміди).
• Яка піраміда називається зрізаною? (Частина піраміди, що міститься між  її основою та січною площиною, паралельною основі, називається зрізаною пірамідою).
• Завдання: хто швидше складе запропоновану модель многогранника з магнітного конструктора.

5. Захист проєктів. (26 хв)

Працюючи над проектом «Правильні многогранники», група дослідників отримала завдання виготовити модель одного з многогранників, підготувати презентацію і знайти відповіді на такі питання:

• Скільки є видів правильних многогранників?
• Чому отримали таку назву?
• Які властивості мають?
• Які многокутники є гранями тіла?
• Який вигляд має розгортка правильного многогранника?
• В роботах яких відомих митців зустрічаються правильні многогранники?
• Чи можна в природі та побуті зустріти такі многогранники?

Про результати пошукової роботи ми сьогодні дізнаємось (звіт груп з використанням виготовлених моделей і показом слайдів).

Підведення підсумку етапу захисту проєктів. 

6. Робота в групах. (34 хв)

Студенти діляться на 5 команд. В кожній команді обирають капітана (керівника фірми), конструктора,  фінансиста, маркетолога і дизайнера. Капітан координує і контролює роботу всіх членів команди. Конструктор відповідає за розробку креслення (просторовий  і планіметричний малюнок). Фінансист має правильно застосувати формули та виконати розрахунки. Маркетолог має дати пропозиції щодо втілення проекту (задачі) в життя. Дизайнер відповідає за правильне  естетичне оформлення малюнку .

   Кожна команда отримує по  три задачі різного рівня складності.

7.  Підсумок  заняття ( 2 хв)

Сьогодні  ми повторили означення, основні властивості геометричних тіл та формули для обчислення площ поверхонь призми, паралелепіпеда та піраміди. Застосовували ці знання  при розв’язуванні задач з прикладним змістом. І як підсумок до заняття  хочу нагадати  слова Рене Декарта: «Теорія без практики мертва і безплідна, практика без теорії не можлива»

Оголошення оцінок. Привітання та нагородження кращої команди.

Рефлексія (3 хв)

Студенти  по колу висловлюються одним реченням, обираючи початок фрази з рефлексивного ряду на слайді.

- сьогодні я дізнався …;

- було складно…;

- я виконував завдання…;

- я зрозумів, що…;

- тепер я можу…;

- заняття  дало  мені для життя…;

- мені захотілося….

8. Домашнє завдання (1 хв): підготуватися до контрольної роботи, виконати завдання  №№ 1 – 10 для перевірки знань   з теми: «Многогранники» на стор.214 підручника (див. базова література).