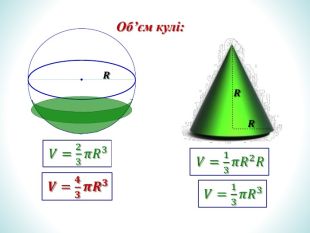
Презентація на тему "Об'єм кулі та її частин".
Про матеріал
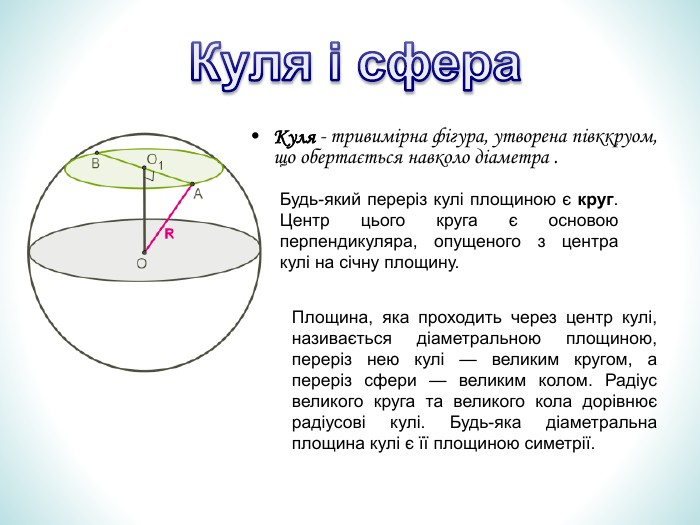
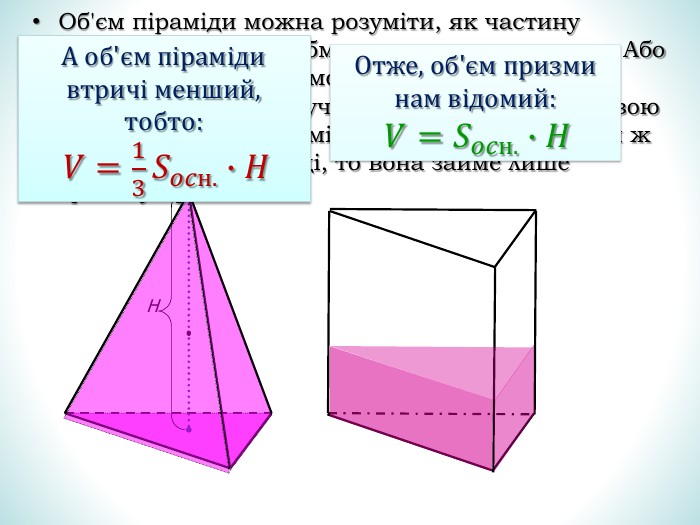
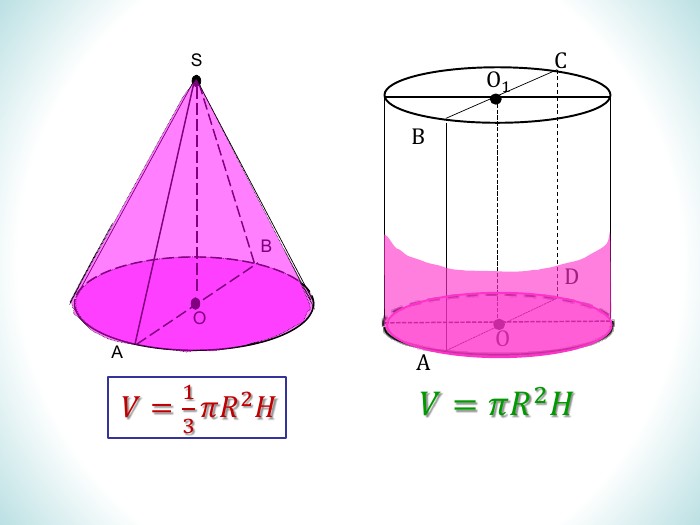
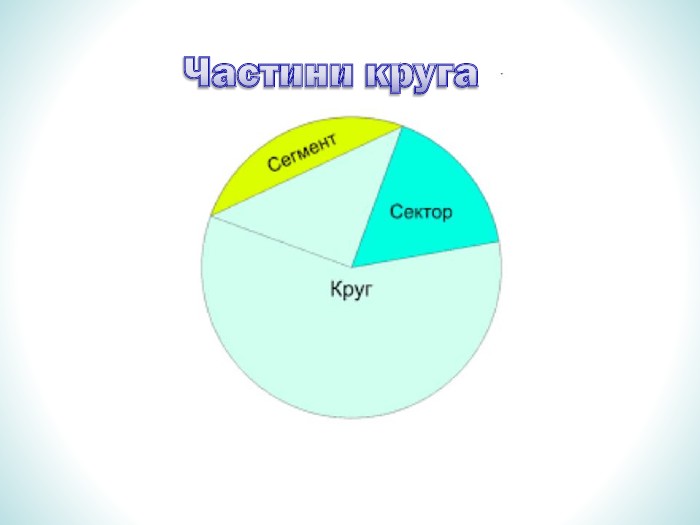
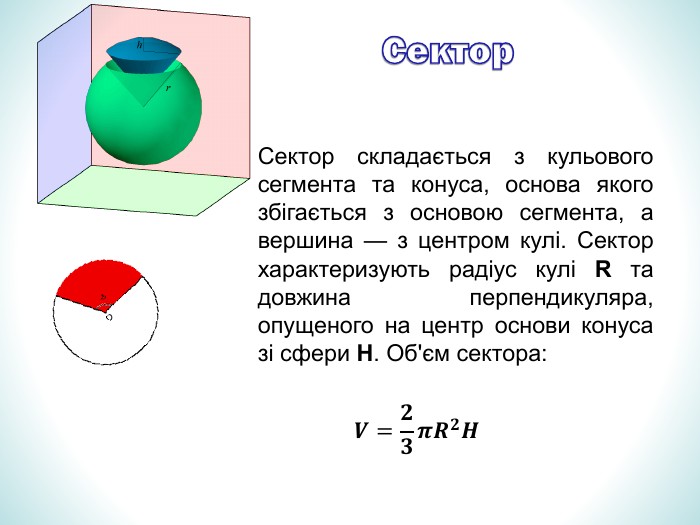
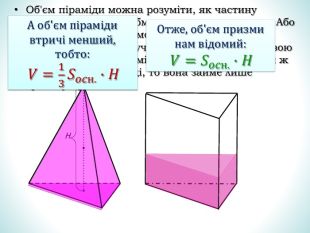
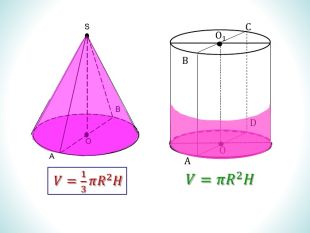
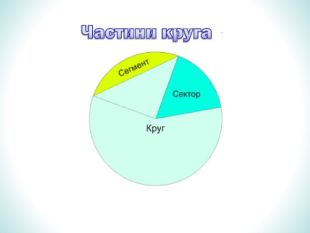
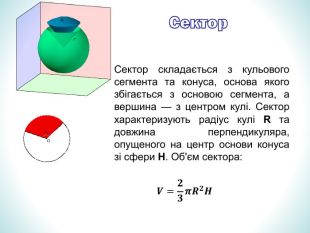
Презентація дає означення кульового сектора та кульового сегмента, їх зображення. За допомогою анімації демонструє співвідношення між об'ємами призми та піраміди, циліндра та конуса з однаковими вимірами. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку