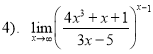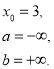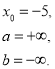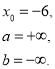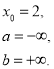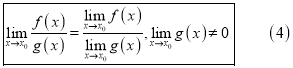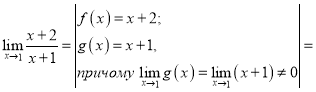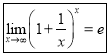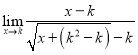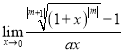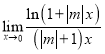Практичне заняття

Тема: Обчислення границь. Дослідження функції на неперервність, визначення точок розриву та асимптот.

Мета: набуття практичних навичок при:

•     Обчисленні границь з використанням основних теорем та правил позбавлення невизначеностей;
•     Дослідженні функції на неперервність;
•     Встановленні типів точок розриву;
•     Дослідженні асимптот та їх побудови.

Робоче місце – учбове місце в кабінеті;

Тривалість заняття – 90 хв;

Обладнання  та наочність: інструкція до виконання практичного заняття №10.

Хід заняття:

І. Організаційні моменти.

ІІ. Вхідний контроль.

Тестування:

Визначити тип невизначеності.
А		Б	В		Г
2. Встановити відповідність між границями та значеннями
А		Б	В		Г
3. Функція в точці має розрив ІІ роду. Причому відомо, що . Схематично зобразити, як поводить себе функція в околі точки , якщо
Варіант 1	Варіант 2		Варіант 3	Варіант 4

ІІІ. Основні поняття.

ОСНОВНІ ТЕОРЕМИ ПРО ГРАНИЦІ ФУНКЦІЇ

	.

Розкриття невизначеностей

Невизначеність виду - задана відношенням двох многочленів Правило: потрібно чисельник і знаменник розділити на найвищий степінь у цих многочленах.
Висновки:
Вигляд відношення	Значення границі
Степінь чисельника дорівнює степені знаменника	Відношенню коефіцієнтів при старших степенях
Степінь чисельника менше степені знаменника
Степінь чисельника більше степені знаменника
Невизначеність виду - задана відношенням двох многочленів Означення: Множник через який чисельник і знаменник прямують до нуля називається критичним множником. Правило:  Потрібно у чисельнику і знаменнику, заданого відношення, виділити критичний множник і скоротити на нього дріб. Якщо при цьому розкладання на множники виявиться утрудненим, то треба розділити чисельник і знаменник на критичний множник  «у стовпчик».
Невизначеність виду - задана ірраціональними виразами.   Правило: крок 1 – позбутися ірраціональності в чисельнику ( помножити на спряжене до чисельника чисельник і знаменник; шляхом введення нової змінної); крок 2 - скоротити на критичний множник .
Невизначеність виду - задана ірраціональними виразами   Правило: Невизначеність виду шляхом рівносильних перетворень потрібно звести до невизначеності ,яку позбавитись за вище описаним алгоритмом.

 Важливі границі

І важлива границя		Наслідки

ІІ важлива границя		Наслідки

Алгоритм дослідження функції на неперервність

Обчислити значення функції в точці х0; Обчислити границю функції при ; Перевірити виконання рівності: (значення функції в точці х0 співпадає з границею функції в т.х0)

Класифікація точок розриву

Асимптоти

Означення: Пряма називається асимптотою кривої, якщо відстань від змінної точки М кривої до цієї прямої при віддаленні точки М у нескінченність прямує до нуля.

Асимптоти
Вертикальні	Похилі
Якщо або то пряма є вертикальною асимптотою для графіка функції Зауваження: якщо функція дробового виду то її обов’язково потрібно обстежити на наявність вертикальних асимптот в точках при яких знаменник обертається в нуль.	Рівняння дотичної в загальному вигляді , тоді Зауваження: якщо хоча б одна з границь не існує, то крива похилих асимптот у відповідній півплощині не має.

 

IV. Систематизація та узагальнення знань студентів.

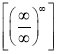
Приклад 1.1: Визначити тип невизначеності та знайти границі:

;  ;

Розв'язання

.

ІІ спосіб:  

.

.

.

.

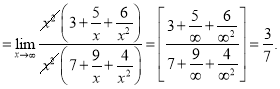
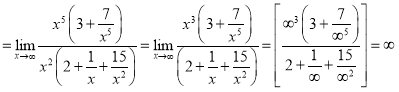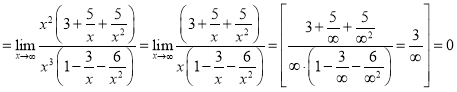Приклад 1.2 Визначити тип невизначеності та знайти границі:

;

Розв’язання

.

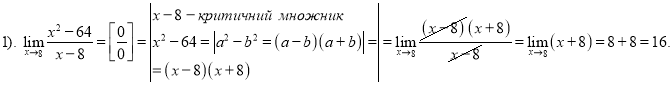
Приклад 1.3 Визначити тип невизначеності та знайти границі:

;  .

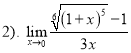Розв’язання

.

.

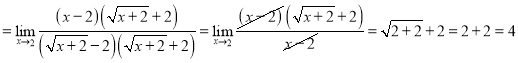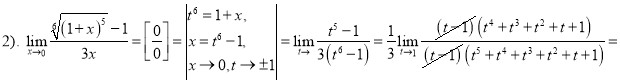
Приклад 1.5 Визначити тип невизначеності та знайти границі:

;     .

Розв’язання

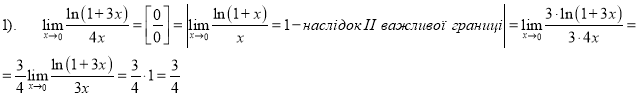
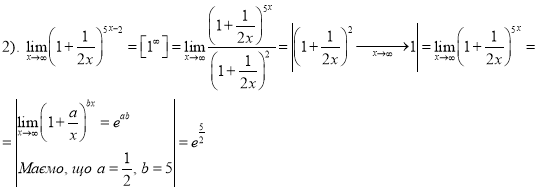
Приклад 2: Дослідити функцію на неперервність. Визначити тип точок розриву та схематично побудувати графік функції.

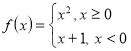
Розв’язання:

. Обстежимо функцію в т. х₀=0.

1. знайдемо значення функції в точці х₀=0: ;
2. знайдемо границі справа і зліва: 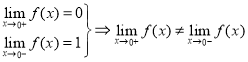- тому т.х₀=0 є точкою розриву І роду. Розрив у вигляді «стрибка»
3. Робимо висновок: функція розривна в т. х₀=0 .

Будуємо схематично графік

Приклад 3. Дослідити функцію на неперервність, наявність асимптот. Визначити тип точок розриву та побудувати схематично графік функції.

Розв'язання:

.

Обстежимо функцію в т. х₀=0:

1.          знайдемо значення функції в точці х₀=0: 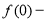невизначена;
2.      знайдемо границі справа і зліва: 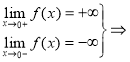- тому т.х₀=0 є точкою розриву ІІ - роду.
3. Робимо висновок: функція не є неперервною в т. х₀=0 .

Обстежимо функцію в т. х₀= -1:

1.   знайдемо значення функції в точці х₀= -1: 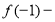невизначена;
2.    знайдемо границі справа і зліва: 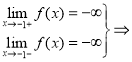- тому т.х₀= -1 є точкою розриву ІІ - роду.
3. Робимо висновок: функція розривна  в т. х₀= -1 .

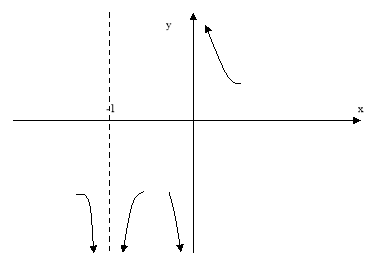Будуємо схематично графік:

 

 

 

 

 

 

 

 

V.  Практична частина. Виконання індивідуальних завдань відповідно власного варіанту.

Рекомендації:

1. Одержати у викладача номер свого варіанту (номер за списком);
2. Виписати числові значення  a, b, c, m, n, k з таблиці варіантів параметрів (доданок 1 з практичного заняття №1), які відповідають вашому варіанту;
3. Записати умови задач з підставленими в них значеннями параметрів;
4. Розв’язати завдання.

Завдання 1: Визначити тип невизначеності та знайти границі.

Примітка: на оцінку «3» студент довільно вибирає з кожної стрічки одну вправу.

на «4»  - довільно  з п. 1.1 та 1.5 вибрати дві вправи.  №1.2 – 1.4 виконати в повному обсязі.

на «5» - необхідно знайти  всі границі з п. 1.1 – 1.5

	А	Б	В
1.1
1.2			-
1.3			-
1.4		-	-
1.5

Завдання 2^[1]: Дослідити функцію 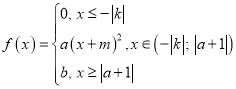  на неперервність. Визначити тип точок розриву та схематично побудувати графік даної функції.

Завдання 3^[2]:  Дослідити функцію на неперервність, наявність асимптот. Визначити тип точок розриву та побудувати схематично графік функції.

VI. Підсумок заняття:

Висновок. Продовжити речення:

На практичному занятті я закріпив …………

Мені було важко при …………………….

Мені сподобалось ………………….

VII. Домашнє завдання:

• повторити теоретичний матеріал,
• закінчити завдання на оцінку «4», «5».

^[1]  На оцінку «3» дослідити функцію лише на неперервність. Обов’язкове завдання на «4»  - виконати в повному обсязі;

 

^[2] Обов’язкове завдання на «5». Причому, завдання №2 виконувати не потрібно.