ГЕОМЕТРИЧНІ ПЕРЕТВОРЕННЯ НА ПЛОЩИНІ

Практичні наробки до теми            

 

Автор

Маєвська Лілія Іванівна, учитель математики   Опорного закладу «Торецька  загальноосвітня школа  I – III ступенів № 6» військово – цивільної  адміністрації  м. Торецька  Бахмутського району     Донецької області

            

 

 

 

В сучасній математиці однією з провідних ідей є ідея перетворень, за допомогою якої доводять твердження з різних розділів математики, які виходять за межі шкільного курсу.      Пропоную матеріал, в якому приділена увага таким перетворенням, як рух, проілюстровано застосування його властивостей для розв’язання деяких цікавих  задач. Розв’язання таких задач сприяє формуванню наукового світогляду, нестандартного мислення, пізнавального інтересу здобувачів освіти.                                                                           

 

«Оскільки природа є початок руху і зміни, а предмет нашого дослідження - природа, то не можна залишати нез'ясованим, що таке рух; адже незнання руху необхідно тягне за     

собою незнання природи»

Аристотель  

ПЕРЕТВОРЕННЯ ФІГУРИ. РУХИ

 

 Означення. Наслідки

 

   Метод геометричних перетворень є досить продуктивним методом розв’язування геометричних задач. Математична теорія симетрії, симетрія у живій та неживій природі, мистецтві, архітектурі, інженерії отримали спільне підґрунтя у геометричних перетвореннях.

   В геометрії розглядають деякі функції, які мають різні значення, вони кожній точці ставлять у відповідність точку. Ці функції називаються геометричними перетвореннями.

Геометричні перетворення мають велике значення в геометрії. За їх допомогою визначають такі важливі геометричні поняття, як рівність та подібність фігур.

 

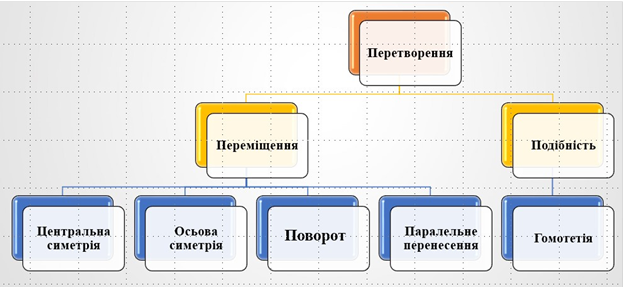
                                                                                                  Рис. 1                                     

Геометричні перетворення дають новий ефективний метод розв’язування задач, який дозволяє у певних випадках полегшити доведення теорем і розв’язування задач.

  Поняття перетворення в геометрії насамперед виникло з розгляду рухів. Найбільш важливою особливістю рухів, з точки зору геометрії, є збереження величини і форми фігури.  Фігура під час руху зберігає свою форму, вона така ж в кінці, як і на початку. Таким чином, якщо брати тільки початковий і кінцевий моменти руху, то ми можемо встановити відповідність між точками фігури в початковому і кінцевому її положенні, при якому кожній точці М фігури F у початковому положенні тіла ставиться у відповідність точка, у яку переходить точка М, коли фігура  тіла F переміститься з початкового положення у кінцеве. При цьому, якщо точки М і N фігури F перейдуть в точки М' і N', то відрізки МN і М'N' рівні між собою. 

 

 

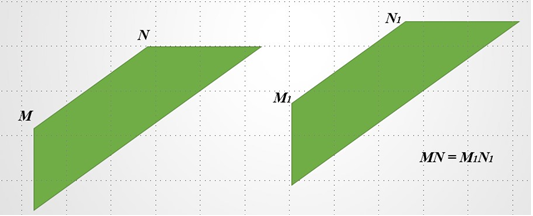
                                                                                    Рис. 2

В цій роботі розглядаються саме такі види перетворень. Далі називаємо їх рухами або переміщеннями. 

Переміщенням (або рухом) називається перетворення фігури, внаслідок якого зберігаються відстані між точками даної фігури.

Властивості переміщення:

-            два послідовні переміщення знову дають переміщення;

-            перетворення, обернене до переміщення також є переміщенням;

-            внаслідок переміщення точки, що лежать на прямій, переходять у точки, що лежать на прямій, і порядок їх взаємного розміщення зберігається;

-            при переміщенні прямі переходять у прямі, промені – в промені, відрізки – у відрізки;

-            внаслідок переміщення зберігаються кути між променями.                     

Дві фігури називаються рівними, якщо вони суміщаються переміщенням

 

Властивості рухів  в таблиці                 

   Властивості геометричних перетворень представимо  у вигляді таблиці. Так як головна мета роботи – моделювання ситуацій і розв’язання їх за допомогою геометричних перетворень (зокрема рухів), то доведення властивостей не є обов’язковим. Головне  вміти показати застосування цих властивостей.      

                                                                                           

 

 

 

 

 

 

 

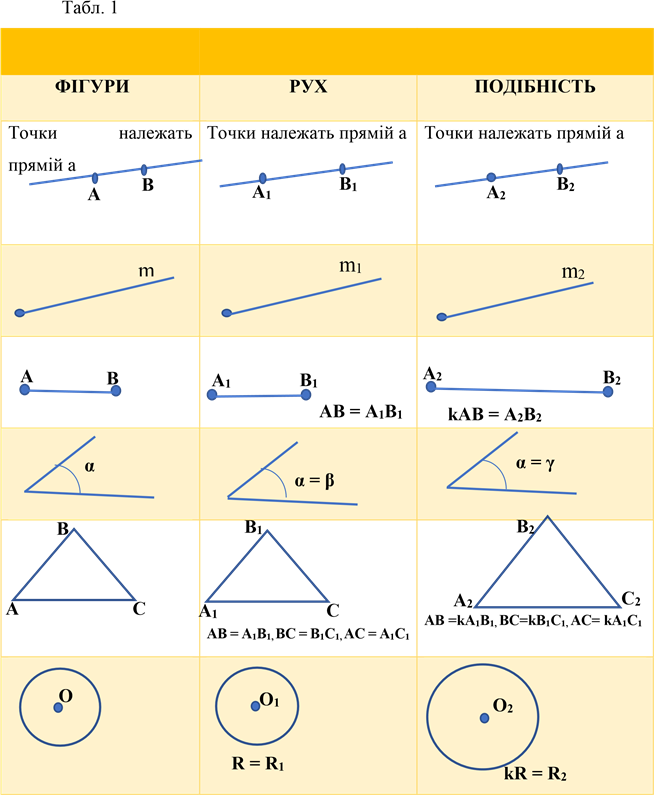
  ПРАКТИЧНЕ ЗАСТОСУВАННЯ ВЛАСТИВОСТЕЙ РУХІВ 

Симетрія відносно точки

Точки А і А₁ називають симетричними відносно точки О, якщо точка О є серединою відрізка АА₁.

Перетворенням симетрії (центральною симетрією) відносно точки О називається таке перетворення фігури F у фігуру F₁, внаслідок якого кожна точка А фігури  F  переходить у точку А₁ фігури  F₁, симетричну  А відносно точки О.

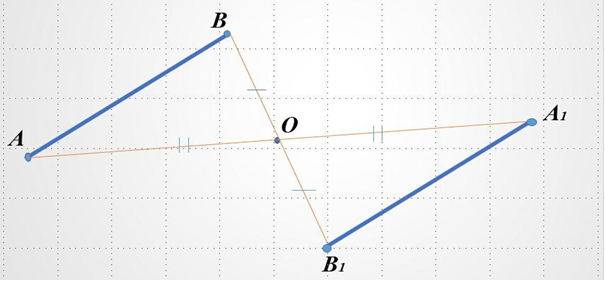
                                                                           Рис. 3

 

Основна властивість осьової симетрії: осьова симетрія є переміщенням.

Центральна симетрія перетворює пряму на паралельну їй пряму або в туж саму пряму; відрізок - на відрізок (Рис. 3); многокутник на рівний йому многокутник.

Фігуру називають симетричною відносно точки О, якщо для кожної точки даної фігури точка, симетрична їй відносно точки О, також належить цій фігурі.

Якщо перетворення симетрії відносно точки О переводить фігуру F у себе, то така фігура називається центрально-симетричною, а точка О – центром симетрії фігури  F.

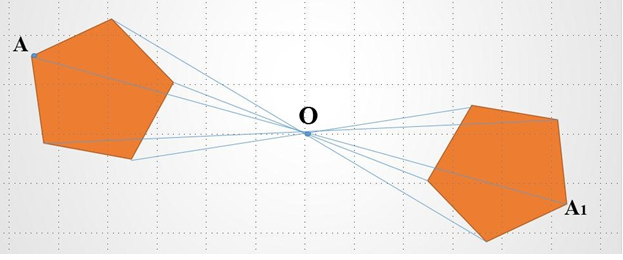
                                                                                                       Рис.4

 

Симетрія – в широкому і вузькому розумінні є тією ідеєю, яку людина протягом століть намагалася осягнути і створити порядок у всіх фізичних явищах. І наш Всесвіт з усіма його складнощами, мабуть, побудують у майбутньому відповідно до понять про симетрії.

З симетрією людина зустрічається  скрізь – в природі, техніці, мистецтві, науці. Поняття симетрії проходить через всю багатовікову історію людської творчості. Принципи симетрії відіграють важливу роль у фізиці, математиці, хімії, біології, музиці та архітектурі.

Задача 1. Дано кут АВС і точку О всередині його. Через точку О провести прямую так, щоб відрізок цієї прямої, який лежить між сторонами кута, ділився точкою О навпіл.

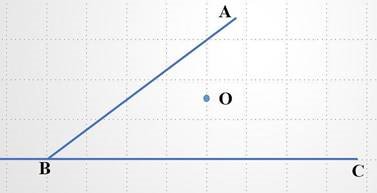 Розв’язання.  

Будуємо В^'С' симетричноВС і відносно точки О. Для цього проводимо перпендикуляр ОК до ВС. На продовженні ОК

відкладаємо відрізок 

                                       Рис. 5                              ОК' = ОК. Проведемо К'С'||ВС.

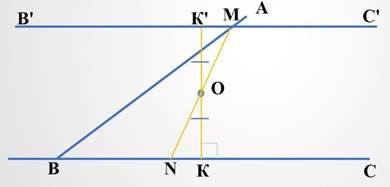Відрізок В^'С' перетинається з ВА в точці М. Проводимо відрізок МО, продовжуємо його до перетину з ВС в точці N. Відрізок      МN    –        шуканий,

оскільки точка М симетрична  

                                                                  точці N відносно т.О, значить МО = ОN. 

Рис. 6

 Задача 2. Дано кут АВС і точку О в середині нього. Через точку О провести пряму так, щоби трикутник, який відтинає його від кута, мав найменшу площу.

            

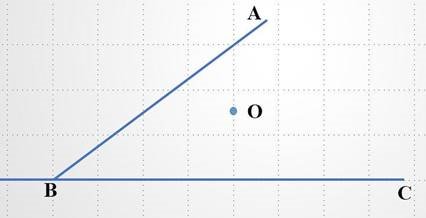
Розв’язання.  

Перша частина побудови аналогічна         побудові     в задачі1.    Отримали відрізок МN, який точкою О ділиться навпіл. 

                                                         Рис. 7     Доведемо, що отриманий       трикутник ВМN має найменшу площу.

 

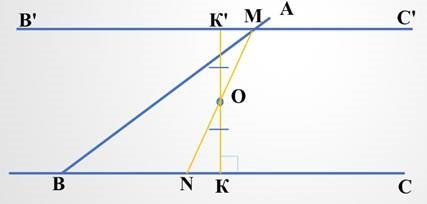Для цого проведемо через точку О довільну пряму РQ, яка перетинає сторони кута АВС в точках Р і Q. Доведемо,          що     площа трикутника BQP, більше площі трикутника ВМN. 

                                          Рис. 8                                             

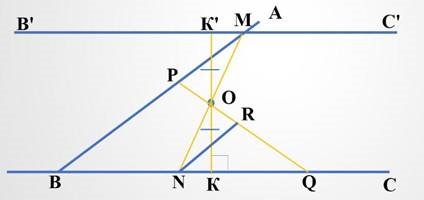Проведемо NR    ||        РМ. ∆PMO = ∆NOR за другою

ознакою      рівності трикутників ( NO = OM, оскільки точки M і N симетричні відносно 

                                      Рис. 9

точки О, кути РОМ і NОR рівні як вертикальні, а РМО = ОNR як внутрішні різносторонні при РМ||NR, MN – січна. 

Звідси S_∆POM = S_∆NOR.

S_∆BMN = SBPON + S_∆POM

S_∆BPQ = SBPON + S_∆NOR + S_∆NRQ, звідки можна впевнитися, що S_∆BMN < S_∆BPQ.

Висновок. ∆ВMN має найменшу площу серед трикутників, які відтіняються від кута АВС прямими, які проходять через точку О.

 

 

 

 

Симетрія відносно прямої

Перетворенням симетрії (осьовою симетрією) відносно прямої а називається таке перетворення фігури  F у фігуру F₁, внаслідок якого кожна точка  фігури F переходить у точку  фігури  F₁ симетричну  відносно прямої а.

 

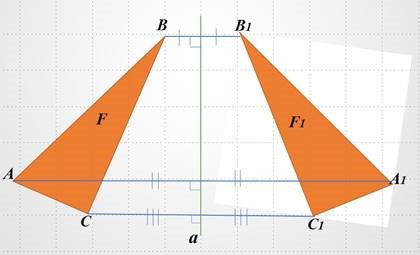
                                                 Рис. 10

Основна властивість осьової симетрії: осьова симетрія є переміщенням. 

Осьова симетрія перетворює: пряму на пряму; відрізок - на відрізок; многокутник на рівний йому многокутник.

Точки, що належать осі симетрії, відображаються самі на себе.

Точки А і А₁ називають симетричними відносно прямої а, якщо пряма а є серединним перпендикуляром відрізка АА₁.

 

Задача 3. Дано гострий кут АВС і точка М всередині нього. Знайти на стороні кута такі точки Х і У, щоби ∆МХУ мав найменший периметр.

Розв’язання. 

Будуємо точку М₁ симетрично точці М відносно променю ВА і точку М₂ симетрично точці М відносно променю ВС. Пряма М₁М₂ перетинає ВА і ВС відповідно в точках Х і У. ∆МХУ – шуканий.

Треба довести, що периметр ∆МХУ буде найменшим. Візьмемо довільні точки

Х₁ і У₁ на сторонах кута АВС , відмінні від точок Х і У, і доведемо, що 

РМХ1У1  РМХУ. 

Р_МХУ = MX + XY + YM = M₁X + XY + YM₂ = M₁M₂, оскільки M₁X = МХ, МУ = YM₂  як симетричні відрізки. 

Р_МХ1У1 = МХ1 + Х1У1 + У1М = М1Х1 + Х1У1+ У1М2, оскільки 

М₁Х₁ = МХ_1, У₁М = У₁М₂ як симетричні відрізки.

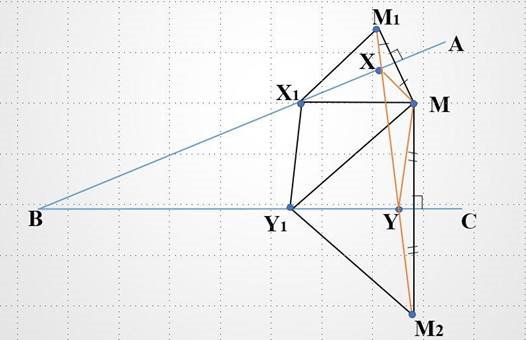
                                                       Рис. 11

Довжина ламаної М₁Х₁У₁М₂ більше за довжину відрізка М₁М₂, звідки

 РМ Х1У1  РМХУ. 

А це значить, що Р_МХУ – найменший.

 

 

 

 Поворот

Поворотом фігури Fнавколо точки О на кут α називається перетворення фігури F  у фігуру F₁ внаслідок якого кожна точка  фігури F переходить  у  точку  фігури F₁ так, що OА₁ = OА і кут АOА₁ = α.

Точку О називають центром повороту, а кут α – кутом повороту.

 

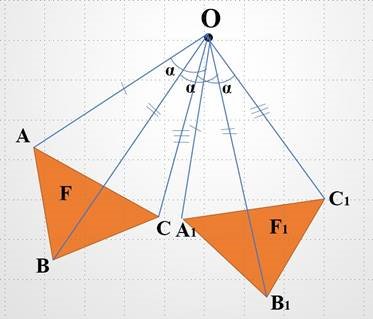
                                      Рис. 12

Основна властивість повороту: поворот с переміщенням. Тобто якщо фігура F1 - образ фігури F при повороті, то F = F1.

Якщо внаслідок повороту навколо деякої точки О фігура F переходить у себе, то кажуть, що ця фігура має поворотну симетрію (або симетрію обертання).

 

 

 

 

 

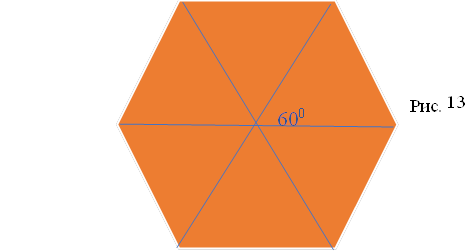
Правильний шестикутник переходить у себе при поворотах на кути кратні 60⁰.

Правильний трикутник переходить у себе при поворотах на кути кратні 120⁰. 

 

 

 

 

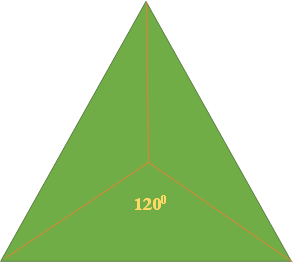
                                                                                              Рис. 14

 

 

Якщо внаслідок повороту навколо деякої точки О фігура F переходить у себе, то кажуть , що ця фігура має поворотну симетрію( або симетрію обертання).

Фігура, що має дві осі симетрії, переходить у себе при поворотах на кути кратні 90⁰.  

Фігура переходить сама в себе при поворотах на кути кратні 45⁰.

 

                                                                      Рис. 15

 

 

Задача 4. 

Побудувати рівносторонній трикутник, вершини якого лежать на паралельних прямих.

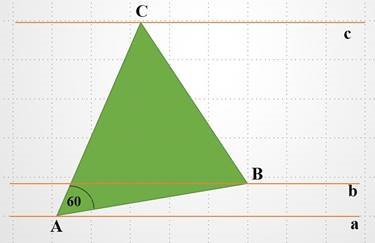
                                                                Рис. 16

 

 

Аналіз

Нехай ∆ АВС – заданий. Вершини А, В, С лежать відповідно на прямих а,b, c. Під час повороту з центром в точці В на 60⁰ за годинниковою стрілкою точка С переходить в точку А. А це значить, що треба зробити поворот прямої а з центром в точці В за годинниковою стрілкою на 60⁰. При цьому пряма а переходить в пряму а₁, яка перетинає пряму с в точці А.

Під час повороту  точка А переходить в точку С.

Бачимо, що необхідно провести поворот (АВ) = АС. Отримуємо шуканий трикутник АВС.

Побудова

1)                На прямій b ставимо точку В.

2)                Відтворюємо поворот (а) = а₁. Прямі а і а₁ перетинаються в точці А. 

3)                Відтворюємо поворот (А) = С.

4)                ∆АВС – шуканий.

 

Доведення

5)                За побудовою: точки А, В, С лежать на паралельних прямих а, b, c і кут АВС дорівнює 60⁰. Окрім того АВ = ВС в силу пороту (А) = С, відповідно ∆АВС –дійсно  шуканий.

Зауваження. Задача має два розв’язання, відмінні одне від одного в залежності з якої сторони знаходяться точки А і С відносно точки В. Задача має розв’язок при будь яких відстанях між прямими  а, b, c відмінних від нуля.

 

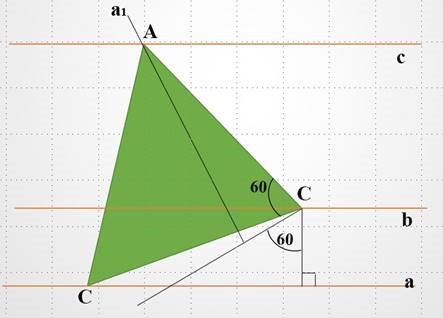
                                                          Рис. 17 

Паралельне перенесення

Паралельним перенесенням фігури F у напрямі променю ОА    на відстань а називається таке перетворення фігури F у фігуру F₁, внаслідок якого кожна точка М фігури F переходить у точку М₁ фігури F₁ так, що промені  ММ₁ і ОА співнапрямлені і ММ₁ = а.

У прямокутній системі координат паралельне перенесення , яке переводить точку ( x; y) в точку ( x_1; y₁), задається формулами x₁ = x + а; y₁= y + b, де a і b – деякі числа, одні й ті самі для всіх точок площини.

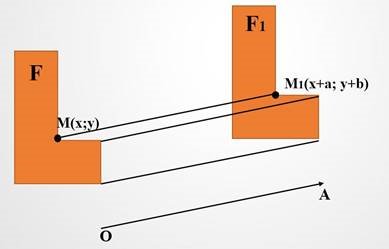  Рис. 18

Основна властивість         паралельного     перенесення:                 паралельне перенесення є переміщенням.

При паралельному перенесенні пряма переходить у паралельну пряму (або в себе); промінь переходить у співнапрямлений  промінь.

При паралельному перенесенні точки переміщуються вздовж паралельних прямих ( або однієї прямої) на ту саму відстань.

 

Задача 5. 

Побудувати трапецію за діагоналями і основами.

Аналіз.

 

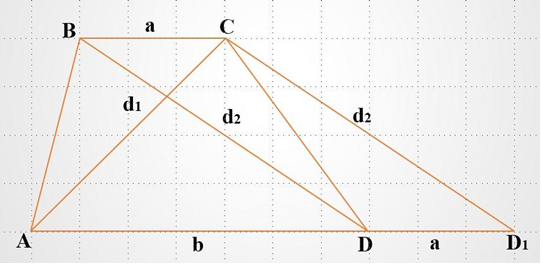
                                                                                                                        Рис. 19

Нехай трапеція АВСD (АD = b, BC = a, AC = d, BD = d₂) – задана. 

Виконаємо паралельний перенос відрізка ВО вздовж прямої АD на відстань а.

Тоді відрізок ВО перейде у відрізок СD_1.

DBCD₁ – паралелограм ( ВС||DD₁, BD||CD₁ за побудовою).

Значить ВС = DD₁ = а, BD = CD₁ = d_2.

AD₁ = AD + DD₁ = b + а.

B ∆ACD₁   AC = d₁, CD₁ = d₂, AD₁ = b + a.

Робимо висновок, що побудова зводиться до побудови ∆ACD₁ за трьома сторонами.

Побудова.

 

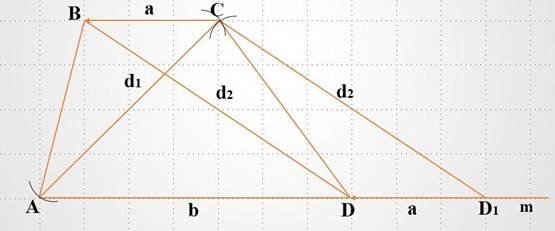
                                                                        Рис. 20

1)                На довільній прямій m відкладаємо відрізок AD₁ = b + a.

2)                Проводимо кола О₁(А;d₁) і O₂(D₁;d₂), С – точка їх перетину. 

3)                Виконуємо паралельний перенос відрізка CD₁ вздовж прямої m на відстань а у напрямку точки А. СО₁ переходить в BD.

4)                Трапеція АВСD – шукана.

Доведення.

За побудовою АС = d₁ і BD = CD₁ = d_2.

Окрім того, так як перенос здійснюється по прямій m, то точки А, D, D₁ лежать на одній прямій. Значить AD₁ = AD + DD₁ і AD = AD₁ -  DD₁.

Оскільки перенос відбувається на відстань а, то DD₁ = ВС = а, і  AD = b + a – а = b.

Робимо висновок. АВСD – шукана трапеція.

 

 

 

 РОЗВ’ЯЗУВАННЯ ЗАДАЧ ПРАКТИЧНОГО ЗМІСТУ 

Задачі на рух на місцевості

Задача 1. По одну сторону від дороги розташовані два селища А і В. Де біля дороги необхідно побудувати автобусну зупинку, щоби сума відстаней від неї до цих селищ була найменшою.  

Розв’язання.

Нехай точки А і В – задані селища, пряма m – дорога.  Будуємо точку В₁ симетрично точці В відносно прямої m. Пряма АВ₁ перетинає пряму m в точці С. Доведемо, що точка С – шукана.

Для цього візьмемо довільну точку С₁ на прямій m, відмінну від точки С.

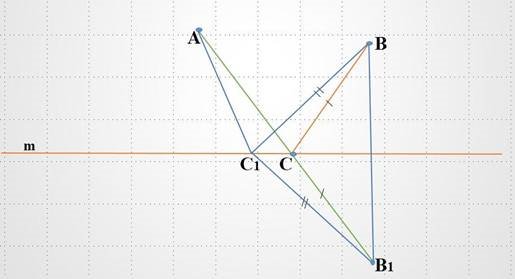
                                                                                    Рис. 21

Оскільки Точки В і В₁ симетричні відносно прямої m, то С₁В = С₁В₁.

Тому АС₁ + С₁В = АС₁ + С₁В₁.

 

 

 

Задача 2. Маршрут туристів  пролягає з пункту А до пункту В. Який шлях їм треба пройти вздовж дивовижного водоспаду (СD), щоби весь маршрут АСDВ був найкоротшим?

                                                                                         Рис. 22

Розв’язання.

Переформулюємо умову задачі. Нехай маємо пряму а  і точки А і В по одну сторону від неї. У якому місці прямої а потрібно провести ділянку туристичного маршруту  СD = d, щоб довжина ламаної АСDВ була найменшою?

 

 

 

 

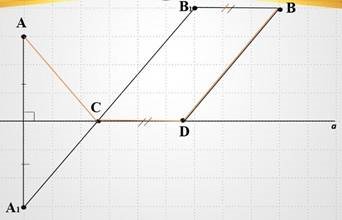
                                                                                                    Рис. 23

Перенесемо точку В паралельно прямій а на відрізок ВВ₁ = d. Довжина ламаної АСВ₁ на d менше від довжини ламаної АСDВ. Тепер задача зводиться до відшукання точки С на прямій а. Для цього знайдемо точку А₁ симетричну точці А відносно прямої а. З’єднаємо точки А₁ і В₁. Точка перетину А₁В₁ з прямою а і буде шуканою точкою С на прямій а. Від точки С відкладемо відрізок СD = d. Залишилося з’єднати точки D і В. АСDВ – шуканий найкоротший туристичний маршрут.

Задача 3. Два міста А і В розташовані по різні сторони прямолінійної річки з паралельними берегами. Необхідно побудувати міст MN, перпендикулярний до берегів, щоби відстань AMNB була найкоротшою.

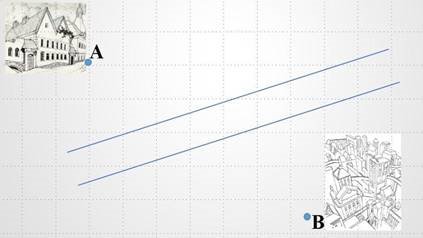
                                                                                                    Рис. 24

Розв’язання

Якщо би не ріка, то найкоротший шлях був би відрізок АВ. 

Міст (M₁N₁) через річку повинен проходити перпендикулярно до берегів. Треба визначити його місто розташування відповідно до вимог.  Спробуємо знехтувати річкою і «приблизити» місто В до берега в перпендикулярному напрямку ( M₁N₁ || ВВ₁). Тоді відстань AMNB = AMB₁B. 

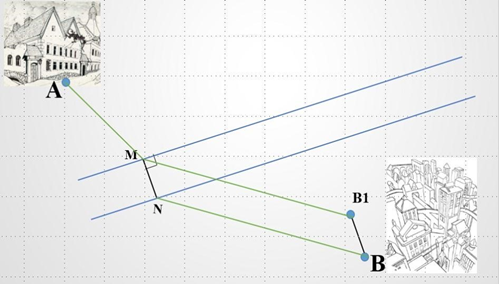                                                                                                             Рис. 25 Залишається вибрати точку М на березі таку, щоб ламана АМNВ була найменшою. Для цього проведемо відрізок АВ₁. Точка перетину цього відрізка з лінією берегу і буде шуканою точкою М.

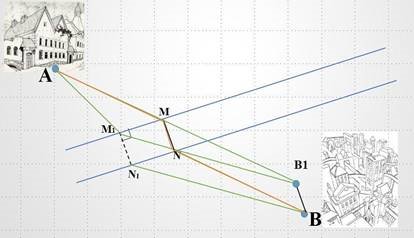
                                                                                                    Рис. 26

Задача 4.  Треба провести водогін між двома містами, які розділені між собою двома  каналами.  

Розв’язання.

Водогін  (M₁N₁) через річку повинен проходити перпендикулярно до берегів. Треба визначити його місто розташування відповідно до вимог.  Знехтуємо річкою і «приблизимо» місто В до берега в перпендикулярному напрямку (M₁N₁ || ВВ₁). Тоді відстань AM₁N₁B = AM₁B₁B. 

Проведемо відрізок АВ₁, тоді знайдемо місце для точки М. А значить MN – шукана ділянка водогону через один з каналів. АМNВ – поки буде найменшої довжини. 

 

 

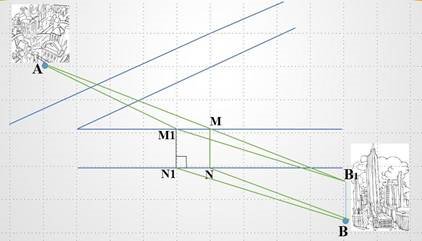
      Рис. 27

                                                     

                                                     

Знайдемо, в якому місці провести водогін через другий канал. Для цього аналогічно першій побудові «приблизимо» місто В до берега в перпендикулярному напрямку (K₁P₁ || ВВ₂). Тоді відстань AK₁P₁B = AK₁B₂B. Проведемо відрізок АВ₂, тоді знайдемо місце для точки K. Будуємо КР||  K₁P₁, отримуємо ділянку водогону КР через другий канал. 

Остаточно маємо ламану АКРМNВ, яка відповідає шуканому водогону між двома містами найменшої довжини.

 

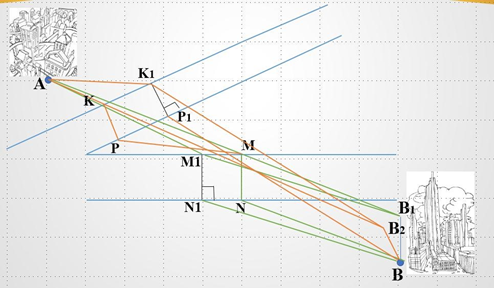                                                                                                      Рис. 28

 

ВИСНОВКИ

Геометричні перетворення додають  математиці естетику, витонченість. Ідея симетрії - орнаменти, сніжинки, архітектурні споруди являються втіленням цієї ідеї.  

Розв’язання усіх  задач супроводжуються малюнками, наочним аналізом ситуації, яка задається умовою задачі. Цей аналіз допомагає визначити відповідний метод розв’язання.

Добірка задач має на меті спонукати учнів  до розвитку навичок та умінь застосовувати отримані знання у практичній, наближеній до життєвої ситуації, будувати та досліджувати математичні моделі задач.

 

СПИСОК ДЖЕРЕЛ

1.        Абламейко, С.В. Обработка изображений: технология, методы, применение. [Текст] / С.В. Абламейко, Д.М. Лагуновский. – Минск: Амалфея, 2000. – 360с.

2.        Баран О.І. Математичні мініатюри. – К.: Ленвіт, 2007

3.        Бевз Г.П. Геометрія чотирикутника. – Х.: ВГ «Основа», 2003

4.        Боровик В.Н. Геометричні перетворення площини. – Суми: Університет. Книга, 2003

5.        Бурда М.І., Савченко Л. М. Геометрія //9 клас//Експериментальний навчальний посібник для шкіл (класів) з поглибленим теоретичним практичним вивченням математики.-К.: Освіта.- 1994

6.        Вишенський В.А. Збірник задач з математики: Навч. Посібник.- 2-ге вид.,К.:-

Либідь, 1993

7.        Кравчук М.О. Геометричні перетворення. Частина 1. – Луцьк. 2018

8.        Кушнір І.А. Методи розв’язання задач з геометрії. – К.: Абрис, 1994

9.        Мурач М.М. Геометричні перетворення і симетрія. -К.:1987

10.   Приймаков О.Г., Молявко О.І. Розв’язування геометричних задач на побудову /Навчальний посібник для викладачів математики, креслення та абітурієнтів. – Х.: Скорпіон, 2003

11.   Приймаков О.Г., Молявко О.І. Цікаві розділи математики 98-11 класи). – Х.: Скорпіон, 2001

12.   Раков С.А., Горох В.П. Компьютерные эксперименты в геометрии // Учебн.

Пособие для учащихся по курсу геометрии.-Х.: РЦНИТ, 1996

13.   Філіпповський Г. Шкільна геометрія в мініатюрах. – К: Грот, 2002

14.   Яцюк О.Г. Основы графического дизайна на базе компьютерных технологий.

[Текст] / Яцюк О.Г. – СПб: bhv, 2002. – 240 с

15.   https://ru.calameo.com/read/00359657853f9ecd4a716/

16.   http://sva.in.ua/geometria9008.php