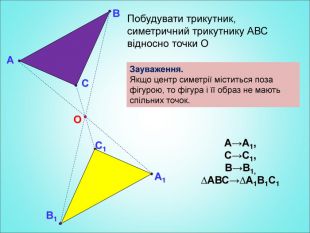
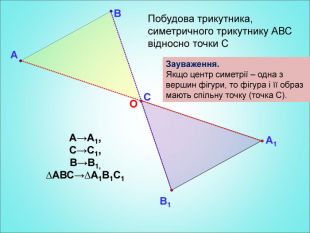
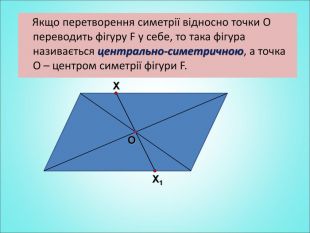
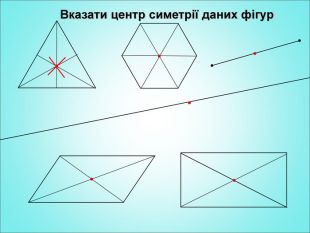
Урок з теми "Симетрія відносно точки"
Про матеріал
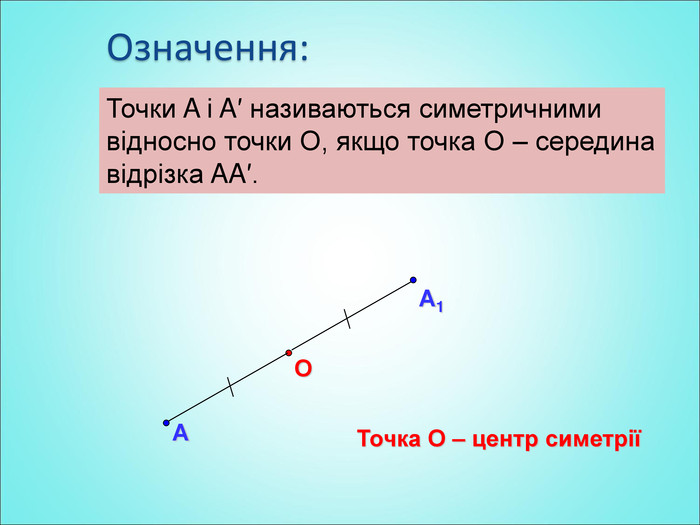
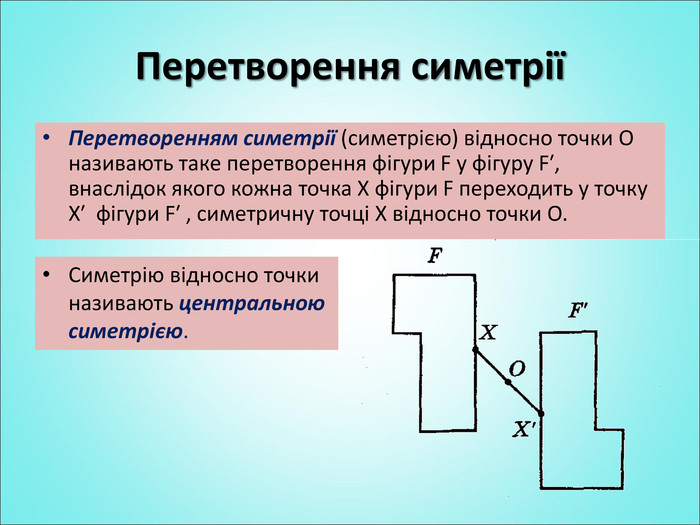
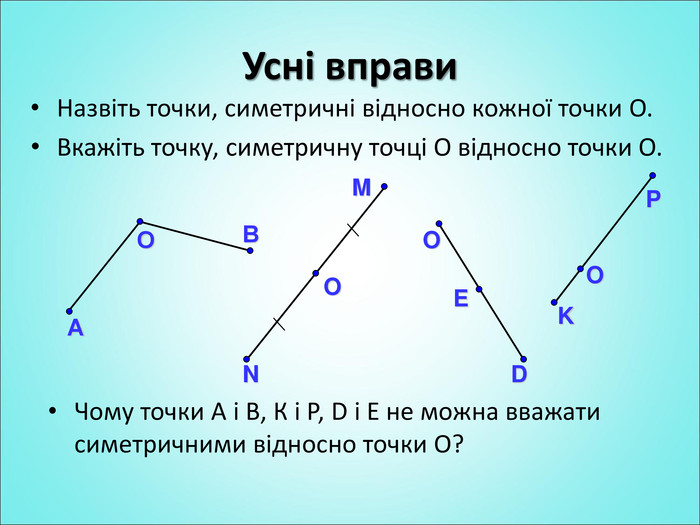
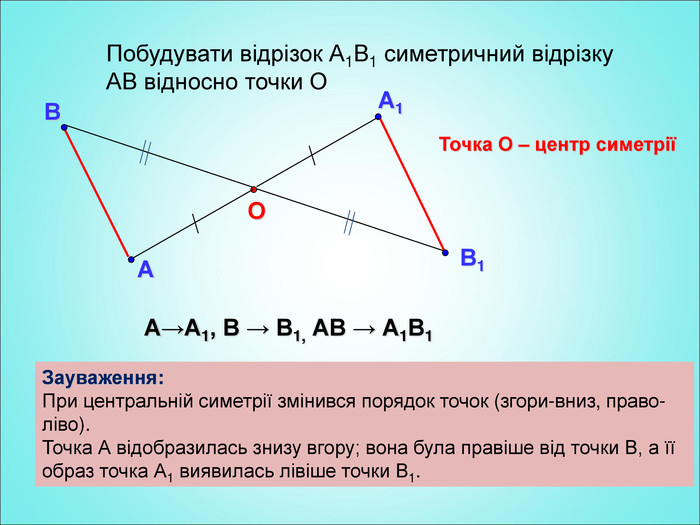
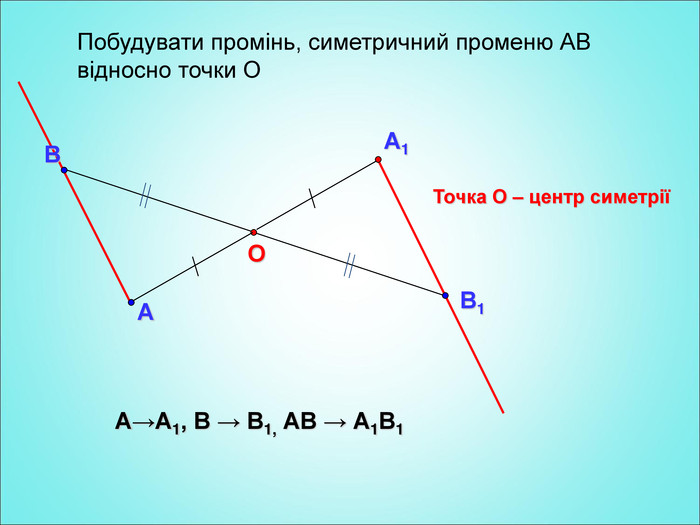
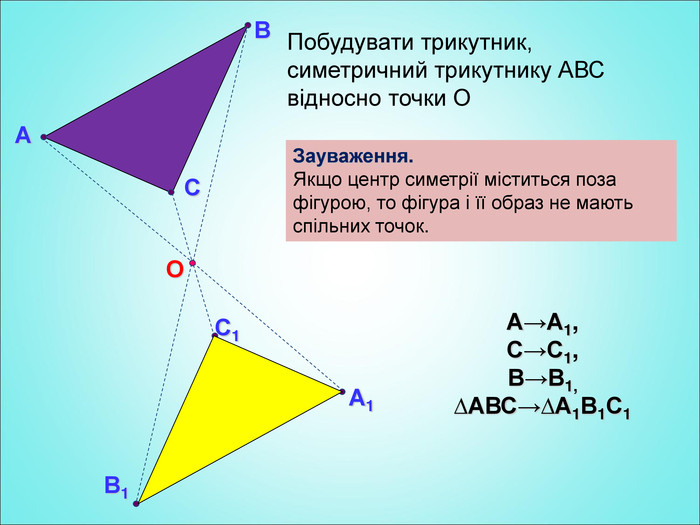
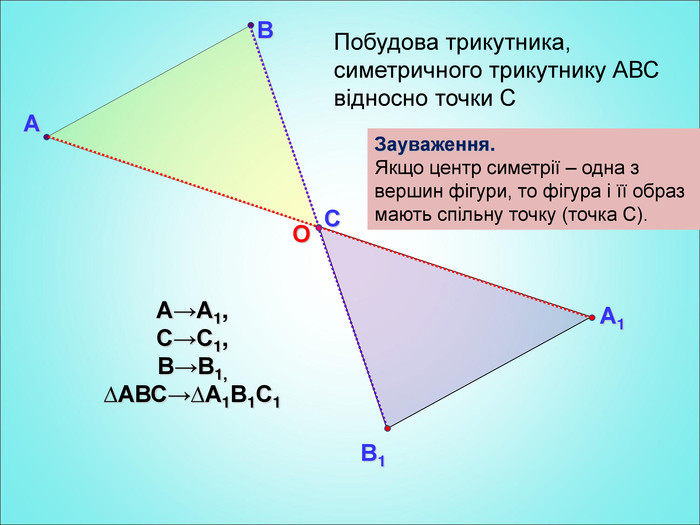
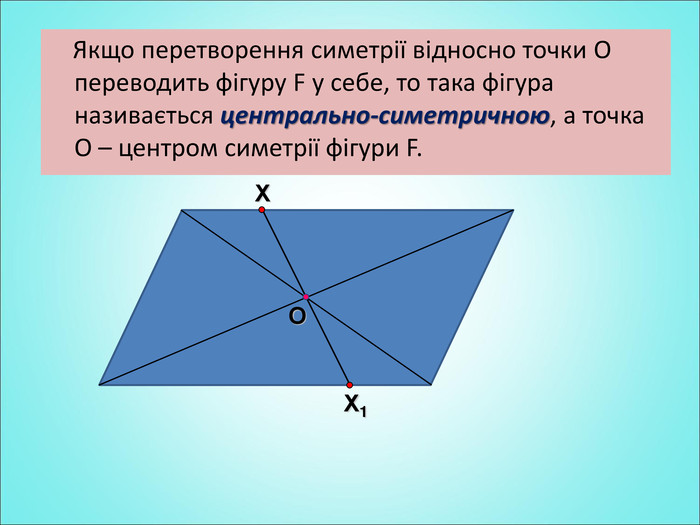
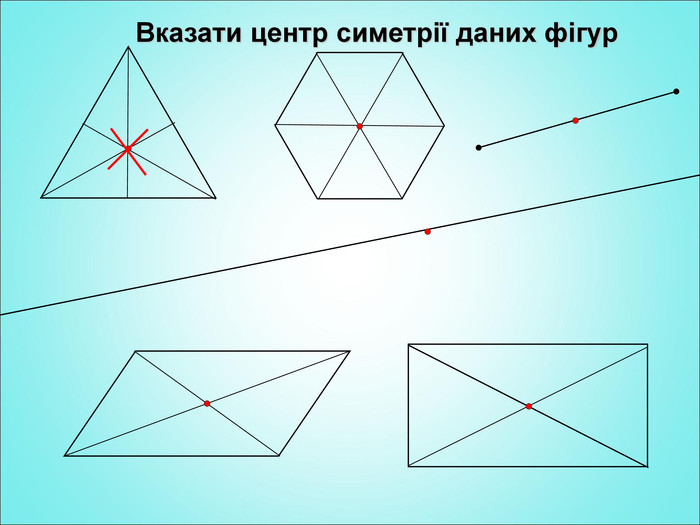
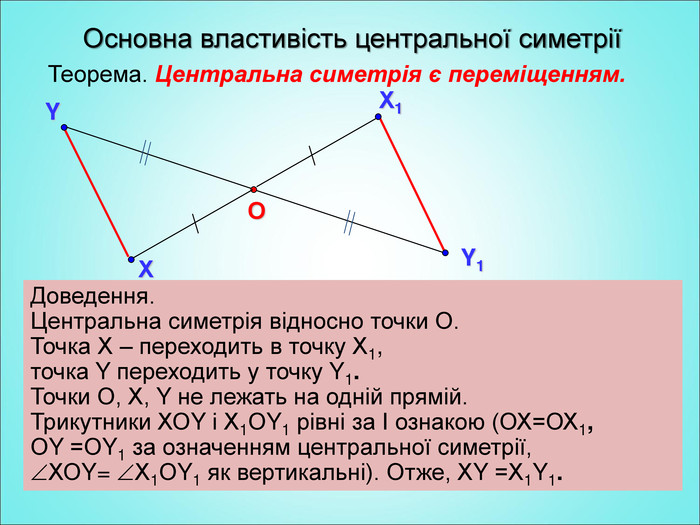
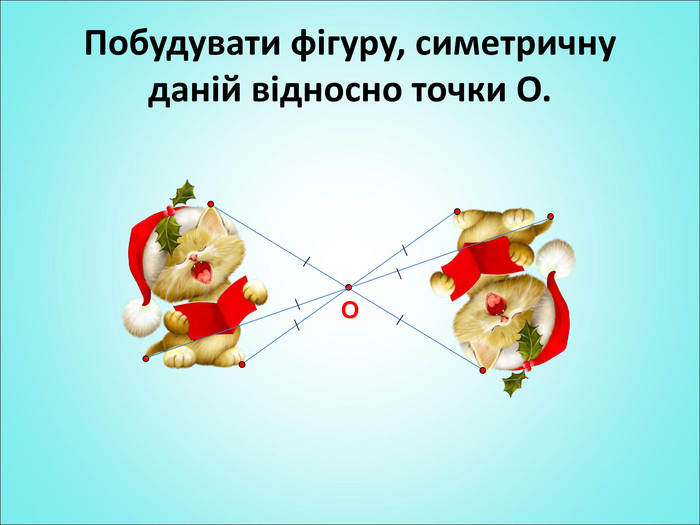
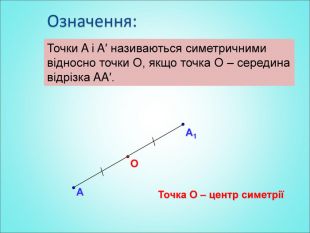
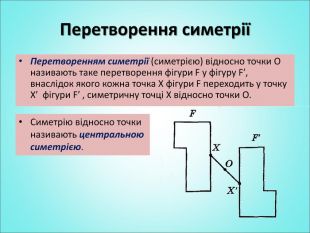
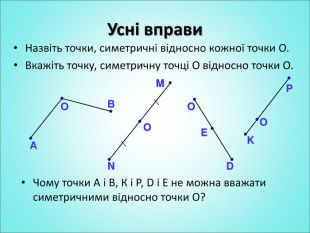
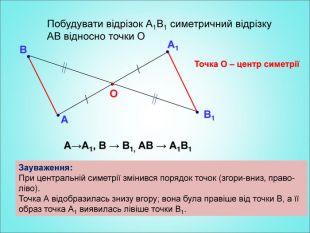
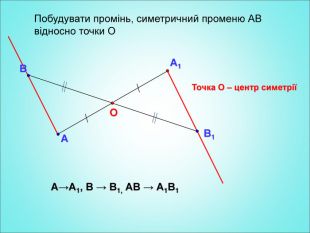
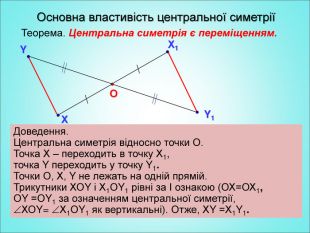
Мета: формування поняття симетрії відносно точки; вивчення властивостей симетрії відносно точки; формування вмінь застосовувати вивчені означення і властивості до розв'язування задач. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
-
Дякую


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку