Практичнна робота: Програмування циклічних процесів з використанням оператора повторення WHILE…DO….

Про матеріал

Навчитися описувати оператор повторення з передумовою на мові програмукваннята розглянути типові задачі. Містить опис оператора повторення While … do…, схему виконання оператора While, приклади розв'язування типових задач

Перегляд файлу

Лабораторна робота

Тема: Програмування циклічних процесів з використанням оператора повторення WHILE…DO….

Мета: Навчитися застосовувати оператор повторення WHILE…DO… для розв'язування задач циклічного характеру.

Засвоїти поняття:

цикл програми;

оператор повторення;

оператор повторення While;

нескінченний цикл;

генератор випадкових чисел.

Вміти:

описувати циклічні процеси за допомогою оператора повторення While;

будувати таблицю покрокового виконання циклу;

використовувати властивості оператора повторення While ;

одержувати випадкові числа потрібного діапазону.

Основні задачі

Перевести задане ціле число з десяткової системи числення в двійкову.

Знайти найбільший спільний дільник двох цілих чисел.

Скоротити дріб.

З'ясувати, чи є задане натуральне число паліндромом.(Наприклад, 121, 342243).

Розкласти число N на прості множники. Результат вивести у вигляді N=p₁(k₁)* p₂(k₂)*…, де p_і – простий множник, k_і – показник степеня.

Визначити номер N числа Фібоначі, при якому сума N перших чисел Фібоначі перевищує задане число M. (Числа Фібоначі визначаються за рекурентною формулою : f₁=1, f₂=1, f_i=f_i-1+f_i-2).

Дано дійсне число А. Знайти серед чисел 1,1+,1++,…, перше, більше за А.

Дано дійсне число А. Знайти таке найменше N, що 1++…+>А.

Дано ціле число М>1. Одержати найбільше ціле К, при якому 4^К<М.

Дано натуральне число N. Одержати найменше число виду 2^K, більше за N.

Індивідуальні завдання

( Вибрати завдання за номером в журналі викладача )

Одержати Р послідовностей К чисел, випадковим чином вибраних з відрізка [a,b], і які задовольняють вказаним умовам.

№	P	K	a	b	Додаткові умови на числа послідовностей
1	5	11	50	1000	перші 5 чисел – парні, останні не парні
2	4	12	20	1200	останні 5 чисел – непарні, інші парні
3	8	13	1	1000	числа з непарними номерами кратні трьом
4	5	14	50	600	числа з непарними номерами кратні чотирьом
5	7	18	30	230	перша половина чисел – парні, друга – непарні,
6	4	16	1000	2000	різниця двох послідовних чисел за модулем не менша за 5
7	9	17	10	1001	кожне друге число кратне семи
8	5	18	200	1200	кожне третє число кратне п’яти
9	7	22	3	300	числа першої половини кратні трьом
10	8	20	4	240	числа другої половини кратні семи
11	3	21	10	1000	сума цифр числа кратна трьом
12	5	22	100	2000	сума цифр числа кратна п’яти
13	5	23	200	5000	різниця двох послідовних чисел за модулем не більша за 5
14	7	24	400	1000	різниця двох послідовних чисел за модулем не більша за 10
15	6	25	1	500	утворюють впорядковану за зростанням послідовність

Обчислити нескінчену суму 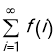із заданою точністю . (Вважати, що потрібну точність досягнуто, якщо обчислено суму декількох перших доданків і наступний доданок виявився за модулем менший ніж , – в цьому разі цей доданок і всі наступні можна уже не враховувати).

№	f(i)	ε	№	f(i)	ε	№	f(i)	ε
		0.01			0.001			0.001
		0.01			0.05			0.006
		0.001			0.005			0.004
		0.0005			0.0001			0.002
		0.002			0.001			0.005

Протабулювати функцію f(x) на відрізку [a,b] з кроком h.

№	f(x)	a	b	h
1		30⁰	60⁰	2⁰
2	sin³x	0		0.1
3	ln	8.4	6.2	-0.2
4	e^x –	0.45	0.61	0.1
5	x²+ln(x² – 4)	3.75	5.5	0.25
6	+sin²x	0.53	0.71	0.1
7	lg\|x² – 2x + 3\|	3.4	5.6	0.2
8		2.1	12.1	1
9		10.5	17.5	1
10	x³–2x+1	0	5	0.3
11	(x+2)³	-3	5	0.5
12		3	9	0.2
13
14	1+	0	100	5
15