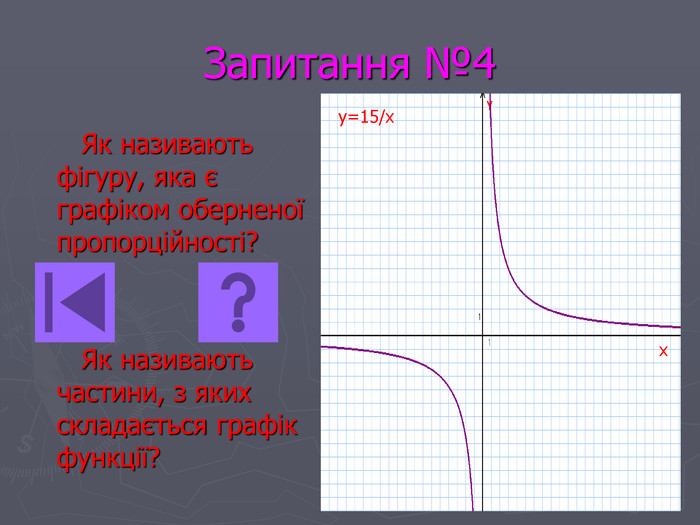
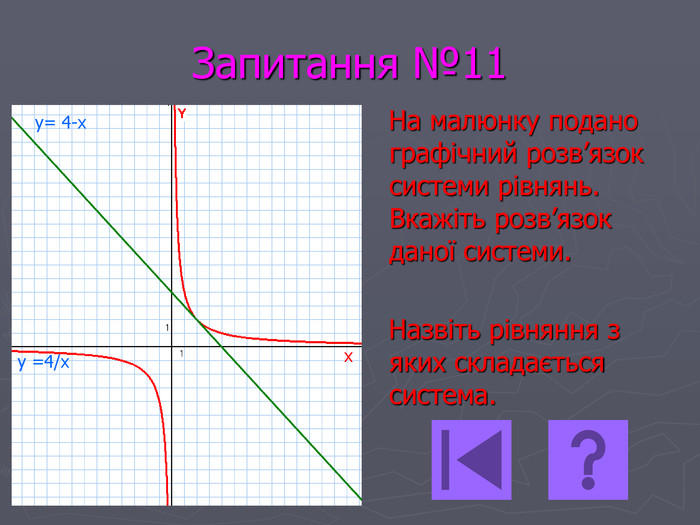
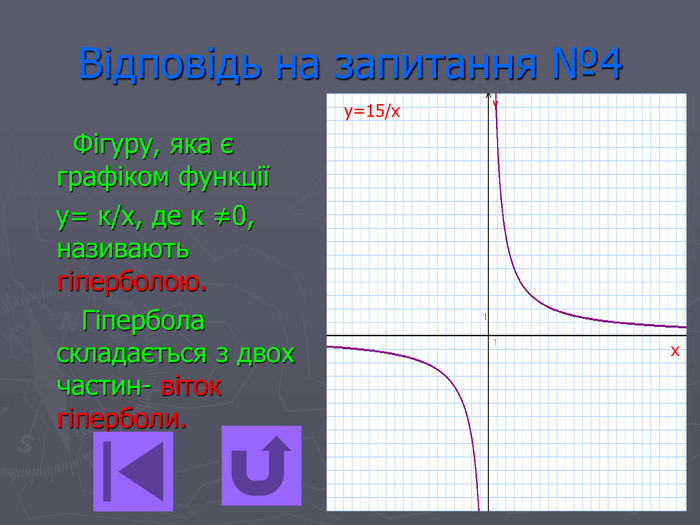
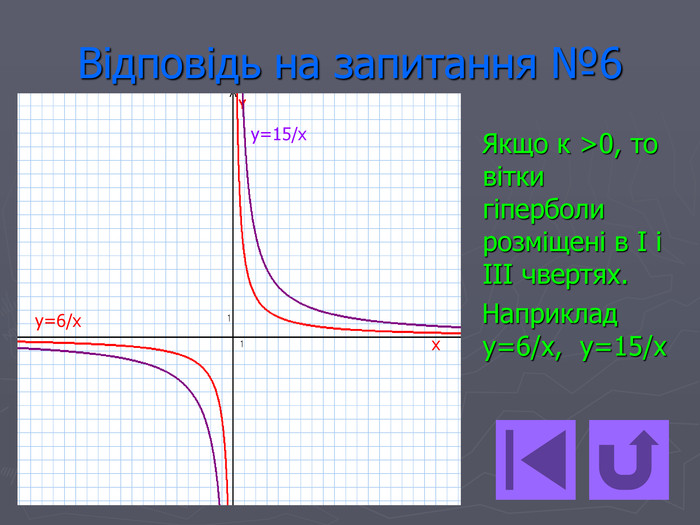
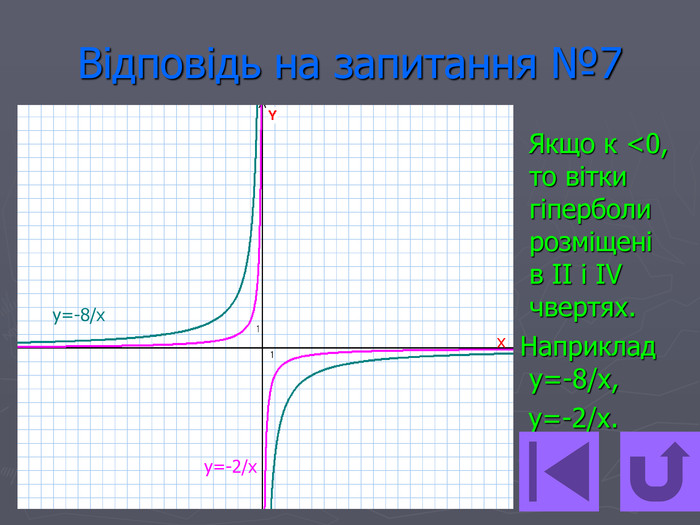
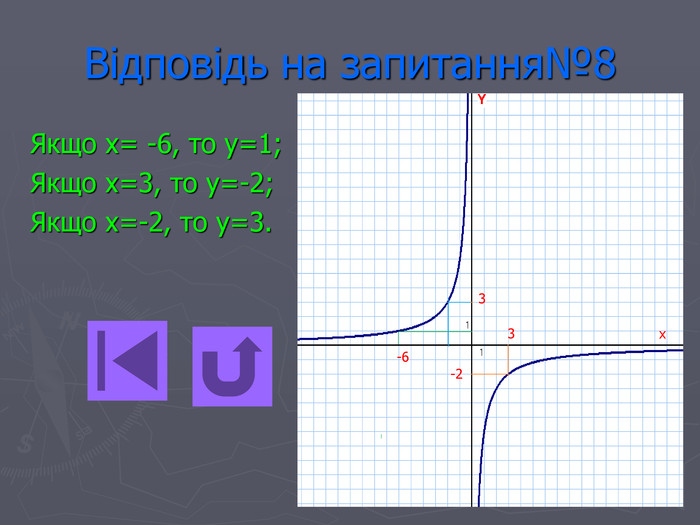
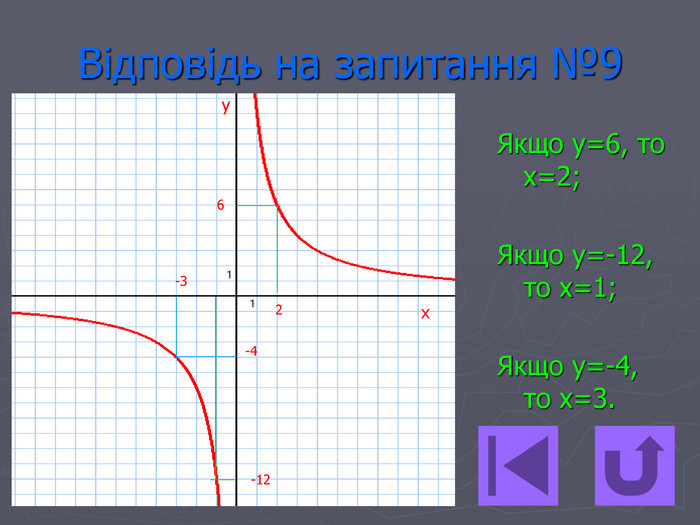
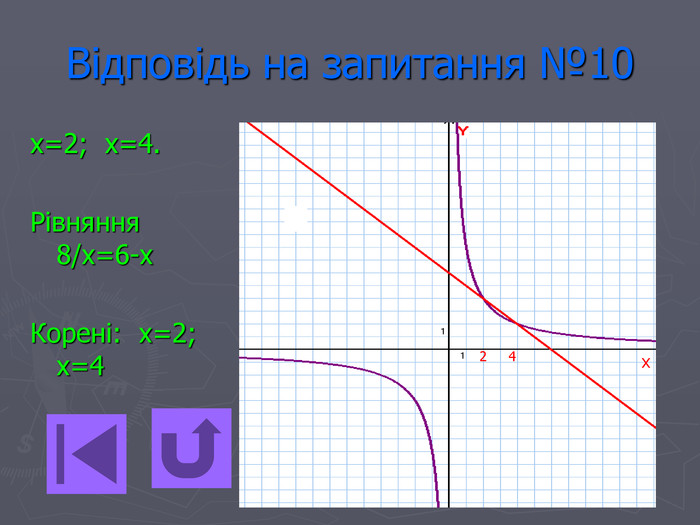
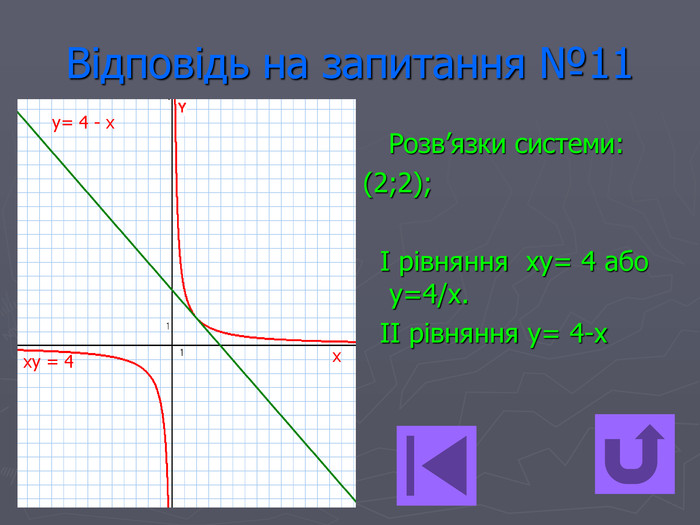
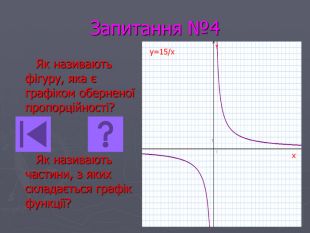
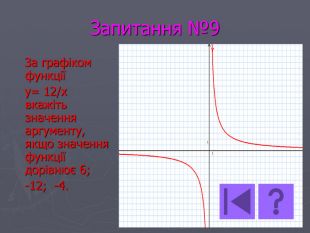
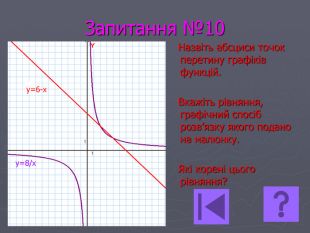
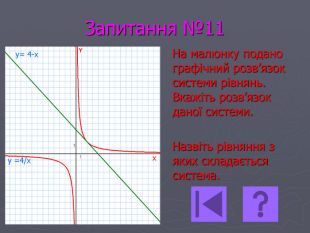
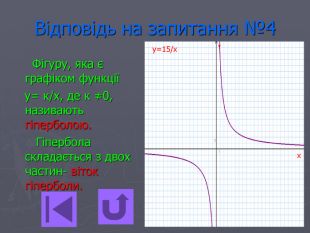
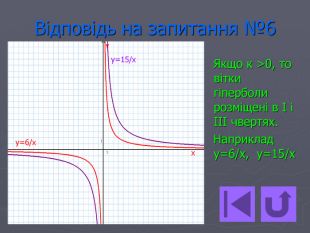
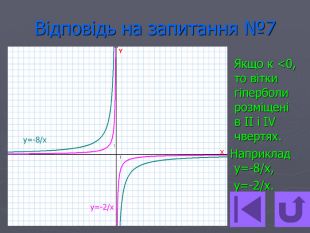
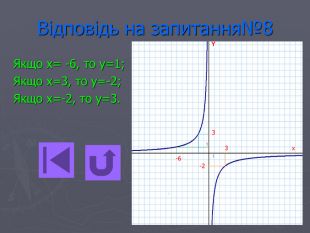
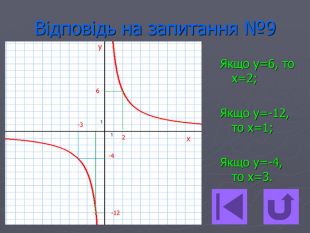
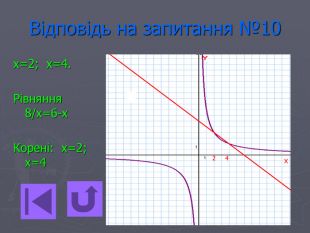
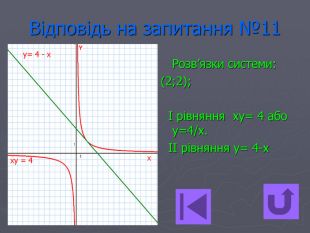
Презентація- вікторина " Функція оберненої пропорційності".
Про матеріал
Дану вікторину можна використати для відпрацьовування знань з теми, а також з метою контролю знань.
Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку