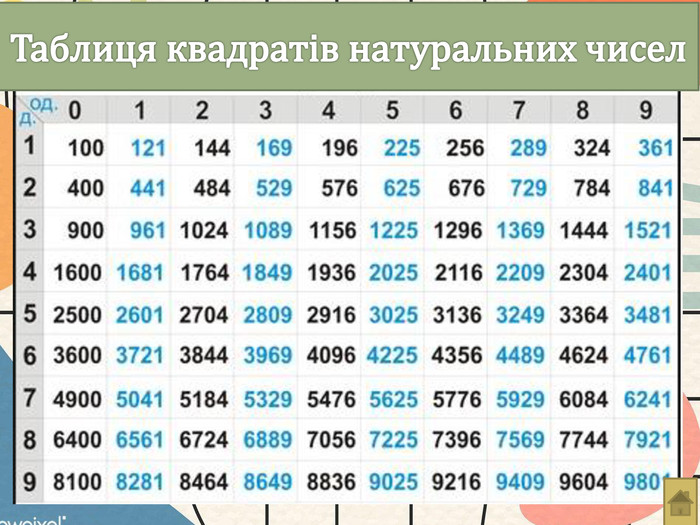
Презентація: "Арифметичний квадратний корінь"

Арифметичний квадратний корінь. Руденко А. С.

Мета уроку:сформувати поняття квадратного кореня, арифметичного квадратного кореня, виробити вміння знаходити арифметичний квадратний корінь із числа, знаходити значення змінної, за яких має зміст вираз, що містить арифметичний квадратний корінь, розв’язувати найпростіші ірраціональні рівняння;

Зміст. Актуалізація опорних знань. Квадратний корінь. Арифметичний квадратний корінь. Таблиця квадратів натуральних чисел. Тотожність (√a)2=a, a≥0 . Добування квадратного кореня. Рівняння √x=a. Раціональні числа Ірраціональні числа. Підбиття підсумків уроку

Актуалізація опорних знань1. Квадрати яких чисел дорівнюють:а) 25; б) 0,04; в) 1 ; г) 0; д) -0,01?2. Чи існують числа, квадрати яких дорівнюють 64; 121; –5; –6; 0; –100?

1. Квадратний корінь. Арифметичний квадратний корінь. Квадратним коренем із числа a називається число, квадрат якого дорівнює a. Арифметичним квадратним коренем із числа a називається невід’ємне число, квадрат якого дорівнює a.𝒂=𝒃 при 𝒂≥𝟎𝒃≥𝟎𝒃𝟐=𝒂 Арифметичний квадратний корінь із числа a позначається √a (a – підкореневий вираз) 

Вираз √𝑎 не має змісту, якщо a < 0 (число 𝑎 - від’ємне). Приклади!

Таблиця квадратів натуральних чисел

Виконання усних вправ. Приклад

2. Тотожність (𝑎)2=a, a≥0 . При a≥0 (𝑎)2=a. Приклад: (9)2=9(7)2=7 

3. Добування квадратного кореня.

4. Рівняння 𝑥=a. 

Розв’язування вправ

це всі дійсні числа, що не є раціональними — тобто не можуть бути записані як відношення цілих чисел, а лише нескінченними неперіодичними десятковими дробами.це числа, які можна подати у вигляді відношення , де m – ціле число, а n – натуральне. Q = { , m є Z, n є N} Кожне раціональне число можна записати у вигляді:- скінченого дробу;- нескінченого періодичного дробу. Раціональні числаІрраціональні числа

Підбиття підсумків уроку1. Що називають квадратним коренем із числа a?2. Що називають арифметичним квадратним коренем із числа a?3. Як позначають арифметичний квадратний корінь?4. Яких значень може набувати підкореневий вираз?5. Чому дорівнює значення виразу (𝑎)2 для будь-якого невід’ємного числа 𝑎? 

Дякую за увагу!

Використана література