презентація Блок "Теоретична механіка, модуль Статика

Технічна механіка. Блок 1 Теоретична механіка. Модуль 1 Статика

ЗМІСТЛекція 1. Вступ. Основні поняття. Аксіоми статики. В'язі та реакції в'язей. Лекція 2. Система збіжних сил. Теорема про три сили. Аналітичне визначення рівнодіючих збіжних сил. Рівняння рівноваги. Лекція 3. Довільна плоска система сил. Момент сили відносно точки. Пара сил. Теореми про пари. Метод Пуансо. Головний вектор та головний момент. Рівняння рівноваги. Три форми рівнянь рівноваги. Теорема Варіньйона. Лекція 4. Плоскі ферми. Методи розрахунку. Метод вирізання вузлів. Метод Ріттера. Поняття про лінії впливу опорних реакцій та зусиль. Рівновага зчленованих тіл. Умова рівноваги важеля. Умова стійкості тіла на перекидання. Кінематичний метод визначення реакцій (принцип можливих переміщень). Лекція 5. Тертя ковзання. Основні закони. Способи визначення коефіцієнта тертя. Кут тертя. Конус тертя. Урахування сил тертя під час розв'язання задач на рівновагу. Опір під час кочення. Лекція 6. Довільна просторова система сил. Момент сили відносно центру та осі. Зв'язок моменту сили відносно точки та моменту сили відносно осі. Теореми про пари. Додавання довільно розташованих сил у просторі. Головний вектор та головний момент. Лекція 7. Аналітичне визначення головного вектора та головного моменту. Рівняння рівноваги довільної просторової системи сил. Можливі випадки приведення системи. Залежність головного моменту від вибору центру приведення. Інваріанти системи. Теореми Варіньйона. Лекція 8. Додавання паралельних сил. Центр паралельних сил. Центр тяжіння. Визначення положення центру тяжіння однорідних тіл. Центри тяжіння найпростіших фігур. Способи визначення положення центрів тяжіння. ЛІТЕРАТУРА1. Теоретична механіка : Теретична механіка та опір матеріалів: підруч. для студ. вищ. навч. закл. / А.І. Аркуша- К. : Техніка, 2021. - 352 с. ISBN 978-5-9710-8544-72. Теоретична механіка : збірник задач: навч. посібник для студ. вищих навч. закл. / А. І. Федуліна- К. : Вищи школа, 2005. - 319 с.

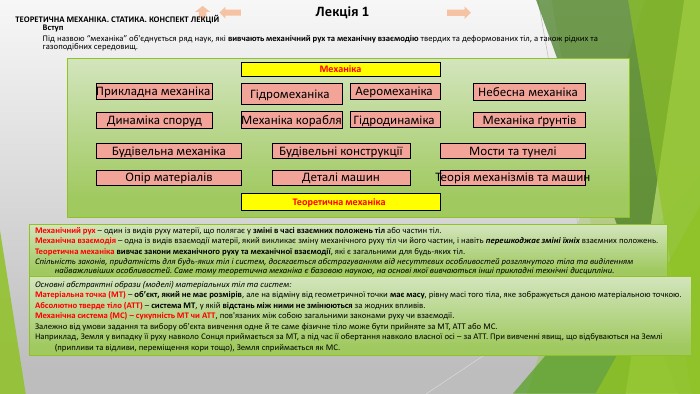
Вступ. Під назвою “механіка” об'єднується ряд наук, які вивчають механічний рух та механічну взаємодію твердих та деформованих тіл, а також рідких та газоподібних середовищ. Механіка. Прикладна механіка Гідромеханіка Аеромеханіка Небесна механіка Динаміка споруд. Механіка корабля. Основні абстрактні образи (моделі) матеріальних тіл та систем: Матеріальна точка (МТ) – об’єкт, який не має розмірів, але на відміну від геометричної точки має масу, рівну масі того тіла, яке зображується даною матеріальною точкою. Абсолютно тверде тіло (АТТ) – система МТ, у якій відстань між ними не змінюються за жодних впливів. Механічна система (МС) – сукупність МТ чи АТТ, пов'язаних між собою загальними законами руху чи взаємодії. Залежно від умови задання та вибору об'єкта вивчення одне й те саме фізичне тіло може бути прийняте за МТ, АТТ або МС. Наприклад, Земля у випадку її руху навколо Сонця приймається за МТ, а під час її обертання навколо власної осі – за АТТ. При вивченні явищ, що відбуваються на Землі (припливи та відливи, переміщення кори тощо), Земля сприймається як МС. Гідродинаміка Механіка ґрунтів. Будівельна механіка. Будівельні конструкціїМости та тунеліОпір матеріалів. Деталі машин. Теорія механізмів та машин. Теоретична механіка Механічний рух – один із видів руху матерії, що полягає у зміні в часі взаємних положень тіл або частин тіл. Механічна взаємодія – одна із видів взаємодії матерії, який викликає зміну механічного руху тіл чи його частин, і навіть перешкоджає зміні їхніх взаємних положень. Теоретична механіка вивчає закони механічного руху та механічної взаємодії, які є загальними для будь-яких тіл. Спільність законів, придатність для будь-яких тіл і систем, досягається абстрагуванням від несуттєвих особливостей розглянутого тіла та виділенням найважливіших особливостей. Саме тому теоретична механіка є базовою наукою, на основі якої вивчаються інші прикладні технічні дисципліни. Лекція 1 ТЕОРЕТИЧНА МЕХАНІКА. СТАТИКА. КОНСПЕКТ ЛЕКЦІЙ

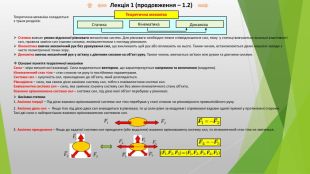
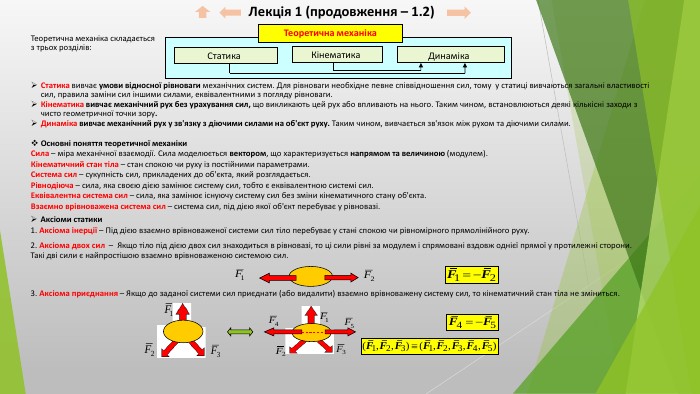
Лекція 1 (продовження – 1.2)Теоретична механіка складаєтьсяз трьох розділів: Статика вивчає умови відносної рівноваги механічних систем. Для рівноваги необхідне певне співвідношення сил, тому у статиці вивчаються загальні властивості сил, правила заміни сил іншими силами, еквівалентними з погляду рівноваги. Кінематика вивчає механічний рух без урахування сил, що викликають цей рух або впливають на нього. Таким чином, встановлюються деякі кількісні заходи з чисто геометричної точки зору. Динаміка вивчає механічний рух у зв'язку з діючими силами на об'єкт руху. Таким чином, вивчається зв'язок між рухом та діючими силами. Основні поняття теоретичної механіки. Сила – міра механічної взаємодії. Сила моделюється вектором, що характеризується напрямом та величиною (модулем). Кінематичний стан тіла – стан спокою чи руху із постійними параметрами. Система сил – сукупність сил, прикладених до об'єкта, який розглядається. Рівнодіюча – сила, яка своєю дією замінює систему сил, тобто є еквівалентною системі сил. Еквівалентна система сил – сила, яка замінює існуючу систему сил без зміни кінематичного стану об'єкта. Взаємно врівноважена система сил – система сил, під дією якої об'єкт перебуває у рівновазі. Аксіоми статики1. Аксіома інерції – Під дією взаємно врівноваженої системи сил тіло перебуває у стані спокою чи рівномірного прямолінійного руху.2. Аксіома двох сил – Якщо тіло під дією двох сил знаходиться в рівновазі, то ці сили рівні за модулем і спрямовані вздовж однієї прямої у протилежні сторони. Такі дві сили є найпростішою взаємно врівноваженою системою сил.3. Аксіома приєднання – Якщо до заданої системи сил приєднати (або видалити) взаємно врівноважену систему сил, то кінематичний стан тіла не зміниться. Статика Кінематика Теоретична механіка. Динаміка

Аксіоми статики (продовження)Наслідок із аксіоми приєднання – Кінематичний стан тіла не зміниться, якщо силу перенести вздовж лінії її дії.4 . Аксіома про паралелограм сил – рівнодіюча двох сил, що перетинаються, дорівнює діагоналі паралелограма, побудованого на цих силах як на сторонах.5. Аксіома дії та протидії – Будь-якій дії відповідає рівна за величиною та протилежна за напрямком протидія (III закон Ньютона).6. Аксіома затвердіння - Рівновага деформованого тіла зберігається у разі його затвердіння (обернене твердження справедливе не завжди). В’язі та реакції в’язей. Вільне тіло – це тіло, свобода переміщень якого не обмежується жодними іншими тілами. Невільне тіло – це тіло, рух якого обмежений іншими тілами. В’язь – тіло, що обмежує свободу переміщень об'єкта. Реакція в’язі – сила, що діє на об'єкт із боку в’язі. Принцип звільнення від в’язей – невільне тіло можна розглядати як вільне, якщо відкинути в'язі і замінити їхню дію відповідними реакціями. Лекція 1 (продовження – 1.3)

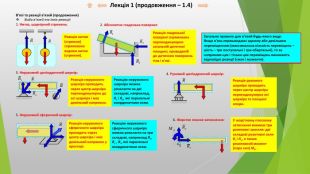
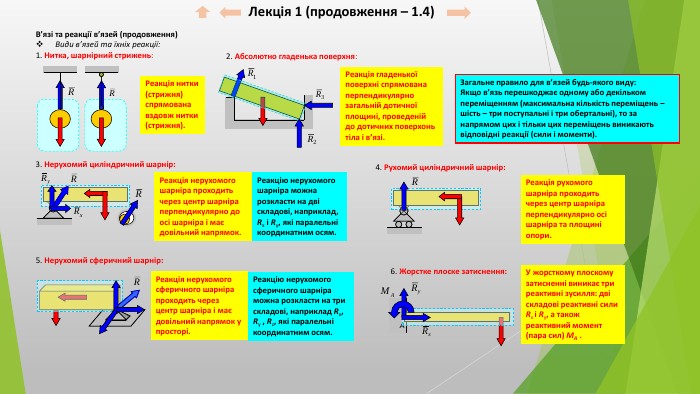
Лекція 1 (продовження – 1.4)В’язі та реакції в’язей (продовження)Види в’язей та їхніх реакції:1. Нитка, шарнірний стрижень:2. Абсолютно гладенька поверхня: Реакція нитки(стрижня)спрямованавздовж нитки(стрижня). Реакція гладенької поверхні спрямована перпендикулярно загальній дотичної площині, проведеній до дотичних поверхонь тіла і в’язі.3. Нерухомий циліндричний шарнір: Реакція нерухомого шарніра проходить через центр шарніра перпендикулярно до осі шарніра і має довільний напрямок. Реакцію нерухомого шарніра можна розкласти на дві складові, наприклад, Rx і Rу, які паралельні координатним осям.4. Рухомий циліндричний шарнір: Реакція рухомого шарніра проходить через центр шарніра перпендикулярно осі шарніра та площині опори.5. Нерухомий сферичний шарнір: Реакція нерухомого сферичного шарніра проходить через центр шарніра і має довільний напрямок у просторі. Реакцію нерухомого сферичного шарніра можна розкласти на три складові, наприклад Rx, Rу , Rz, які паралельні координатним осям.6. Жорстке плоске затиснення: AУ жорсткому плоскому затисненні виникає три реактивні зусилля: дві складові реактивні сили Rx і Rу, а також реактивний момент (пара сил) MA . Загальне правило для в’язей будь-якого виду: Якщо в’язь перешкоджає одному або декільком переміщенням (максимальна кількість переміщень – шість – три поступальні і три обертальні), то за напрямом цих і тільки цих переміщень виникають відповідні реакції (сили і моменти).

Лекція 2 Система збіжних сил – система, у якій лінії дії сил перетинаються в одній точці. План дослідження будь-якої системи сил відповідає послідовному розв’язанні трьох питань: Як спростити систему?Який найпростіший вигляд системи?Які умови рівноваги системи?Перенесемо всі сили вздовж лінії їхньої дії в точку перетину (кінематичний стан тіла за цього не зміниться - слідство з аксіоми приєднання). Складемо перші дві сили F1 і F2 (аксіома про паралелограм сил). Кількість сил зменшилась на одиницю. Складемо отриману рівнодіючу R12 з наступною силою F3. Кількість сил знову зменшилась на одиницю. Повторимо цю операцію з наступною силою F4. Залишилась лише одна сила, еквівалентна вихідній системі сил. Складання сил побудовою паралелограмів можна замінити побудовою силового трикутника (багатокутника) – обирається одна з сил або зображується паралельно самій собі з початком у будь-якій довільній точці, всі інші сили зображуються паралельними самим собі з початком, що збігається з кінцем попередньої сили.2. Найпростіший вигляд системи – сила, прикладена у точці перетину вихідних сил. Таким чином, схожа система сил приводиться до однієї сили – рівнодіючої (сили, еквівалентної вихідній системі сил), що дорівнює геометричній сумі сил системи. Якщо рівнодіюча система виявляється не рівною нулю, то під дією такої системи сил тіло буде рухатися в напрямку рівнодіючої (система сил не врівноважена). Для того, щоб урівноважити систему, достатньо прикласти силу, рівну отриманій рівнодіючій і спрямованій у протилежний бік (аксіома про дві сили). Таким чином, умовою рівноваги збіжної системи сил є рівність рівнодіючої нулю. Ця умова є еквівалентною замкнутості силового багатокутника певним чином, а саме, напрямок всіх сил при обході за контуром не змінюється за напрямком: Результатом такого складання є вектор, спрямований з початку першої сили до кінця останньої.style.colorfillcolorfill.typefill.on

Лекція 2 (продовження – 2.2)Теорема про три сили – Якщо під дією трьох непаралельних сил тіло знаходиться в рівновазі, то лінії дії цих сил перетинаються в одній точці. Перенесемо дві сили вздовж лінії їхньої дії в точку їх перетину (кінематичний стан тіла при цьому не зміниться - слідство з аксіоми приєднання). Складемо ці сили (аксіома про паралелограм сил). Тепер система складається з двох сил. А така система перебуває у рівновазі, якщо ці сили рівні між собою і спрямовані вздовж однієї лінії у протилежні сторони. Таким чином, усі три сили перетинаються в одній точці. Теорема про три сили може ефективно застосовуватися для визначення напрямку однієї з двох реакцій тіл: Реакція рухомого шарніра RB спрямована вертикально (перпендикулярно опорній площині). Напрямок (кут нахилу до горизонту) реакції нерухомого шарніра RА поки що не визначено. Якщо тіло під дією трьох сил F, RA и RB знаходиться в рівновазі,то всі три сили повинні перетинатися в одній точці (у точці С) : Дійсні напрямки та величини реакцій легко визначаються побудовою силового трикутника та використанням подібності трикутників : Аналітичне визначення рівнодіючої – Кожна із сил, геометрична сума яких дає рівнодіючу, може бути представлена ​​через її проекції на координатні вісі та одиничні вектори (орти): Тоді рівнодіюча виражається через проекції сил наступним чином: Групування за ортами дає вирази для проекцій рівнодіючої : Звідси проекціїрівнодіючої : Модуль рівнодіючої : Напрямні косинусирівнодіючої : Звідсирівняннярівноваги:style.colorfillcolorfill.typefill.on

Лекція 3 Плоска довільна система сил – система, в якій сили лежать в одній площині та їхні лінії дії не перетинаються в одній точці. Для розгляду такої системи сил необхідно ввести нові поняття: Момент сили відносно точки на площині. Пара сил. Момент пари сил. Момент сили відносно точки на площині – алгебраїчна величина, що дорівнює добутку модуля сили на плече, взята зі знаком «+» (плюс), якщо обертання площини під дією сили відбувається проти годинникової стрілки, і зі знаком «–» (мінус) в протилежному випадку. Плече сили – довжина перпендикуляра, проведеного з точки на лінію дії сили. Пара сил – сукупність двох паралельних одна одній сил, рівних за величиною та спрямованих у протилежні сторони. Пара сил не може бути спрощена (не може бути замінена однією силою) і є новою силовою характеристикою механічної взаємодії. Момент пари сил на площині (теорема про момент пари сил) не залежить від вибору центру приведення (полюса) і дорівнює добутку модуля будь-якої з сил пари на плече пари, взятим зі знаком «+» (плюс), якщо обертання площини під дією пари сил відбувається проти годинникової стрілки, і зі знаком «–» (мінус) в протилежному випадку. Плече пари сил – довжина перпендикуляра, проведеного з будь-якої точки на лінії дії однієї із сил пари на лінію дії іншої сили цієї пари. AAУ незалежності моменту пари та від вибору полюса можна переконатися обчисленням суми моментів від кожної з сил відносно будь-якого центру. Теореми про пари : Про перенесення пари сил у площині її дії – Пару сил можна перенести у будь-яке місце у площині її дії. Кінематичний стан тіла не зміниться. Про еквівалентність пар сил – Пару сил можна замінити іншою парою сил, якщо їхні моменти алгебраїчно рівні. Кінематичний стан тіла не зміниться. Про складання пар сил на площині – Систему пар сил на площині можна замінити однією парою, момент якої дорівнює алгебраїчній сумі моментів вихідних пар. Кінематичний стан тіла не зміниться. Умова рівноваги системи пар сил

Лекція 3 (продовження – 3.2)AДодамо до системи в точці A дві сили, рівні за величиною між собою та з величиною заданої сили, спрямовані вздовж однієї прямої у протилежні сторони та паралельні заданій силі: Кінематичний стан не змінився (аксіома про приєднання). Вихідна сила та одна з доданих сил утворюють пару сил. Момент цієї пари чисельно дорівнює моменту вихідної сили відносно центру приведення. У багатьох випадках пару сил зручно зображати дуговою стрілкою. AЗбіжна система сил приводиться до однієї сили, прикладеної в центрі приведення, яка раніше називалася рівнодіючою, але тепер ця сила не замінює вихідну систему сил, оскільки після приведення виникла система пар. Система пар приводиться до однієї пари (теорема про складання пар), момент якої дорівнює алгебраїчній сумі моментів вихідних сил відносно центру приведення. AУ загальному випадку плоска довільна система сил приводиться до однієї сили, яка називається головним вектором і до пари з моментом, рівним головному моменту всіх сил системи відносно центру приведення: - головний вектор, - головний момент. Умовою рівноваги плоскої довільної системи сил є одночасна рівність головного вектора та головного момента системи нулю: Рівняння рівноваги (I форма) маємо у вигляді системи трьох рівнянь із умов рівноваги з використанням виразів для проекцій головного вектора:Існують ще дві форми рівнянь рівноваги (II та III форми) : Приведення сили до заданого центру (метод Пуансо) – силу можна перенести паралельно самій собі в будь-яку точку площини, якщо додати відповідну пару сил, момент якої дорівнює моменту цієї сили відносно точки, що розглядається. Приведення плоскої довільної системи сил до заданого центру. Вибираємо довільну точку на площині і кожну з сил переносимо методом Пуансо в цю точку. Замість вихідної довільної системи отримаємо схожу систему сил і систему пар.style.colorfillcolorfill.typefill.onstyle.colorfillcolorfill.typefill.onstyle.colorfillcolorfill.typefill.on

Лекція 3 (продовження – 3.3)Слід звернути увагу на те, що ІІ та ІІІ форми рівнянь рівноваги мають обмеження, пов'язані з вибором однієї з осей, наприклад, осі x і точки С відносно положення точок A і B. Обмеження, що накладаються на вибір осі x (не перпендикулярно AB) та точки C (не лежить на AB),гарантують, що жодне з рівнянь не є тотожністю при виконанні двох інших рівнянь. Теорема Варіньйона про момент рівнодіючої. Якщо система сил має рівнодіючу, то момент цієї рівнодіючої відносно будь-якого центру дорівнює алгебраїчній сумі моментів сил системи відносно того ж центру. Доказ: Нехай система сил F1, F2, F3 … приводиться до рівнодіючої, прикладеної у точці O. AOТака система не перебуває у рівновазі (R ≠ 0). Урівноважимо цю систему силою R’, рівною рівнодіючій R, спрямованій вздовж лінії її дії у протилежний бік (аксіома про дві сили). Таким чином, система вихідних сил F1, F2, F3 … та врівноважуюча сила R’ знаходиться в рівновазі і повинна задовольняти рівнянням рівноваги, наприклад: Оскільки сила R’, дорівнює рівнодіючій R та спрямована вздовж лінії її дії у протилежний бік, то MA(R’) = –MA(R ). Підстановка цієї рівності до рівняння рівноваги дає : або Приклади використання теореми про момент рівнодіючої:1. Визначення моменту сили відносно точки, коли складно обчислювати плече сили. Наприклад: AСилу F розкладемо на складові F1 и F2. Тоді момент сили F відносно точки A можна обчислити як суму моментів кожної із сил відносно цієї точки:2. Доказ необхідності обмежень для ІІ та ІІІ форм рівнянь рівноваги: Якщо , то система приводиться до рівнодіючої, при цьому вона проходить через точку A, через те, що її момент відносно цієї точки має дорівнювати нулю (теорема Варіньйона). Якщо при цьому , то рівнодіюча повинна також проходити через точку B. ABТоді проекція рівнодіючої на вісь, перпендикулярну AB, і момент рівнодіючої відносно точки, що лежить на AB, будуть тотожно рівні нулю за будь-якого значення рівнодіючої. С

Лекція 4 Плоскі ферми – геометрично незмінні стрижневі конструкції, стрижні яких лежать в одній площині. Вузли ферми – точки, у яких сходяться вісі стрижнів (опорні вузли – вузли, якими ферма спирається на основу). Верхній та нижній пояси – стрижні, що утворюють верхній та нижній контури. Стійки – вертикальні стрижні. Розкоси – похилі стрижні. Прогін ферми – відстань між опорними вузлами (l). Довжина панелі – відстань між стійками (d). ABhld. Способи розрахунку. Для розрахунку зусиль, що виникають у стрижнях ферми, використовуютьсяметод вирізання вузлів та метод перерізів (метод Ріттера). Основні припущення, прийняті під час розрахунку ферм: Всі вузли з'єднання стрижнів вважаються ідеальними шарнірами, що не перешкоджають взаємному повороту стрижнів. Вузли у металевих фермах, у яких стрижні з'єднуються за допомогою фасонних листів та заклепок, також розглядаються як шарнірні, оскільки при навантаженні вони допускають малі пружні деформації (взаємні повороти).2. Навантаження прикладається у вузлах. Для вузлової передачі навантаження практично використовуються спеціальні балочні конструкції.3. Геометричні розміри ферми не змінюються під час навантаження (деформації малі). Метод вирізання вузлів. Послідовно вирізаються вузли ферми так, щоб у двох рівняннях рівноваги для кожного з вузлів було не більше двох невідомих зусиль. Як правило, зовнішні опорні реакції повинні бути попередньо визначені.2. Нумеруємо або позначаємо літерами позначені вузли. Реакції стрижнів (або зусилля в них) будемо позначати далі двома індексними цифрами або літерами – перша зних збігається з номером (позначенням) вузла, що вирізається, а друга вказує, до якого вузла приєднується іншим кінцем розглянутий стрижень.3. Вирізаємо вузол A (у цьому вузлі всього два невідомі зусилля) і замінюємо дію розрізаних(відкинутих) вузлів зусиллями (реакціями) SA1 і SA6.12345678 A4. Складаємо рівняння рівноваги для вузла A та обчислюємо зусилля SA1 і SA6.5. Вирізаємо вузол 1 (у цьому вузлі всього два невідомі зусилля) і замінюємо дію розрізаних (відкинутих) вузлів зусиллями (реакціями) S1 A, S12 і S16.16. Складаємо рівняння рівноваги для вузла 1 та обчислюємо зусилля S12 и S16 (S1 A и SA1 рівні алгебраїчно, оскільки при направленні невідомих зусиль від вузла аксіома дії та протидії виконується автоматично). Порядок розрахунку:1. Вибираємо як об'єкт рівноваги ферму в цілому та визначаємо опорні реакції : Далі процес вирізання вузлів тавизначення зусиль повторюється у певному порядку, наприклад :2, 6, 7, 3, 4, 8, 5. Вирізанням останнього вузла B можна контролювати правильність розрахунку.

Лекція 4 (продовження – 4.2)Метод вирізання вузлів для обчислення зусилля лише у зазначеному стрижні вимагає розгляду всіх вузлів та розв'язання для них рівнянь рівноваги (принаймні вузлів, що знаходяться між одним із опорних вузлів та вузлом, до якого підходить зазначений стрижень). Крім того, послідовне обчислення зусиль та підстановка результатів у подальший розрахунок при великій кількості вузлів загрожує накопиченням помилок, не кажучи вже про те, допущена груба помилка в одному з вузлів робить подальші обчислення невірними. Метод перерізів (метод Ріттера) у більшості випадків не вимагає для обчислення зусилля лише у зазначеному стрижні складання будь-яких інших допоміжних рівнянь рівноваги, крім того рівняння, в якому безпосередньо бере участь необхідне зусилля. Метод ґрунтується на складанні одного рівняння рівноваги з використанням II та III форм рівнянь рівноваги довільної плоскої системи сил. Порядок розрахунку:1. Вибираємо як об'єкт рівноваги ферму в цілому та визначаємо опорні реакції: ABhld123456782. Проводимо наскрізний переріз, що поділяє ферму на дві частини так, щоб у переріз потрапляло не більше трьох стрижнів, в одному з яких потрібно знайти зусилля, наприклад, переріз I-I для визначення S23. II3. Вибираючи як об'єкт рівноваги одну частину, наприклад, праву, відкидаємо іншу (ліву) частину.4. Дію відкинутої частини замінюємо на реакції стрижнів, що потрапили у розріз – S32, S36 і S76.5. Для шуканого зусилля S32 знаходимо положення точки Ріттера, як точки перетину ліній дії двох інших зусиль S36 і S76, як точки перетину ліній дії двох інших зусиль. Точка Ріттера для зусилля S32 збігається з вузлом 6.6. Складаємо моментне рівняння рівноваги для правої частини відносно знайденої точки Ріттера (вузла 6) та визначаємо шукане зусилля.7. Для визначення зусилля S76 знаходимо положення точки Ріттера, як точки перетину ліній дії двох інших зусиль S36 і S32, які не підлягають визначенню на даний момент. Точка Ріттера для зусилля S76 збігається з вузлом 3.8. Складаємо моментне рівняння рівноваги для правої частини відносно знайденої точки Ріттера (вузла 3) та визначаємо шукане зусилля.9. При визначенні зусилля S36 , точка Ріттера, як точка перетину ліній дії двох інших зусиль S76 і S32, які не підлягають визначенню в даний момент, йде в нескінченність (S76 і S32 є паралельними). У цьому випадку моментне рівняння рівноваги перетворюється на рівняння рівноваги в проекціях на вісь, перпендикулярну лініям, що йдуть у нескінченність. Для визначення інших зусиль необхідно провести інший переріз (пункт 2) та повторити описані дії (пункти 3, 4 і далі)style.colorfillcolorstroke.colorfill.typestyle.colorfillcolorstroke.colorfill.type

Лекція 4 (продовження – 4.3)Рівновага зчленованих тіл. Залізничні та будівельні конструкції можуть складатися із зчленованих між собою тіл (балок, ферм). Кількість накладених в'язей може перевищувати кількість незалежних рівнянь рівноваги, які можна скласти для розглянутої конструкції. Такі задачі є статично невизначуваними. Ступінь статичної невизначуваності для плоских систем дорівнює:де Д – кількість жорстких дисків, Ж – кількість жорстких затиснень, Ш – число нерухомих шарнірів (опорних та тих, що сполучають диски між собою), С – число шарнірних стрижнів (опорних та тих, що сполучають диски між собою) або рухомих шарнірів AB1. Виберемо як об'єкт всю конструкцію. СBУ теоретичній механіці можливе розв'язання лише статично визначуваних задач, у яких кількість в'язей дорівнює числу незалежних рівнянь рівноваги (n = 0).2. Відкинемо в'язі та замінимо їхню дію реакціями.3. Число невідомих реакцій – 4, а кількість незалежних рівнянь – 3. Це означає, що необхідно розчленувати конструкцію – відкинути шарнір C та замінити його дію на кожну з частин реакціями.4. Розв’язання отриманої системи рівнянь не представляє особливих труднощів у зазначеному порядку: спочатку допоміжна балка CB (не може залишатися у рівновазі без балки AC), потім основна балка AC (може бути у рівновазі без балки CB). Рівновага важеля. Важіль – тверде тіло, що має одну нерухому точку. Важіль має один ступінь кінематичної рухливості (w = – n = 3 Д – 3 Ж – 2 Ш – С = 3·1 – 3·0 – 2·1 – 0 = 1) і в рівновазі може бути лише за певного співвідношення активних сил, що діють на важіль. AРівняння рівноваги важеля. Застосовуючи загальний підхід до складання рівнянь рівноваги для важеля отримаємо: У багатьох випадках значення опорних реакцій не є важливими і шукане співвідношення сил визначають з останнього моментного рівняння, яке і приймається за рівняння рівноваги важеля. Рівняння рівноваги важеля використовується за розрахунку підпірної стінки або вантажу на перекидання: AУмова стійкості на перекидання: Утримуючий момент відносно нерухомої точки (від F1) повинен бути більше перекидального моменту (від F2) відносно цієї точки.

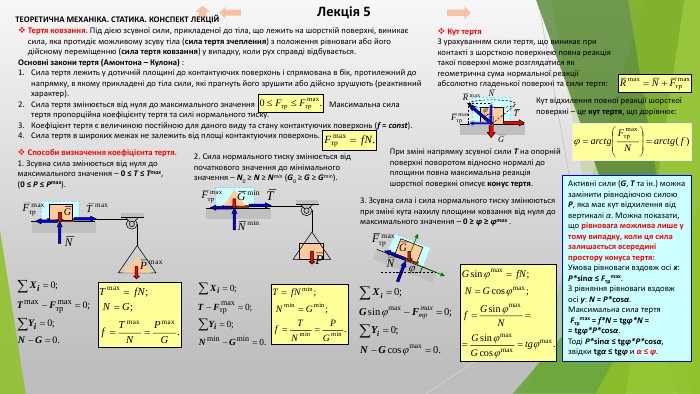
Лекція 5 ТЕОРЕТИЧНА МЕХАНІКА. СТАТИКА. КОНСПЕКТ ЛЕКЦІЙТертя ковзання. Під дією зсувної сили, прикладеної до тіла, що лежить на шорсткій поверхні, виникає сила, яка протидіє можливому зсуву тіла (сила тертя зчеплення) з положення рівноваги або його дійсному переміщенню (сила тертя ковзання) у випадку, коли рух справді відбувається. Основні закони тертя (Амонтона – Кулона) : Сила тертя лежить у дотичній площині до контактуючих поверхонь і спрямована в бік, протилежний до напрямку, в якому прикладені до тіла сили, які прагнуть його зрушити або дійсно зрушують (реактивний характер). Сила тертя змінюється від нуля до максимального значення Максимальна сила тертя пропорційна коефіцієнту тертя та силі нормального тиску. Коефіцієнт тертя є величиною постійною для даного виду та стану контактуючих поверхонь (f = const). Сила тертя в широких межах не залежить від площі контактуючих поверхонь. Способи визначення коефіцієнта тертя.1. Зсувна сила змінюється від нуля до максимального значення – 0 ≤ T ≤ Tmax, (0 ≤ P ≤ Pmax).2. Сила нормального тиску змінюється від початкового значення до мінімального значення – N0 ≥ N ≥ Nmin (G0 ≥ G ≥ Gmin).3. Зсувна сила і сила нормального тиску змінюються при зміні кута нахилу площини ковзання від нуля до максимального значення – 0 ≥ φ ≥ φmax . Кут тертя. З урахуванням сили тертя, що виникає при контакті з шорсткою поверхнею повна реакція такої поверхні може розглядатися як геометрична сума нормальної реакції абсолютно гладенької поверхні та сили тертя: Кут відхилення повної реакції шорсткої поверхні – це кут тертя, що дорівнює: При зміні напрямку зсувної сили T на опорній поверхні поворотом відносно нормалі до площини повна максимальна реакція шорсткої поверхні описує конус тертя. Активні сили (G, T та ін.) можна замінити рівнодіючою силою P, яка має кут відхилення від вертикалі α. Можна показати, що рівновага можлива лише у тому випадку, коли ця сила залишається всередині простору конуса тертя: Умова рівноваги вздовж осі x: P*sinα ≤ Fтрmax. З рівняння рівноваги вздовж осі у: N = P*cosα. Максимальна сила тертя Fтрmax = f*N = tgφ*N == tgφ*P*cosα. Тоді P*sinα ≤ tgφ*P*cosα, звідки tgα ≤ tgφ и α ≤ φ.

Лекція 5 (продовження – 5.2)Урахування сил тертя під час розв’язання задач на рівновагу. За наявності сил тертя: До діючих на об'єкт активних сил і реакцій абсолютно гладеньких поверхонь додаються відповідні сили тертя, спрямовані вздовж загальної дотичної до контактуючих поверхонь у бік, протилежний можливому зміщенню точки торкання об'єкта відносно опорної шорсткої площини. До рівнянь рівноваги, складених для об'єкта, додаються вирази для максимальних сил тертя в кількості, що дорівнює кількості сил тертя. Приклад розв'язання задачі на рівновагу з урахуванням сил тертя. Людина вагою G збирається встановити легку драбину під кутом α до вертикалі (стіни) і піднятися на половину довжини драбини для виконання роботи. Коефіцієнти тертя в точках контакту драбини із підлогою (A) та зі стіною (B) рівні f. A і f. B відповідно. Визначити граничне значення кута нахилу, у якому драбина з людиною можуть зберігати рівновагу. Вагою драбини знехтувати.1. Вибираємо об'єкт (людина та драбина), відкидаємо в'язі та замінюємо їхню дію реакціями гладенької поверхні. AB2. Додаємо активні сили (силу тяжіння G). Драбина легка, її вагою нехтуємо.3. Додаємо сили тертя, спрямовані у бік, протилежний до можливого переміщення контактних точок A і B драбини під дією доданої активної сили.4. Складаєморівняннярівноваги :5. Додаємо вирази для сил тертя:7. Розв`язання перших двох рівнянь дає виразидля нормальних реакцій:8. Підстановка виразів для нормальних реакцій у третє рівняння рівноваги призводить до можливості визначення граничного кута нахилу α: ABВизначення області рівноваги. Задачу розв’язано для конкретного положення людини, а кут нахилу відповідає граничній рівновазі (використані максимальні значення сил тертя). За допомогою поняття конуса тертя, що утворюється повною реакцією шорсткої поверхні, та теореми про три сили можна визначити область можливих рівноважних положень людини на сходах. Для цього достатньо за заданими коефіцієнтами тертя визначити кути тертя, що задають граничні положення повної реакції та побудувати конуси тертя. Спільна область конусів дає область рівноважних положень людини. Добре видно, що для більш високого положення людини треба зменшувати кут нахилу.6. Підстановка виразів з пункту 5 в рівняння рівноваги з простими перетвореннями третього рівняння дає:

Основні закони тертя кочення:1. Момент опору коченню завжди спрямований у протилежний бік до того напрямку, в якому прикладені до тіла сили, що прагнуть його повернути, або дійсному повороту під дією цих сил (реактивний характер).2. Момент опору коченню змінюється від нуля до максимального значення. Максимальний момент опору коченню пропорційний коефіцієнту тертя кочення та силі нормального тиску.3. Коефіцієнт тертя кочення – це постійна величина дляданого виду та стану контактуючих поверхонь (fк = const).4. Момент опору коченню у широких межах не залежить від радіуса котка. Опір під час кочення. Під дією сили зсуву, прикладеної до котка, що лежить на шорсткій поверхні, виникає сила, яка протидіє можливому зміщенню тіла (сила тертя зчеплення) з рівноважного положення або його дійсному переміщенню (сила тертя ковзання) за його руху і пара сил, момент якої перешкоджає повороту катка (момент опору коченню). Виникнення пари сил, яка перешкоджає коченню, пов'язано з деформацією опорної площини, внаслідок якої рівнодіюча нормальних реактивних сил вздовж площадки контакту зміщена від лінії дії сили тяжіння у бік можливого або дійсного руху. Якщо коефіцієнт тертя ковзання є безрозмірною величиною, то коефіцієнт тертя кочення вимірюється одиницями довжини тадорівнює за величиною зазначеному зміщенню рівнодіючої нормального тиску. Внаслідок деформації коефіцієнт тертякочення має дуже малу величину і становить, наприклад, для сталевого колеса на сталевій рейці 0,0005 м. Лекція 5 (продовження – 5.3)

Лекція 6 Просторова довільна система сил – система, в якій сили не лежать у одній площині та його лінії дії не перетинаються відносно однієї точки. Для розгляду такої системи сил необхідно ввести нові поняття: Момент сили відносно центру у просторі. Момент сили відносно вісі. Момент пари сил у просторі. Момент сили відносно центру у просторі – це векторна величина, яка дорівнює векторному добутку радіус-вектора, проведеного з центру до точки прикладання сили, та вектора сили. За визначенням векторного добутку вектор моменту сили спрямований перпендикулярно до площини, проведеної через центр і силу,у той бік, звідки поворот радіус-вектора до вектора сили на найменший кут видно таким, що відбувається за годинниковою стрілкою. Модуль вектора моменту сили відносно центру дорівнює : Модуль вектора моменту сили відносно центру чисельно дорівнює подвоєній площітрикутника OAB. Момент сили відносно вісі – алгебраїчна величина, яка дорівнює добутку проекції вектора сили на площину, перпендикулярну до осі, на плече цієї проекції відносно точки перетину вісі з площиною, взята зі знаком «+» (плюс), якщо обертання площини під дією сили видно при погляді назустріч осі таким, що відбувається проти годинникової стрілки, і зі знаком «–» (мінус) в протилежному випадку. Момент сили відносно вісі чисельно дорівнює подвоєній площі трикутника Oab. Зв'язок моменту сили відносно центру та відносно вісі. Модуль вектора моменту сили відносно центру, що лежить на вісі z, дорівнює подвоєній площі трикутника OAB: Момент сили відносно вісі z, дорівнює подвоєній площі трикутника Oab: Трикутник Oab отримано проекцією трикутника OAB на площину, перпендикулярну вісі z, та його площа пов'язана з площею трикутника OAB співвідношенням:де  - двогранний кут між площинами трикутників. Оскільки вектор моменту сили відносно точки перпендикулярний площині трикутника OAB, то кут між вектором і віссю дорівнює куту . Таким чином, момент сили відносно вісі є проекція вектора моменту сили відносно центру на цю вісь :

Лекція 6 (продовження – 6.2)Момент пари сил у просторі – вектор, перпендикулярний площині дії пари, спрямований у той бік, звідки обертання площини під дією пари видно таким, що відбувається проти годинникової стрілки. Модуль вектора моменту пари дорівнює добутку однієї з сил пари на плече пари : Теореми про пари: (Теореми наводяться без доказів) Про перенесення пари сил у площину, паралельну площині її дії – Пару сил можна перенести у будь-яку площину, паралельну площині її дії. Кінематичний стан тіла не зміниться. Про еквівалентність пар сил – Пару сил можна замінити іншою парою сил, якщо їхні моменти геометрично (векторно) рівні. Кінематичний стан тіла не зміниться. Про складання пар сил на площині – Систему пар сил на площині можна замінити однією парою, момент якої дорівнює геометричній (векторній) сумі моментів вихідних пар. Кінематичний стан тіла не зміниться. Умова рівноваги системи пар сил Далі будемо дотримуватися загального плану дослідження системи сил, послідовно вирішуючи три питання :1. Як спростити систему?2. Який найпростіший вигляд системи?3. Які умови рівноваги системи?Приведення плоскої довільної системи сил до заданого центру – вибираємо довільну точку на площині і кожну з сил переносимо методом Пуансо в цю точку. Замість вихідної довільної системи отримаємо схожу систему сил і систему пар. На відміну від раніше розглянутої плоскої довільної системи сил, тепер при використанні методу Пуансо приєднані пари сил характеризуються векторами. AЗбіжна система сил приводиться до однієї сили, прикладеної в центрі приведення. Система пар приводиться до одної пари (теорема про складання пар), момент якої дорівнює векторній сумі моментів вихідних сил відносно центру приведення. AУ загальному випадку плоска довільна система сил приводиться до однієї сили, яка називається головним вектором і до пари з моментом, рівним головному моменту всіх сил системи відносно центру приведення. : - головний вектор, - головний момент. ТЕОРЕТИЧНА МЕХАНІКА. СТАТИКА. КОНСПЕКТ ЛЕКЦІЙ

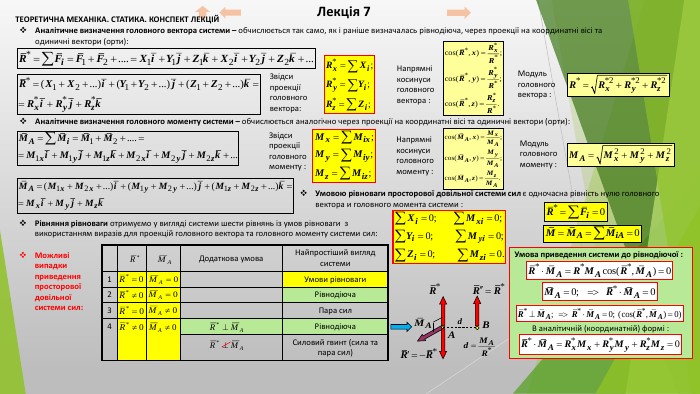
Лекція 7 Умовою рівноваги просторової довільної системи сил є одночасна рівність нулю головного вектора и головного момента системи : Рівняння рівноваги отримуємо у вигляді системи шести рівнянь із умов рівноваги з використанням виразів для проекцій головного вектора та головного моменту системи сил: Звідси проекціїголовного вектора: Модульголовного вектора : Напрямні косинусиголовного вектора : Аналітичне визначення головного моменту системи – обчислюється аналогічно через проекції на координатні вісі та одиничні вектори (орти): Звідсипроекціїголовного моменту : Модульголовного моменту : Напрямнікосинусиголовного моменту : Можливі випадки приведення просторової довільної системи сил: Додаткова умова. Найпростіший вигляд системи1 Умови рівноваги2 Рівнодіюча3 Пара сил4 Рівнодіюча. Силовий гвинт (сила та пара сил)Умова приведення системи до рівнодіючої : В аналітичній (координатній) формі : ТЕОРЕТИЧНА МЕХАНІКА. СТАТИКА. КОНСПЕКТ ЛЕКЦІЙАналітичне визначення головного вектора системи – обчислюється так само, як і раніше визначалась рівнодіюча, через проекції на координатні вісі та одиничні вектори (орти):

Головний момент не є інваріантом, оскільки залежить від вибору центру приведення. Однак існує величина, пов'язана з головним вектором, яка не залежить від вибору центру приведення :1. Запишемо залежність для основного моменту системи від вибору точки приведення: Лекція 7 (продовження – 7.2)Інваріанти системи сил – величини, які не залежать від вибору центру приведення: Перший (векторний) інваріант – головний вектор системи сил R*:2. Помножимо ліву та праву частини цього виразу скалярно на головний вектор та розкриємо дужки :3. Другий добуток у правій частині дорівнює нулю через те, що головний вектор R* перпендикулярний вектору векторного добутку в дужках. Звідси отримуємо тотожність: Таким чином, скалярний добуток головного вектора R* на вектор головного моменту MA є другим (скалярним) інваріантом : Звідси, головний мінімальний момент M* також є інваріантною величиною : Теореми Варіньйона про моменти рівнодіючої для просторової системи сил : Якщо система сил має рівнодіючу, томомент рівнодіючої відносно будь-якого центру дорівнює геометричній сумі моментів сил системи відносно того ж центру;момент рівнодіючої відносно будь-якої вісі дорівнює алгебраїчній сумі моментів сил системи відносно тієї ж вісі. Доказ: Нехай система сил F1, F2, F3 … приводиться до рівнодіючої, прикладеної в точці O. Така система не перебуває у рівновазі (R ≠ 0). AOУрівноважимо цю систему силою R’, рівною рівнодіючій R, направленій вздовж лінії її дії у протилежний бік (аксіома про дві сили). Система вихідних сил F1, F2, F3 … та врівноважуючої сили R’ знаходиться в рівновазі і має задовольняти умови рівноваги, наприклад : Оскільки сила R’ дорівнює рівнодіючій R та спрямована вздовж лінії її дії у протилежний бік, то MA(R’) = – MA(R). Підстановка цієї рівності до рівняння рівноваги дає: або Cпроектуємо цю векторну рівність на будь-яку вісь, наприклад, x: ТЕОРЕТИЧНА МЕХАНІКА. СТАТИКА. КОНСПЕКТ ЛЕКЦІЙ

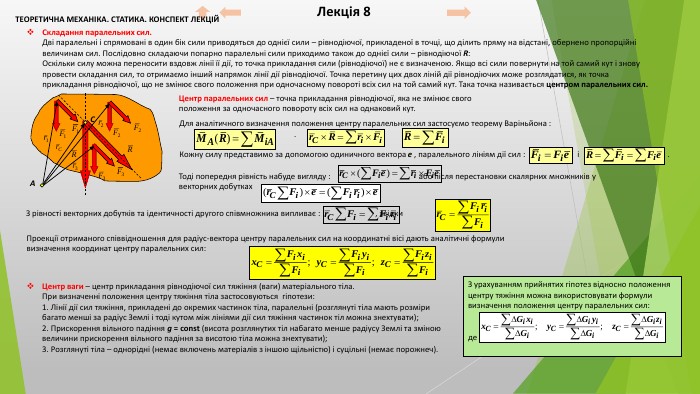
Для аналітичного визначення положення центру паралельних сил застосуємо теорему Варіньйона : або . Лекція 8 Складання паралельних сил. Дві паралельні і спрямовані в один бік сили приводяться до однієї сили – рівнодіючої, прикладеної в точці, що ділить пряму на відстані, обернено пропорційні величинам сил. Послідовно складаючи попарно паралельні сили приходимо також до однієї сили – рівнодіючої R: Оскільки силу можна переносити вздовж лінії її дії, то точка прикладання сили (рівнодіючої) не є визначеною. Якщо всі сили повернути на той самий кут і знову провести складання сил, то отримаємо інший напрямок лінії дії рівнодіючої. Точка перетину цих двох ліній дії рівнодіючих може розглядатися, як точка прикладання рівнодіючої, що не змінює свого положення при одночасному повороті всіх сил на той самий кут. Така точка називається центром паралельних сил. Центр паралельних сил – точка прикладання рівнодіючої, яка не змінює свого положення за одночасного повороту всіх сил на однаковий кут. СAКожну силу представимо за допомогою одиничного вектора e , паралельного лініям дії сил : і . Тоді попередня рівність набуде вигляду : або після перестановки скалярних множників у векторних добутках. З рівності векторних добутків та ідентичності другого співмножника випливає : , звідки Проекції отриманого співвідношення для радіус-вектора центру паралельних сил на координатні вісі дають аналітичні формули визначення координат центру паралельних сил: Центр ваги – центр прикладання рівнодіючої сил тяжіння (ваги) матеріального тіла. При визначенні положення центру тяжіння тіла застосовуються гіпотези: 1. Лінії дії сил тяжіння, прикладені до окремих частинок тіла, паралельні (розглянуті тіла мають розміри багато менші за радіус Землі і тоді кутом між лініями дії сил тяжіння частинок тіл можна знехтувати); 2. Прискорення вільного падіння g = const (висота розглянутих тіл набагато менше радіусу Землі та зміною величини прискорення вільного падіння за висотою тіла можна знехтувати); 3. Розглянуті тіла – однорідні (немає включень матеріалів з іншою щільністю) і суцільні (немає порожнеч). З урахуванням прийнятих гіпотез відносно положення центру тяжіння можна використовувати формули визначення положення центру паралельних сил: де G – сили тяжіння елементарних об’ємів. ТЕОРЕТИЧНА МЕХАНІКА. СТАТИКА. КОНСПЕКТ ЛЕКЦІЙ

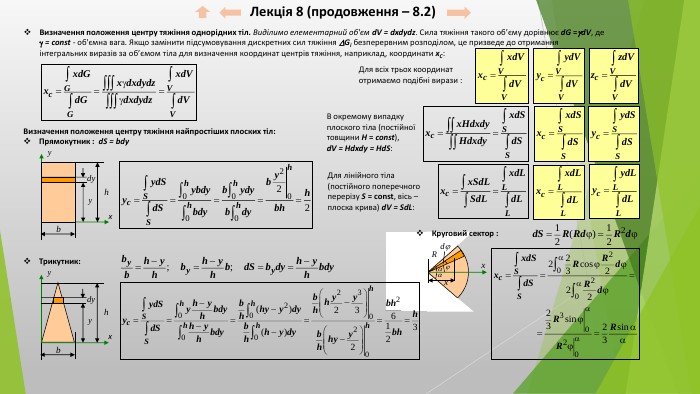
Лекція 8 (продовження – 8.2)Визначення положення центру тяжіння однорідних тіл. Виділимо елементарний об'єм d. V = dxdydz. Сила тяжіння такого об’єму дорівнює d. G =d. V, де  = const - об'ємна вага. Якщо замінити підсумовування дискретних сил тяжіння Gi безперервним розподілом, це призведе до отримання інтегральних виразів за об’ємом тіла для визначення координат центрів тяжіння, наприклад, координати x. C: В окремому випадку плоского тіла (постійної товщини H = const),d. V = Hdxdy = Hd. S: Для всіх трьох координат отримаємо подібні вирази : Для лінійного тіла (постійного поперечного перерізу S = const, вісь – плоска крива) d. V = Sd. L: Визначення положення центру тяжіння найпростіших плоских тіл: Прямокутник : d. S = bdyxx. Трикутник: Круговий сектор :

Лекція 8 (продовження – 8.3)Методи визначення положення центру ваги складних фігур 1. Метод розбиття – складна фігура розбивається на сукупність простих фігур, для яких відомі положення центру тяжіння або їх легко визначити:122. Метод негативних площ – так само, як і в методі розбиття, складна фігура розбивається на сукупність простих фігур, для яких відомі положення центру тяжіння або їх легко визначити, але за наявності отворів або пустот зручно їх представляти як “негативні” області. Наприклад, наступна фігура замість розбиття на 4 звичайні прямокутники, може бути представлена як сукупність двох прямокутників, один із яких має негативну площу:123. Метод симетрії – за наявності у фігури вісі чи площині симетрії центр ваги лежить на цій вісі чи в цій площини. З урахуванням цієї властивості зменшується кількість координат центру ваги, що підлягають визначенню. Як, наприклад, під час визначення положення центру ваги кругового сектора. Зауваження. Оскільки координата, наприклад, x2, може бути негативною, то не слід представляти цей вираз з використанням різниць : 4. Метод інтегрування – за наявності у фігури досить простого контуру, що описується відомим рівнянням (коло, парабола тощо), вибирається елементарний майданчик або смужка та виконується аналітичне інтегрування. Як, наприклад, під час визначення положення центру ваги трикутника або кругового сектора. За більш складного контуру, який може бути розбитий на простіші граничні відрізки, використовується попередньо метод розбиття. У разі складнощів з аналітичним інтегруванням використовуються чисельні методи інтегрування.5. Метод підвішування – експериментальний метод, заснований на тому, що під час підвішування тіла або фігури за будь-яку довільну точку центр ваги знаходиться на одній вертикалі з точкою підвішування. Для визначення положення центру тяжіння плоскої фігури достатньо підвісити її по черзі за дві будь-які точки і прокреслити відповідні вертикалі, наприклад, за допомогою інструментів (підвіс тощо), і точка перетину цих прямих відповідає положенню центру тяжіння фігури. ТЕОРЕТИЧНА МЕХАНІКА. СТАТИКА. КОНСПЕКТ ЛЕКЦІЙ