Презентація "Циліндр. Конус. Куля."
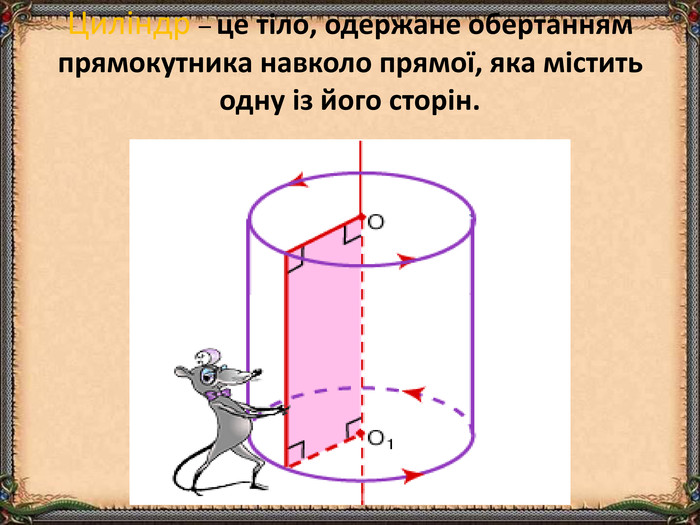
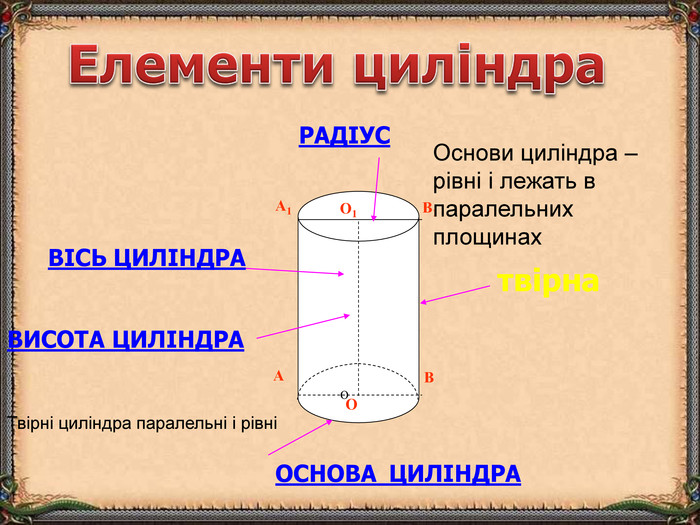
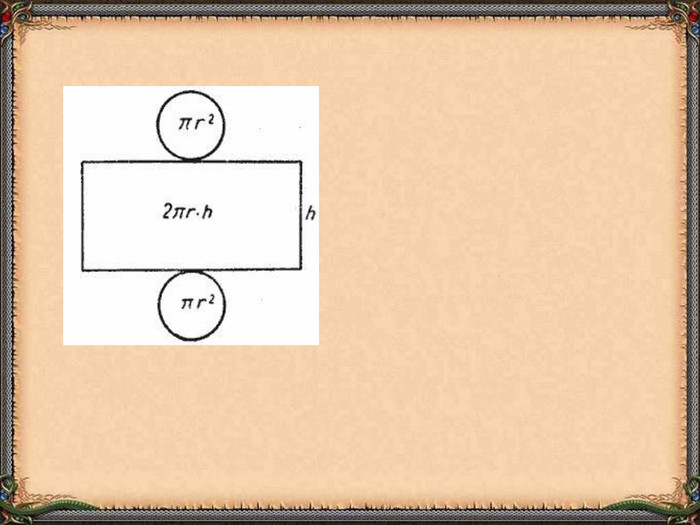
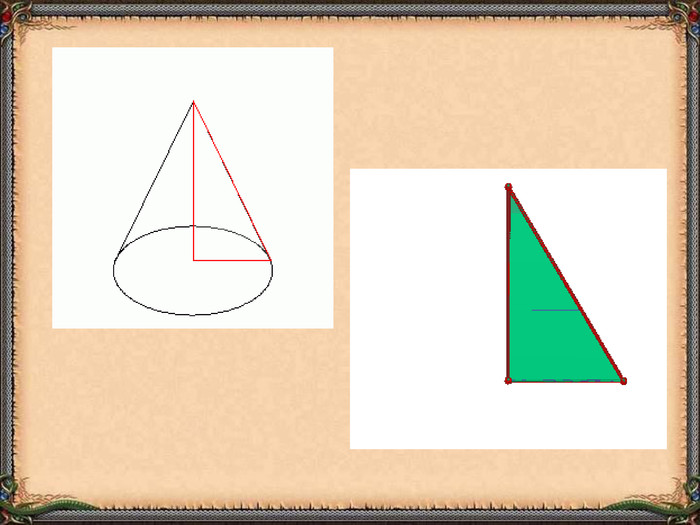
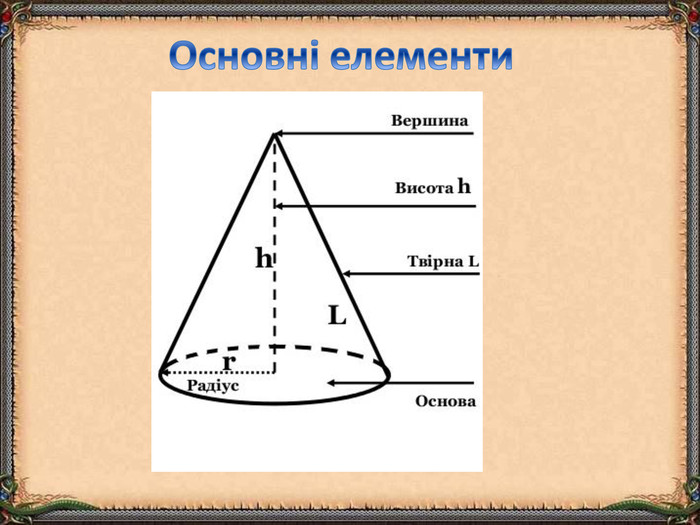
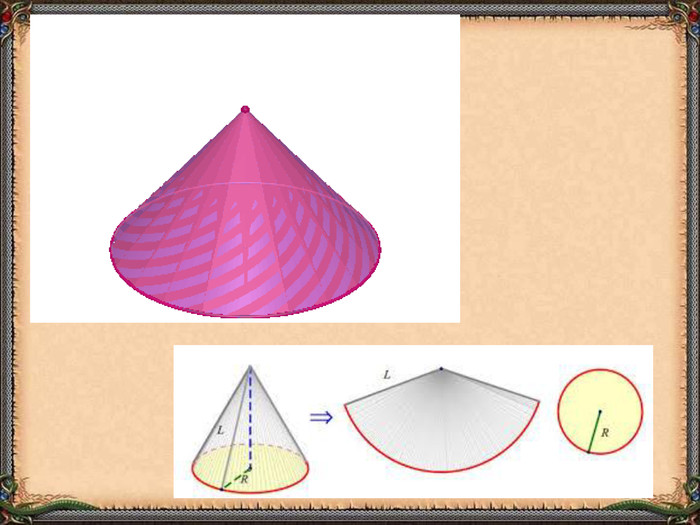
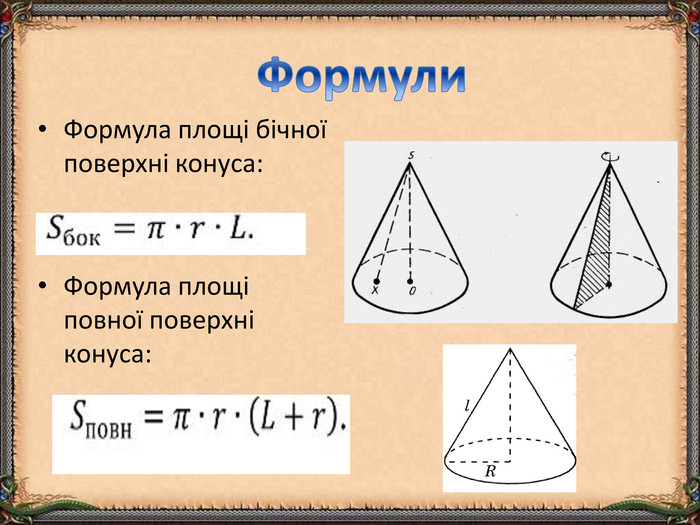
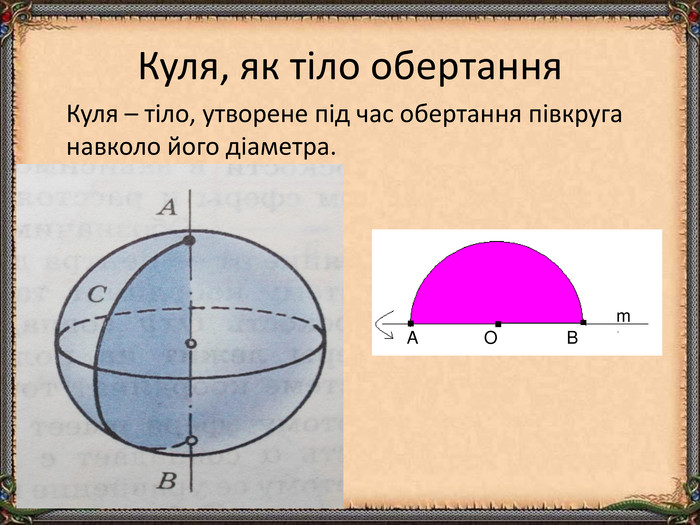
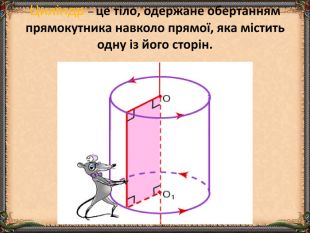
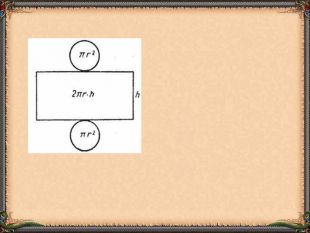
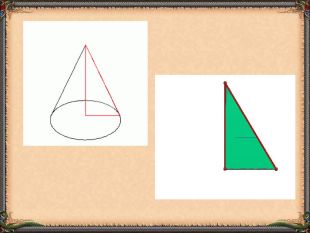
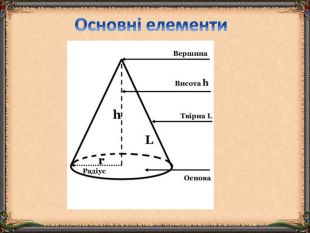
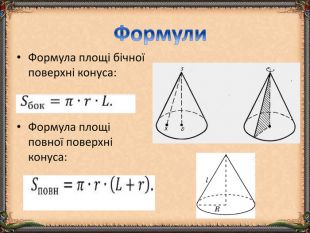
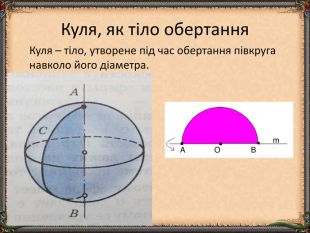
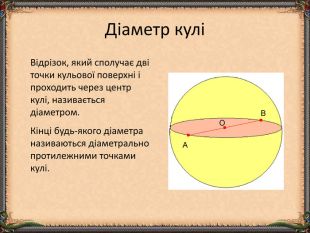
Презентація "Циліндр. Конус. Куля." (математика, 6 клас) містить приклади тіл обертання в навколишньому середовищі, зображень, формул площ бічних поверхонь.
6 клас Підгірненська ЗОШ І-ІІІ ступенів 2018
Для прокатки білизни в Древній Греції жінки застосовували скалку, яку по-грецьки називали «календер». Тому всі витягнуті тіла з округлим перерізом одержали назву циліндра.
Циліндр – це тіло, одержане обертанням прямокутника навколо прямої, яка містить одну із його сторін.
А1 В1 О1 О А В О ВІСЬ ЦИЛІНДРА ОСНОВА ЦИЛІНДРА твірна РАДІУС ВИСОТА ЦИЛІНДРА Основи циліндра – рівні і лежать в паралельних площинах Твірні циліндра паралельні і рівні
Формула площі бічної поверхні конуса: Формула площі повної поверхні конуса:
Слово ’’куля’’ і ’’сфера’’ походять від грецького слова ’’сфайра’’- м’яч.
Куля, як тіло обертання Куля – тіло, утворене під час обертання півкруга навколо його діаметра. m A B O
Куля Кулею називається тіло, що складається з усіх точок простору, які знаходяться від даної точки на відстані, не більшій за дану. Ця точка називається центром кулі, а дана відстань радіусом кулі.
Діаметр кулі Відрізок, який сполучає дві точки кульової поверхні і проходить через центр кулі, називається діаметром. Кінці будь-якого діаметра називаються діаметрально протилежними точками кулі. А В О
Сфера Межа кулі називається кульовою поверхнею або сферою. Точками сфери є всі точки кулі, які віддалені від центра на відстань, що дорівнює радіусу. Площа сфери обчислюється за формулою: де r — радіус сфери.
До зустрічі! Підгірне
про публікацію авторської розробки
Додати розробку
-
Яценко Людмила Петрівна
24.01.2023 в 15:38
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-
Наркевич Ірина
11.12.2022 в 22:17
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-
Ковтун Тетяна Петрівна
05.04.2021 в 23:04
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-
Volchkova Maria Ivanivna
20.01.2021 в 19:10
Хороша презентація. Матеріал подано повно, з намаганням задіяти просторову уяву учнів.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 1 відгук